¡Bienvenidos a nuestros ejercicios interactivos de Movimiento Rectilíneo Uniformemente Acelerado! El Movimiento Rectilíneo Uniformemente acelerado (MRUA) es un tipo de movimiento en el que un objeto se desplaza en línea recta con aceleración constante.
Los ejercicios que encontrarás a continuación te permitirán aplicar y consolidar tus conocimientos sobre el MRUA, desde la interpretación de gráficas hasta la resolución de problemas prácticos. Prepárate para poner en práctica tus habilidades matemáticas y conceptuales, ya que cada ejercicio te desafiará a aplicar fórmulas específicas y a comprender los principios detrás del MRUA.
Empleando la grafica de la aceleración con respecto al tiempo de una partícula, responde las siguientes tres preguntas:
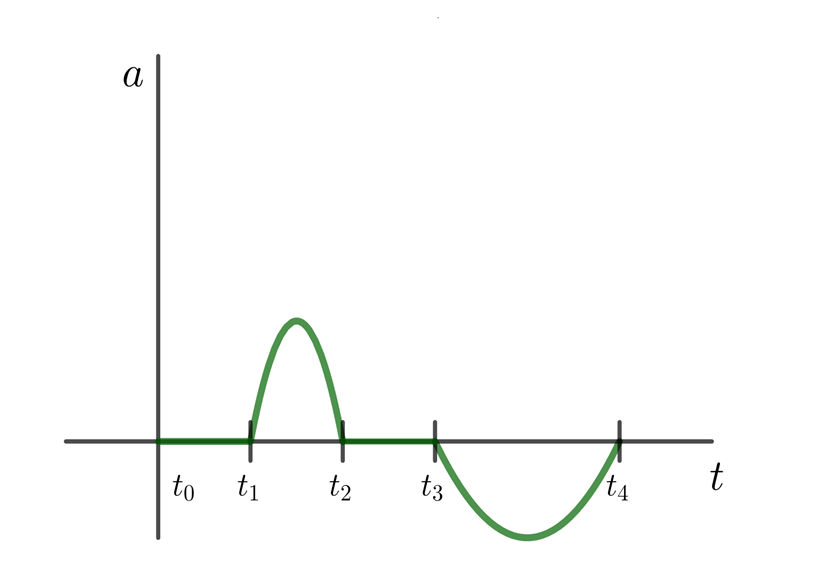
1 En los intervalos de tiempo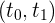 
y 
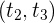, la velocidad...
1 Notamos que en ambos intervalos de tiempo la aceleración es cero, lo cual indica que la velocidad es constante.
2En el intervalo intermedio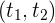 
la aceleración es positiva y la velocidad incrementa respecto a la velocidad en el intervalo .
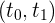3 Al llegar al intervalo 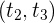, la aceleración de la partícula es cero, por lo que su velocidad deja de incrementar y permanece constante, pero es mayor a la velocidad en .
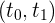2En el intervalo de tiempo 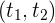, la velocidad...
1 Notamos que en el intervalo de tiempo 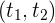la aceleración es positiva, lo cual indica que la velocidad va aumentando en cada unidad de tiempo
3En el intervalo de tiempo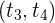 
, la partícula...
1 Notamos que en el intervalo de tiempo 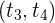la aceleración es negativa, lo cual indica que la velocidad va disminuyendo por cada unidad de tiempo
4 Una velocista parte de la línea de salida y se mueve en línea recta acelerando hasta alcanzar una velocidad de 30 kilómetros por hora en 10 segundos. ¿Cuál es la aceleración promedio de la velocista?
1 Identificamos los datos conocidos
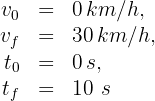
2Verificamos que se tengan las mismas unidades. Notamos que la velocidad está dada en kilómetros por hora y el tiempo empleado en segundos, entonces convertimos la velocidad a metros por segundos
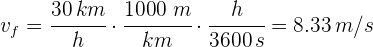
3Sustituimos en la ecuación de aceleración promedio
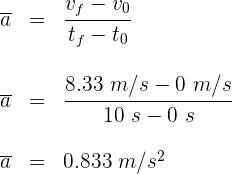
5Un maratonista cruza la línea de meta a una velocidad de 10 kilómetros por hora y comienza a desacelerar hasta alcanzar una velocidad de 2 kilómetros por hora en 5 segundos. ¿Cuál es la aceleración promedio del maratonista?
1 Identificamos los datos conocidos
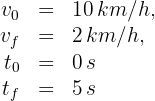
2Verificamos que se tengan las mismas unidades. Notamos que la velocidad está dada en kilómetros por hora y los resultados en metros por segundos al cuadrado, entonces la convertimos a estas unidades
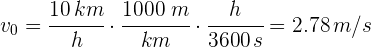
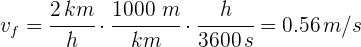
3Sustituimos en la ecuación de aceleración promedio
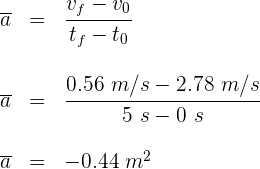
6Una partícula que va a 5 m/s se detiene en 2 s. Si su aceleración es constante, cuál es su valor?
1Identificamos los datos conocidos
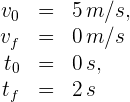
2Sabemos que la aceleración es constante, por lo que empleamos la fórmula de aceleración constante
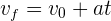
3Sustituimos y obtenemos
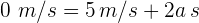
4Así, la aceleración constante es
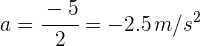
7Una partícula se mueve a una velocidad de 5 metros por segundo. Si su aceleración es constante y al cabo de 4 segundos su velocidad es 8 metros por segundo, ¿cuál es la velocidad promedio de la partícula?
1 Como la aceleración es constante, la velocidad promedio es igual al promedio de la velocidad inicial y final en cualquier intervalo de tiempo
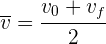
2 Sustituimos los valores de las velocidades final e inicial para obtener
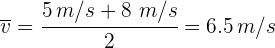
8Una persona se mueve en línea recta con una aceleración constante de 3 metros por segundo al cuadrado. Si la velocidad inicial es de 4 metros por segundo. ¿Cuál es su desplazamiento después de 20 segundos?
1Identificamos los datos conocidos
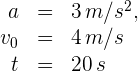
2 Con los datos anteriores podemos encontrar la posición final al cabo de 20 segundos. Como la aceleración es constante, empleamos la fórmula
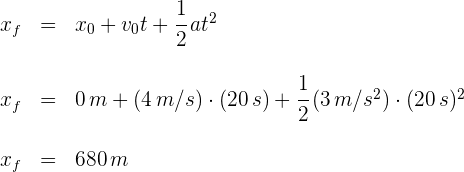
El desplazamiento viene dado por
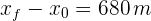
9Un automóvil se desplaza en línea recta una distancia de 30 kilómetros, iniciando a 50 km/h y terminando a 80 km/h. Si la aceleración es constante, ¿cuánto tiempo le lleva recorrer los 30 kilómetros?
1Identificamos los datos conocidos
2 Como la aceleración es constante, empleamos la fórmula
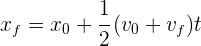
3 Sustituimos los datos conocidos y despejamos el tiempo
10Un automóvil con velocidad de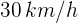 
tiene una aceleración constante de 
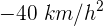. ¿Cuál es el desplazamiento del automóvil hasta detenerse?
1Identificamos los datos conocidos
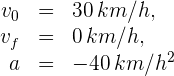
2 Como la aceleración es constante, empleamos la fórmula
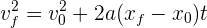
3 Sustituimos los datos conocidos y despejamos el desplazamiento 
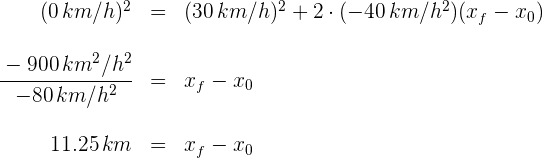
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Hola buenas. Tengo una corrección respecto al ejercicio 5. La aceleración fue calculada de forma correcta, sin embargo, al calcular la distancia se debe utilizar la ecuación de itinerario de la posición, en concreto:
X = Xo + Vo • t + (1/2) • a • t^2
Al utilizar esta ecuación, se considera el movimiento acelerado para el desplazamiento del automóvil, en t = 2 [h]. Al utilizar la ecuación que pusiste en la solución, consideras como velocidad final, los 75 [km/h], en lugar de la velocidad alcanzada realmente en t = 2[h], la cual se puede calcular utilizando la ecuación de velocidad.
V = Vo + a • t
Con t= 2 [h], esa V te da un valor de 45 [km/h]. Al utilizar ese valor en la ecuación que tu planteaste, te da el desplazamiento real, el cual te da un valor de 70 [km], lo cual también se obtiene con la ecuación de itinerario de posición:
X = Vo • t + (1/2) • a • t^2
X = (25 • 2) + ((1/2) • (10 • 2^2)) [km]
X = 70 [km]
Hola tienes razón, una disculpa ya se corrigió.
8. Dos vehículos salen al encuentro desde dos ciudades separadas por 300 km, con
velocidades de 60 km/h y 40 km/h, respectivamente. Si el que circula a 40 km/h sale dos
horas más tarde, responda a las siguientes preguntas: a) El tiempo que tardan en encontrarse.
b) La posición donde se encuentran.
En el problema siete está mal la unidad de medida de la aceleración, está se mide en m/s^2 no en m^2
Hola, una disculpa por el error ya se corrigió.
5.- Dos motocicletas están separadas una distancia de 2 km. La primera se mueve a
velocidad (constante) de 25 m·s-1. La segunda, parte de parado con una aceleración
constante de 3 m·s-2. Calcule:
a) Cuanto tiempo tardarán en encontrase, si una va en dirección opuesta a la otra.
b) Si las dos van en la misma dirección, ¿cuánto tiempo tardará la segunda
moticicleta en pillar a la primera?
c) En este último caso, ¿en qué punto la pillará?
Trayectoria de un objeto lanzado
Un balón es llazando ª 30
Con una velocidad inicial de 15 m/s graficar su trayectoria en el plano Xy usando geogebra o tracker