¡Bienvenidos al fascinante mundo del movimiento rectilíneo uniformemente acelerado (MRUA)! En este conjunto de ejercicios, exploraremos uno de los conceptos fundamentales de la cinemática, donde los objetos se desplazan a lo largo de una línea recta con una aceleración constante.
A través de estos ejercicios, profundizaremos en la comprensión de las ecuaciones y conceptos clave que describen el MRUA, como la posición, la velocidad y la aceleración en función del tiempo. Estos problemas te desafiarán a aplicar fórmulas específicas, comprender relaciones matemáticas y visualizar el comportamiento de los objetos en movimiento.
Una partícula parte del reposo y se mueve en línea recta acelerando hasta alcanzar una velocidad de 10 metros por segundo en un tiempo de 10 segundos. ¿Cuál es la aceleración promedio de la partícula? Si la aceleración es constante, ¿cuál es el valor de esta?
1 Identificamos los datos conocidos
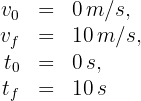
2Sustituimos en la ecuación de aceleración promedio
Así, la aceleración promedio es de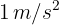 
.
3Para encontrar la aceleración constante, sustituimos en la ecuación de aceleración constante
Así, la aceleración es de 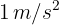, que es igual a la aceleración promedio.
Un ciclista se mueve en línea recta con una velocidad de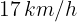 
. Si aumenta su velocidad con una aceleración de 
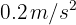durante 10 segundos ¿Cuál es su desplazamiento en los 10 segundos?
1 Identificamos los datos conocidos
2Verificamos que se tengan las mismas unidades. Notamos que la velocidad inicial está dada en kilómetros por hora, entonces la convertimos a metros por segundo
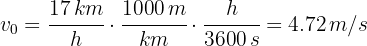
3Recordamos que el desplazamiento es igual a la diferencia de la posición final con la inicial 
. Dado que conocemos la aceleración la cual es constante, la velocidad inicial y el tiempo empleado, entonces utilizamos la fórmula
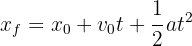
4Despejamos la fórmula para obtener el desplazamiento y sustituimos en la ecuación los datos conocidos
Así, el ciclista recorre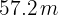 
.
Un automóvil va a ingresar a una zona escolar, por lo que disminuye su velocidad de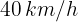 
a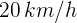 
. Si tarda 5 segundos en realizarlo, ¿cuál es su desaceleración?
1 Identificamos los datos conocidos:
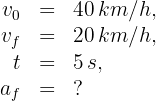
2Verificamos que se tengan las mismas unidades. Notamos que la velocidad inicial y final están dadas en kilómetros por hora, entonces las convertimos a metros por segundo
3Sustituimos en la fórmula de aceleración constante
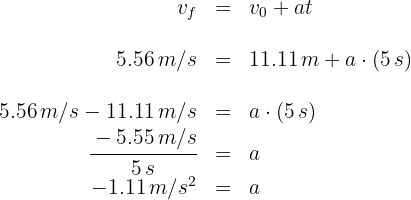
Así, el automóvil tiene una desaceleración de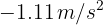 
.
Un tren de alta velocidad viaja a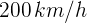 
y desacelera de manera constante a razón de 
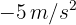hasta detenerse. ¿Cuánto tiempo emplea en realizarlo?
1 Como el tren desacelera de forma constante, se trata de un problema de movimiento rectilíneo uniformente acelerado.
2 Identificamos los datos conocidos:
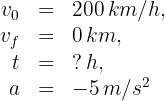
3Verificamos que se tengan las mismas unidades. Notamos que la velocidad inicial y final están dadas en kilómetros por hora y la aceleración en metros por segundos al cuadrado, entonces convertimos las velocidades a metros por segundo
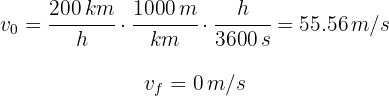
3Sustituimos en la fórmula de aceleración constante
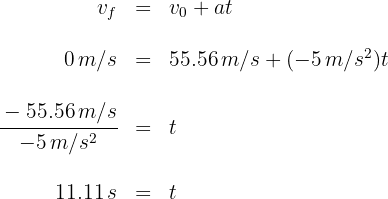
Así, el tren tarda en detenerse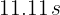 
.
La velocidad de un automóvil con respecto al tiempo se representa en la siguiente gráfica
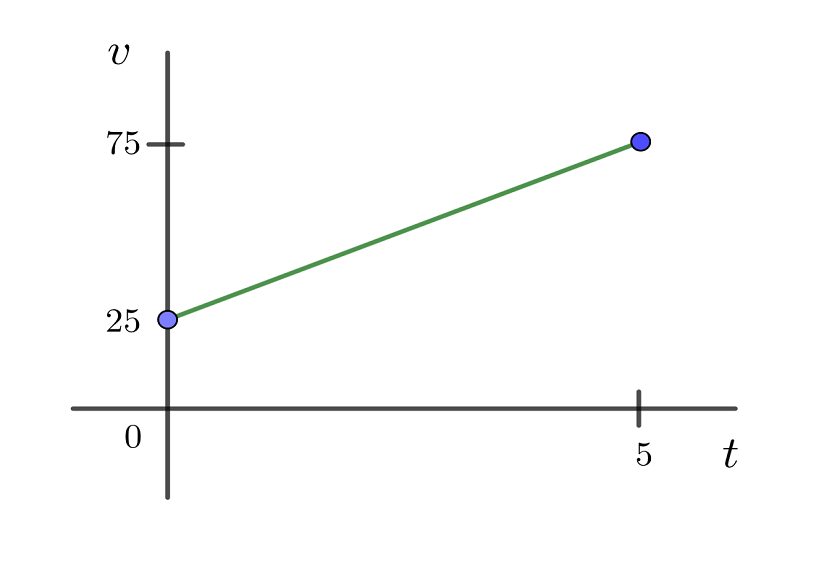
Si la velocidad está dada en kilómetros por hora y el tiempo en horas, ¿cuál es la aceleración del automóvil y que distancia recorre en 2 horas?
1 De la gráfica observamos que se trata de una recta, por lo que estamos ante el caso de un problema de aceleración constante
2 Al tratarse de aceleración constante, esta es igual a la pendiente de la recta
3 Para encontrar la distancia recorrida en 2 horas y sabiendo que la aceleración es constante, empleamos la fórmula
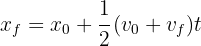
4Sustituimos los datos de la gráfica
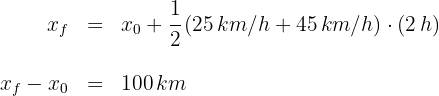
Así, el automóvil recorre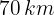 
en 2 horas.
La función de velocidad en metros por segundo de una persona se representa en la siguiente gráfica
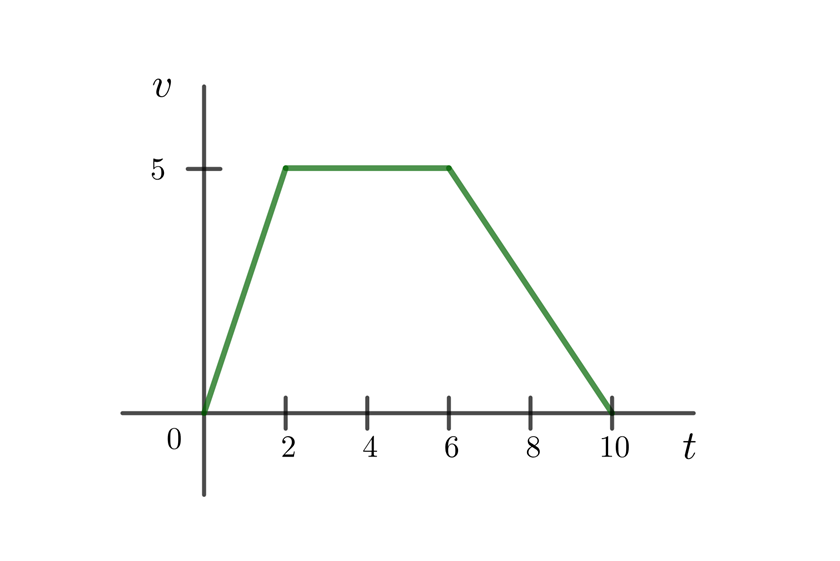
Si el tiempo se mide en segundos, ¿cuál es la aceleración de la persona en los distintos intervalos de tiempo?
1 De la gráfica observamos que la función de velocidad respecto al tiempo son rectas en intervalos, por lo que es un problema de movimiento rectilíneo uniformemente acelerado y la aceleración es igual a la pendiente de la recta en dichos intervalos
2 En el intervalo de tiempo de 0 a 2 segundos, la aceleración constante es
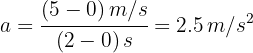
3 En el intervalo de 2 a 6 segundos la velocidad permanece constante, por lo que la aceleración es cero
4 En el intervalo de tiempo de 6 a 10 segundos, la aceleración constante es negativa
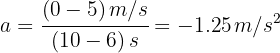
Dos partículas se encuentran en la misma posición. La primera se mueve a velocidad constante de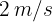 
y después de avanzar 
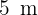, la segunda comienza a moverse del reposo con una aceleración de 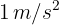. ¿Cuánto tiempo le llevará a la segunda partícula alcanzar a la primera?
1 Denotamos por 
a la distancia recorrida por la primera partícula hasta encontrarse con la segunda, por lo que la segunda partícula recorre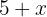 
en un mismo tiempo 
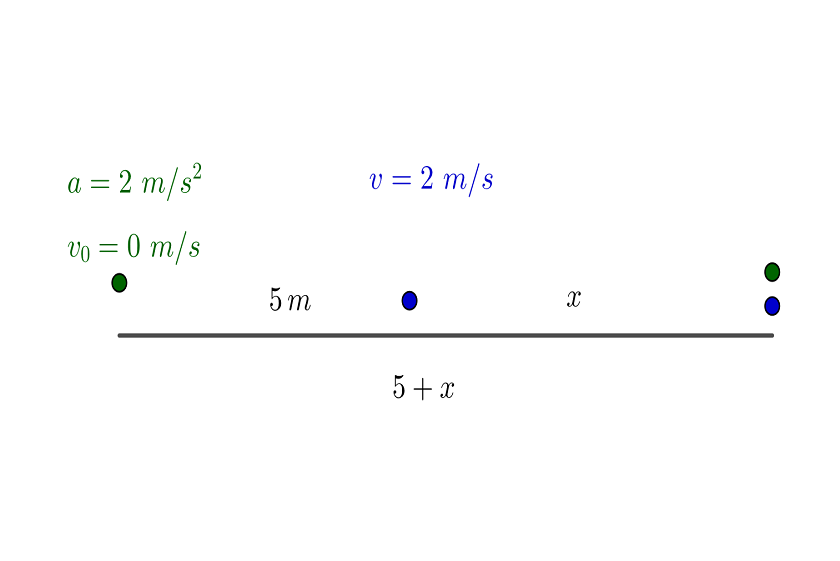
2 Como la primera partícula se mueve con velocidad constante, se tiene que
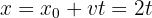
3 Como la segunda partícula se mueve con aceleración constante y comienza en el reposo, se tiene que
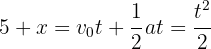
4 Sustituimos el valor de de la primera ecuación en la segunda y resolvemos
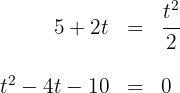
5 Resolvemos empleando la fórmula general cuadrática y obtenemos
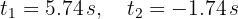
6Tomamos el tiempo positivo, ya que el negativo no tiene sentido en este problema. Así, ambas partículas se encuentran a los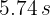 
Un automóvil con velocidad de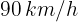 
desacelera a razón de 
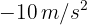hasta que su velocidad es igual a 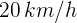. ¿Cuál es el desplazamiento del automóvil?
1 Identificamos los datos conocidos:
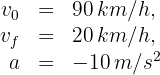
2Verificamos que se tengan las mismas unidades. Notamos que la velocidad inicial y final están dadas en kilómetros por hora, entonces las convertimos a metros por segundo
3 Utilizamos la fórmula para aceleración constante
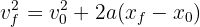
4 Sustituimos los datos y despejamos el desplazamiento
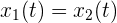
4Igualamos ambas funciones de velocidad constante y despejamos el tiempo
Así, el automóvil se desplaza 29.7 metros.
Una persona que camina a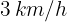 
pasa por un punto A; 5 minutos después una segunda persona pasa por el punto A a 
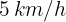. Si ambas personas se mueven con aceleraciones constantes de 
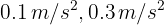respectivamente, ¿cuánto tiempo habrá transcurrido hasta que ambas se encuentren?
1 Identificamos los datos conocidos:
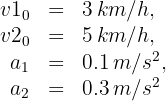
2Verificamos que se tengan las mismas unidades. Notamos que las velocidades iniciales están dadas en kilómetros por hora, entonces las convertimos a metros por segundo. También transformamos los minutos a segundos
3 Como ambos se mueven con aceleración constante, usamos la fórmula
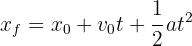
4 Si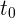 
es el tiempo que tarda la segunda persona en alcanzar a la primera, esta habrá empleado 300 segundos más que la segunda, por lo que tenemos para la segunda persona
La primera persona se encuentra en las misma posiciones en el tiempo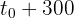 
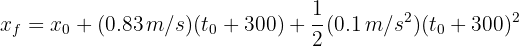
5Igualamos los desplazamientos
6Resolvemos empleando la fórmula general cuadrática para obtener
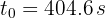
Así, ambas personas se encuentran después de 404.6 segundos, que es lo mismo que 6.74 minutos.
Dos partículas se encuentran separadas 10 metros entre si. Si ambas parten del reposo con aceleraciones de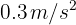 
y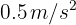 
, ¿cuánto tiempo habrá transcurrido hasta que ambas se encuentren?
1 Conviene representar gráficamente el problema. Para ello tenemos que establecer la dirección del movimiento siendo la positiva la dirección de la primera partícula y negativa la de la segunda, de manera que ambas se encuentran en los extremos opuestos, a tiempo cero. La distancia recorrida por la primera partícula es y la de la segunda es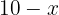 
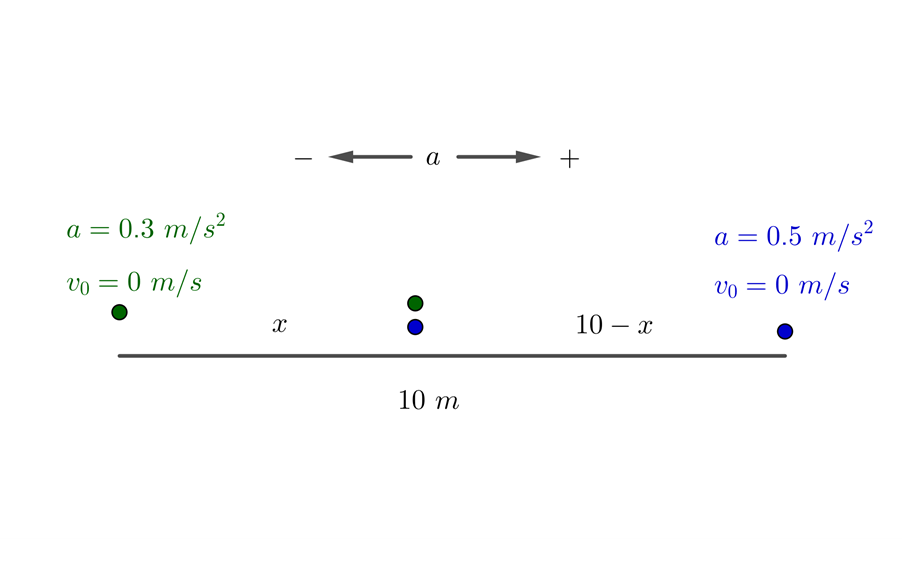
2 Como ambos se mueven con aceleración constante, empleamos la fórmula
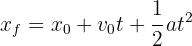
El desplazamiento de la primera partícula es
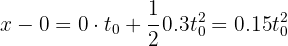
El desplazamiento de la segunda partícula es, empleando la dirección de la aceleración
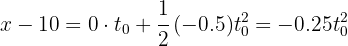
3 Como el tiempo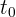 
recorrido por ambas partículas hasta encontrarse es el mismo, tenemos
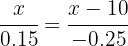
4Despejando, obtenemos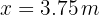 
. Sustituimos la función de tiempo para obtener
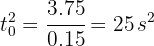
Así, ambas partículas se encuentran a los 5 segundos
Si tienes dudas, aquí puedes consultar la teoría.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Hola buenas. Tengo una corrección respecto al ejercicio 5. La aceleración fue calculada de forma correcta, sin embargo, al calcular la distancia se debe utilizar la ecuación de itinerario de la posición, en concreto:
X = Xo + Vo • t + (1/2) • a • t^2
Al utilizar esta ecuación, se considera el movimiento acelerado para el desplazamiento del automóvil, en t = 2 [h]. Al utilizar la ecuación que pusiste en la solución, consideras como velocidad final, los 75 [km/h], en lugar de la velocidad alcanzada realmente en t = 2[h], la cual se puede calcular utilizando la ecuación de velocidad.
V = Vo + a • t
Con t= 2 [h], esa V te da un valor de 45 [km/h]. Al utilizar ese valor en la ecuación que tu planteaste, te da el desplazamiento real, el cual te da un valor de 70 [km], lo cual también se obtiene con la ecuación de itinerario de posición:
X = Vo • t + (1/2) • a • t^2
X = (25 • 2) + ((1/2) • (10 • 2^2)) [km]
X = 70 [km]
Hola tienes razón, una disculpa ya se corrigió.
8. Dos vehículos salen al encuentro desde dos ciudades separadas por 300 km, con
velocidades de 60 km/h y 40 km/h, respectivamente. Si el que circula a 40 km/h sale dos
horas más tarde, responda a las siguientes preguntas: a) El tiempo que tardan en encontrarse.
b) La posición donde se encuentran.
En el problema siete está mal la unidad de medida de la aceleración, está se mide en m/s^2 no en m^2
Hola, una disculpa por el error ya se corrigió.
5.- Dos motocicletas están separadas una distancia de 2 km. La primera se mueve a
velocidad (constante) de 25 m·s-1. La segunda, parte de parado con una aceleración
constante de 3 m·s-2. Calcule:
a) Cuanto tiempo tardarán en encontrase, si una va en dirección opuesta a la otra.
b) Si las dos van en la misma dirección, ¿cuánto tiempo tardará la segunda
moticicleta en pillar a la primera?
c) En este último caso, ¿en qué punto la pillará?
Trayectoria de un objeto lanzado
Un balón es llazando ª 30
Con una velocidad inicial de 15 m/s graficar su trayectoria en el plano Xy usando geogebra o tracker