La velocidad media es el cociente entre el espacio recorrido 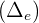 y el tiempo transcurrido
y el tiempo transcurrido 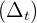 . Fisicamente esto lo podemos interpretar como el cambio de posición respecto al tiempo o como la pendiente de la recta que une el punto inicial y el punto final del recorrido.
. Fisicamente esto lo podemos interpretar como el cambio de posición respecto al tiempo o como la pendiente de la recta que une el punto inicial y el punto final del recorrido.
Si dado un tiempo  y una función
y una función 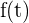 , queremos saber la velocidad media de ir de un punto
, queremos saber la velocidad media de ir de un punto 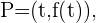 hasta un punto
hasta un punto 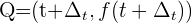 siguiendo el recorrido de la función
siguiendo el recorrido de la función 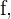 podemos utilizar la siguiente fórmula
podemos utilizar la siguiente fórmula
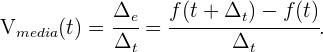
La fórmula anterior se puede deducir fácilmente a partir de la siguiente grafica.

Velocidad instantánea
La derivada de una función 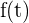 en un punto
en un punto  no es más que la velocidad en el instante
no es más que la velocidad en el instante 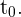 Este fenómeno también lo podemos interpretar como la pendiente de la recta tangente a la función
Este fenómeno también lo podemos interpretar como la pendiente de la recta tangente a la función 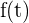 en el punto
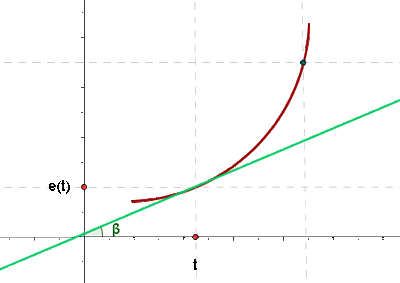
en el punto 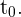 Podemos calcular la velocidad instantánea calculando el siguiente limite
Podemos calcular la velocidad instantánea calculando el siguiente limite

Cálculo de las velocidades media e instantánea
La relación entre la distancia recorrida en metros por un móvil y el tiempo en segundos es  . Calcular:
. Calcular:
1 La velocidad media entre 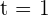 y
y  .
.
La velocidad media es el cociente incremental en el intervalo 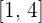 . De esta forma tenemos el siguiente valor para la velocidad media
. De esta forma tenemos el siguiente valor para la velocidad media

2 La velocidad instantánea en 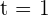 .
.
Recordemos que la velocidad instantánea es la derivada de la función 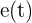 en el instante
en el instante 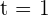 . Así que el resultado es
. Así que el resultado es
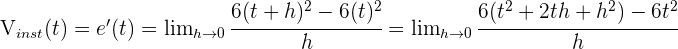
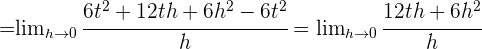

Resumir con IA:














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Quería solo advertir que el gráfico de la diferencial tiene el ángulo de la recta tangente con β y analíticamente está indicado con α. Saludos.
hola gracias por tu observación, pero si el artículo es de «interpretación de la derivada» es el mismo ángulo pero con símbolo diferente.
cordial saludo sera que tu me puedes ayudar a resolver un ejercicio que es dada la función f(x)= X elevada a la 2/3 por entre paréntesis (xa la 2 -8) hallar los valores de X para los cuales esta crece te lo agradecería mucho
La descripcion es erronea donde da la derivada de arcocotangente, ya que dice derivada de arcotangete, se comieron el co, lo que puede llevar a confunciones, como en mi caso que pense que era la derivada de la inversa de tangente, cuando era la derivada de la inversa de cotangente.
Hola entendemos la confusión, pero como sabes en cada lugar toman la notación en forma diferente, en este caso se tomo arccot(x) donde se repite la c para diferenciar de arctan(x).
me pueden ayudar encontrar la derivada de : y=7 elevado a la 4 + e elevado a la x-4 – ln X + 100
Medio tarde me parece mi respuesta, pero simplemente tenes que derivar cada termino independientemente:
7^4=(7.4)^3
e^x-4=e^x-4 (por formula)
lnx=1/x
100=0 (Derivando una constante en terminos de x)
Hola podrías hacernos el favor de mostrarnos la función para dar una mejor explicación.