Capítulos
- Clasificación de los vectores
- Coordenadas de un Vector
- Módulo de un vector
- Combinación lineal de vectores
- Sistema de referencia
- Bases
- Coordenadas del punto medio de un segmento
- Condición para qué tres puntos estén alineados
- Simétrico de un punto respecto de otro
- Coordenadas del baricentro
- División de un segmento en una relación dada
- Producto escalar
- Un vector fijo
es un segmento orientado que va del punto A (origen) al punto B (extremo). - Un vector fijo es nulo cuando el origen y su extremo coinciden.
- El módulo del vector es la longitud del segmento
. - El módulo se representa por .
- La direcccíon del vector es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella.
- El sentido del vector es el que va desde el origen
al extremo 
.
Clasificación de los vectores
1 Vectores equipolentes:
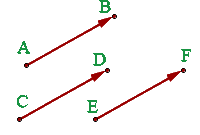
Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido.
2Vectores libres:
El conjunto de todos los vectores equipolentes entre sí se llama vector libre. Cada vector fijo es un representante del vector libre.
Coordenadas de un Vector
1 Vector de posición de un punto en el plano de coordenadas
El vector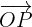 
que une el origen de coordenadas 
con un punto 
se llama vector de posición del punto .
2Coordenadas o componentes de un vector en el plano
Si las coordenadas de y son:
Las coordenadas o componentes del vector son las coordenadas del extremo menos las coordenadas del origen.
Módulo de un vector
El módulo de un vector es la longitud del segmento orientado que lo define.
El módulo de un vector es un número siempre positivo y solamente el vector nulo tiene módulo cero.
Cálculo del módulo conociendo sus componentes
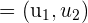
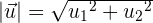
Cálculo del módulo conociendo las coordenadas de los puntos
Distancia entre dos puntos
La distancia entre dos puntos es igual al módulo del vector que tiene de extremos dichos puntos.
Módulo la unidad
Los vectores unitarios tienen de módulo la unidad.
Suma de vectores
Para sumar dos vectores libres 
y 
se escogen como representantes dos vectores tales que el extremo de uno coincida con el origen del otro vector.
Regla del paralelogramo
Se toman como representantes dos vectores con el origen en común, se trazan rectas paralelas a los vectores obteniéndose un paralelogramo cuya diagonal coincide con la suma de los vectores.
Para sumar dos vectores se suman sus respectivas componentes.
Resta de vectores
Para restar dos vectores libres y se suma con el opuesto de .
Las componentes del vector resta se obtienen restando las componentes de los vectores.
Producto de un número por un vector
El producto de un número 
por un vector es otro vector:
1 De igual dirección que el vector .
2 Del mismo sentido que el vector si es positivo.
3 De sentido contrario del vector si es negativo.
4 De módulo 
Las componentes del vector resultante se obtienen multiplicando por las componentes del vector.
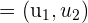
Combinación lineal de vectores
Dados dos vectores: y , y dos números: 
y 
, el vector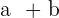 
se dice que es una combinación lineal de y .
Cualquier vector se puede poner como combinación lineal de otros dos que tengan distinta dirección.
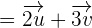
Esta combinación lineal es única.
Sistema de referencia
En el plano, un sistema de referencia está constituido por un punto del plano y una base ( , ).
El punto del sistema de referencia se llama origen.
Los vectores , no paralelos forman la base.
Bases
1Ortogonal
Los vectores base son perpendiculares, pero de distinto módulo.
2 Ortonormal
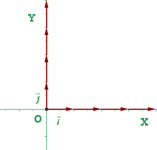
Los vectores de la base son perpendiculares y unitarios, es decir, de módulo 
.
Se representan por las letras 
.
.
.
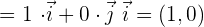Las rectas 
, 
se llaman ejes de coordenadas o ejes coordenados cartesianos.
Coordenadas del punto medio de un segmento
Las coordenadas del punto medio de un segmento son la semisuma de las coordenadas de los extremos.
Condición para qué tres puntos estén alineados
Los puntos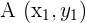 
, 
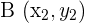y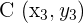 
están alineados siempre que los vectores y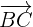 
tengan la misma dirección. Esto ocurre cuando sus coordenadas son proporcionales.
Simétrico de un punto respecto de otro
Si 
es el simétrico de respecto de 
, entonces es el punto medio del segmento 
. Por lo que se verificará igualdad:
Coordenadas del baricentro
Baricentro o centro de gravedad de un triángulo es el punto de intersección de sus medianas.
Las coordenadas del baricentro son:
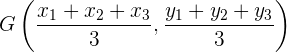
División de un segmento en una relación dada
Dividir un segmento en una relación dada 
es determinar un punto de la recta que contiene al segmento , de modo que las dos partes,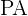 
y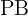 
, están en la relación :
Producto escalar
El producto escalar de dos vectores es un número real que resulta al multiplicar el producto de sus módulos por el coseno del ángulo que forman.
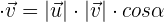
1Expresión analítica del producto escalar
2Expresión analítica del módulo de un vector
3 Expresión analítica del ángulo de dos vectores
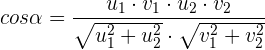
4 Condición analítica de la ortogonalidad de dos vectores
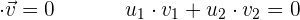
Proyección
El producto de dos vectores no nulos es igual al módulo de uno de ellos por la proyección del otro sobre él.
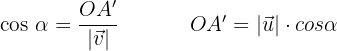
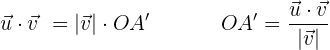
Propiedades del producto escalar
1 Conmutativa
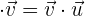
2 Asociativa
3 Distributiva
4 El producto escalar de un vector no nulo por sí mismo siempre es positivo.
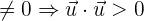
Si necesitas ayuda personalizada para entender los vectores, puedes encontrar tu profesor ideal para un curso de matematicas adaptado a tus necesidades.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Suma de vectores f1=450n,30. 1FR=f1+f6
como sacar el residuo de una multiplicación
Hallar las coordenadas de punto medio del segmento que une (4,7);(14,12)
Hola, podrias mencionar que tipo de multiplicación (normal, de vectores etc.).
si se aplica una traslación al punto E(0;2) se obtiene el punto E'(-1;-5),indicar el vector de translación
Traslaciones Juan es un diseñador gráfico y de acuerdo con las exigencias de uno de sus clientes debe reorganizar los elementos de uno de los avisos publicitarios observemos en la ilustración los cambios y desplazamientos que realizo.
En la ilustración el barco se trasladó dos unidades hacia arriba.
Una traslación es el desplazamiento de una figura sobre un plano sin girarla en ninguna dirección para indicar una traslación usamos una flecha que muestra el sentido hacia donde se hace el movimiento:
Derecha , izquierda, arriba, abajo, occidente, Oriente, Norte o sur) y la magnitud (número de unidades que se mueve la figura).
En el aviso publicitario,? Cuál de los siguientes desplazamientos se realizó con el logo del pez? Márcalo con x
Vectores 400n+horizontal y a la izquierda