¡Bienvenido al fascinante mundo de las vibraciones y ondas! Este conjunto de ejercicios interactivos está diseñado para ayudarte a explorar y comprender los conceptos fundamentales de estas áreas clave de la física. A lo largo de estos ejercicios, tendrás la oportunidad de experimentar con actividades prácticas que te permitirán visualizar y analizar los fenómenos de vibración y propagación de ondas.
Esperamos que estos ejercicios te proporcionen una comprensión sólida y una apreciación más profunda de las vibraciones y las ondas. ¡Disfruta del viaje interactivo y descubre la física en acción!
El sonar de un barco envía verticalmente hacia el fondo del mar un pulso de ultrasonidos. Si la velocidad del sonido en el agua es 1450 m/s y el fondo del mar se encuentra a 350 metros, entonces el tiempo empleado por el pulso para regresar al barco es...
Selecciona una respuesta.
1 Los datos que conocemos son:
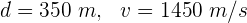
2 Empleamos la fórmula para la velocidad
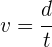
3 Sustituimos los datos que conocemos para obtener el tiempo que tarda el pulso en llegar al fondo marino
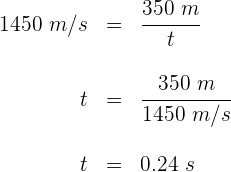
4 El tiempo encontrado corresponde al de ida, por lo que el tiempo requerido para que el pulso regrese al barco es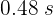 
Un bote anclado flota efectuando 15 oscilaciones completas en 8 segundos. La frecuencia de la onda es ...
Selecciona una respuesta.
1 Calculamos la frecuencia, para ello empleamos los datos de el número de oscilaciones completas y el tiempo en que se realiza
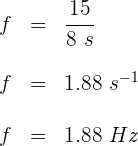
La cresta de la ola recorre el bote anclado de 20 metros en 6 segundos. La velocidad de la onda es...
Selecciona una respuesta.
1 Primero calculamos la velocidad de la onda, para ello los datos que conocemos son:
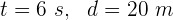
2 Empleamos la fórmula para la velocidad
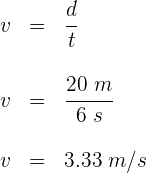
Un bote anclado flota efectuando 18 oscilaciones completas en 12 segundos y la cresta de la ola recorre el bote de 25 metros en 10 segundos. El número de ondas completas que existen en cualquier instante a lo largo de la longitud del bote es...
Selecciona una respuesta.
1 Primero calculamos la velocidad de la onda, para ello los datos que conocemos son:
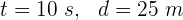
2 Empleamos la fórmula para la velocidad
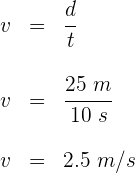
3 Calculamos la frecuencia, para ello empleamos los datos de el número de oscilaciones completas y el tiempo en que se realiza
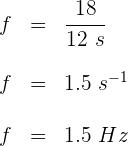
4 Conociendo la velocidad y la frecuencia de la onda, podemos calcular su longitud
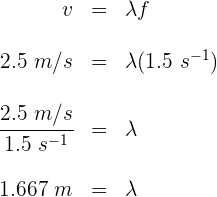
5 Para conocer el número de ondas a lo largo del bote, dividimos la longitud del mismo entre la longitud de onda
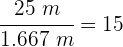
Durante un tsunami, a profundidades entre 4 y 5 kilómetros, las olas viajan a 600 km/h con longitud de onda de 100 kilómetros. La frecuencia de la onda producida por la cadena de olas es...
Selecciona una respuesta.
1Conociendo la velocidad y la longitud de la onda, podemos calcular su frecuencia
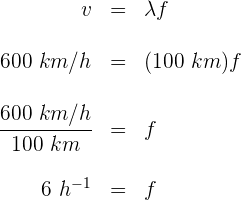
2 Convertimos las horas a segundos
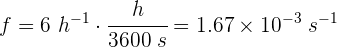
Observa que también puedes convertir primero las velocidades a m/s y al calcular la frecuencia las obtendrías en Hz
Las ondas transversales producidas por un terremoto tardan 110 segundos en ser detectadas en la estación de monitoreo. Si la velocidad de las ondas es de 4695 m/s la distancia a la que se produjo el terremoto es...
Selecciona una respuesta.
1 Los datos que conocemos son:
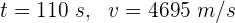
2 Empleamos la fórmula para la velocidad
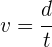
3 Sustituimos los datos que conocemos para obtener la distancia
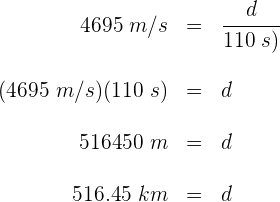
Un terremoto produce ondas transversales que tardan 95 segundos en ser detectadas por una estación de monitoreo que se encuentra a 537 kilómetros del origen del terremoto. La velocidad de las ondas es ...
Selecciona una respuesta.
1 Los datos que conocemos son:
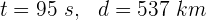
2 Empleamos la fórmula para la velocidad
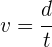
3 Sustituimos los datos que conocemos
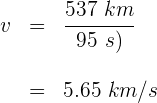
Un terremoto produce ondas primarias que viajan a 7.62 km/s y ondas secundarias que se mueven a 4.81 km/s. Si el tiempo de llegada de las dos ondas a la estación de monitoreo tiene un retraso de 42 segundos, el tiempo le tomó a las ondas secundarias llegar desde el origen del terremoto hasta la estación sísmica es...
Selecciona una respuesta.
1 Si 
es el tiempo que tarda en llegar la onda primaria, los datos que conocemos son:
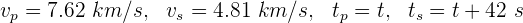
2 Empleamos la fórmula para la velocidad de ambas ondas
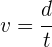
3 Sustituimos los datos que conocemos para obtener la distancia para cada una de las ondas
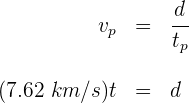
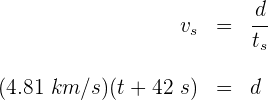
4 Como ambas ondas recorren la misma distancia, las igualamos y despejamos el tiempo
5 Así, el tiempo que tarda la onda secundaria es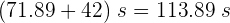 
Un terremoto produce ondas primarias y ondas secundarias, teniendo estas últimas una velocidad de 5.2 km/s y llegan a la estación de monitoreo 39 segundos después de que llegan las ondas primarias. Si el terremoto se originó a 530 kilómetros de la estación de monitoreo, el tiempo en que llegan las ondas primarias a la estación de monitoreo es...
Selecciona una respuesta.
1 Conocemos la distancia que recorren las ondas secundarias y su velocidad, por lo que calculamos el tiempo empleado desde su origen hasta la estación de monitoreo
2 El tiempo de retraso de las ondas secundarias es de 39 segundos , luego el tiempo de las ondas primarias es de 62.92 segundos.
Un terremoto produce ondas primarias que viajan a 6.5 km/s y ondas secundarias que se mueven a 4.2 km/s. Si el tiempo de llegada de las dos ondas a la estación de monitoreo tiene un retraso de 45 segundos, la distancia del origen del terremoto a la estación sísmica es...
Selecciona una respuesta.
1 Si es el tiempo que tarda en llegar la onda primaria, los datos que conocemos son:
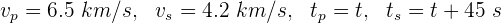
2 Empleamos la fórmula para la velocidad de ambas ondas
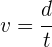
3 Sustituimos los datos que conocemos para obtener la distancia para cada una de las ondas
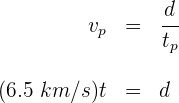
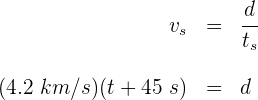
4 Como ambas ondas recorren la misma distancia, las igualamos y despejamos el tiempo
5 La distancia buscada es
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Hola, muchas gracias por compartir estos ejercicios. Me parece que en el ejercicio 3 la respuesta es 2.5Hz y no 0.25Hz. Saludos
La respuesta correcta es 2,5 HZ
Hola te agradecemos tu observación, una disculpa y ya se corrigió.
Holiii. Super buenos ejercicios, pero la tres está mal, pues 1÷0.4s es 2.5hz, no 0.25
Hola te agradecemos tus observaciones y una disculpa, ya se corrigió.
Corrígeme si me equivoco, pero en el 8 el recorrido sería la mitad (600m) , puesto que tarda 1s en llegar al fondo del lago y otro segundo en volver y ser recibida. Un saludo
Hola, me encantaría poder resolver tu dudad, pero necesito que me digas de que tema es tu ejercicio, pues a mi me señala que es un ejercicio de ondas aplicado a un tren de carga y tu mencionas un lago, lo cual me crea dificultades.
La nota musical tiene una frecuencia de 440Hz y tiene una velocidad de 340 m/s en el aire . Calcula su longitud
la 1 esta mal
Hola, disculpa pero podrías señalar porque esta mal, pues no encontré el error.