El principio de superposición es un concepto fundamental en física que nos permite entender cómo se combinan y afectan entre sí las ondas cuando se encuentran en el mismo medio.
Según este principio, cuando dos o más ondas se superponen en un punto del espacio, la perturbación resultante en ese punto es la suma algebraica de las perturbaciones individuales causadas por cada una de las ondas. Esto puede resultar en fenómenos como la interferencia constructiva, donde las ondas se refuerzan mutuamente, o la interferencia destructiva, donde las ondas se cancelan entre sí.
En estos ejercicios interactivos, exploraremos diferentes escenarios que implican la superposición de ondas. Desde analizar patrones de interferencia hasta calcular la amplitud y la fase resultantes en puntos específicos, estos ejercicios te ayudarán a comprender mejor cómo aplicar el principio de superposición en situaciones prácticas.
Cuando dos o más ondas existen simultáneamente en el mismo medio, el desplazamiento resultante en cualquier punto y en cualquier instante es...
Selecciona una respuesta.
1 Se sigue del principio de superposición
Cuando la superposición da por resultado una onda
de mayor amplitud, se tiene una interferencia...
Selecciona una respuesta.
1Una interferencia constructiva se tiene cuando la amplitud de una superposición de ondas es mayor que la de cada onda por separado.
Cuando la superposición da por resultado una onda
de menor amplitud, se tiene una interferencia...
Selecciona una respuesta.
1Una interferencia destructiva se tiene cuando la amplitud de una superposición de ondas es menor que la de cada onda por separado.
Dos ondas están descritas por 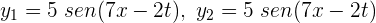 . La superposición de las dos ondas es...
. La superposición de las dos ondas es...
Selecciona una respuesta.
1Por el principio de superposición, el desplazamiento resultante en cualquier punto y en cualquier instante es la suma algebraica de los desplazamientos de cada onda
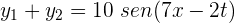
Dos ondas están descritas por 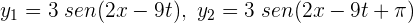 . La superposición de las dos ondas es...
. La superposición de las dos ondas es...
Selecciona una respuesta.
1 Ambas ondas tienen el mismo sentido, magnitud y frecuencia, pero la segunda esta desfazada 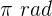 respecto a la primera, luego
respecto a la primera, luego
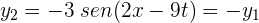
2 Por el principio de superposición, el desplazamiento resultante en cualquier punto y en cualquier instante es la suma algebraica de los desplazamientos de cada onda
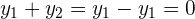
Dos ondas están descritas por 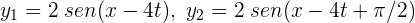 . La superposición de las dos ondas es...
. La superposición de las dos ondas es...
Selecciona una respuesta.
1 Por el principio de superposición, el desplazamiento resultante en cualquier punto y en cualquier instante es la suma algebraica de los desplazamientos de cada onda
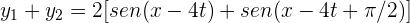
2 Utilizamos la identidad trigonométrica
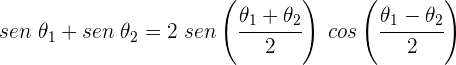
3 Así, el desplazamiento resultante es
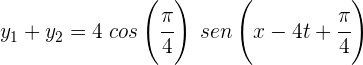
La amplitud de la superposición de las ondas 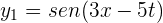 y
y 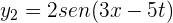 es...
es...
Selecciona una respuesta.
1 Por el principio de superposición, el desplazamiento resultante en cualquier punto y en cualquier instante es la suma algebraica de los desplazamientos de cada onda
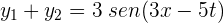
2 La amplitud es 3
La amplitud de la superposición de las ondas 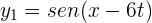 y
y 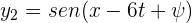 es...
es...
Selecciona una respuesta.
1 Por el principio de superposición, el desplazamiento resultante en cualquier punto y en cualquier instante es la suma algebraica de los desplazamientos de cada onda
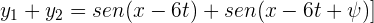
2 Utilizamos la identidad trigonométrica
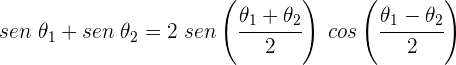
3 Así, el desplazamiento resultante es
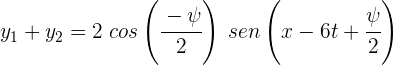
4 Como el coseno es una función par, se tiene
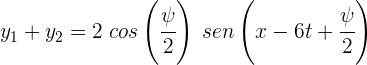
5 Así, la amplitud es 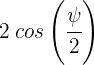
Si 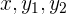 están dados en metros y
están dados en metros y  en segundos, la frecuencia de la onda resultante de la superposición de las ondas
en segundos, la frecuencia de la onda resultante de la superposición de las ondas 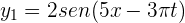 y
y 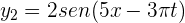 es...
es...
Selecciona una respuesta.
1 Por el principio de superposición, el desplazamiento resultante en cualquier punto y en cualquier instante es la suma algebraica de los desplazamientos de cada onda
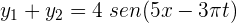
2 Utilizamos la fórmula de la frecuencia
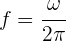
3 Sustituimos los valores conocidos y resolvemos
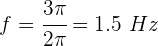
Si 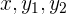 están dados en metros y
están dados en metros y  en segundos, la frecuencia de la onda resultante de la superposición de las ondas
en segundos, la frecuencia de la onda resultante de la superposición de las ondas 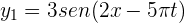 y
y 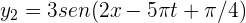 es...
es...
Selecciona una respuesta.
1 Por el principio de superposición, el desplazamiento resultante en cualquier punto y en cualquier instante es la suma algebraica de los desplazamientos de cada onda
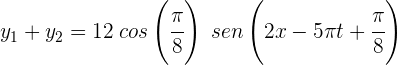
2 Utilizamos la fórmula de la frecuencia
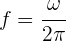
3 Sustituimos los valores conocidos y resolvemos
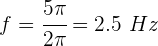
Resumir con IA:


Hola, muchas gracias por compartir estos ejercicios. Me parece que en el ejercicio 3 la respuesta es 2.5Hz y no 0.25Hz. Saludos
La respuesta correcta es 2,5 HZ
Hola te agradecemos tu observación, una disculpa y ya se corrigió.
Holiii. Super buenos ejercicios, pero la tres está mal, pues 1÷0.4s es 2.5hz, no 0.25
Hola te agradecemos tus observaciones y una disculpa, ya se corrigió.
Corrígeme si me equivoco, pero en el 8 el recorrido sería la mitad (600m) , puesto que tarda 1s en llegar al fondo del lago y otro segundo en volver y ser recibida. Un saludo
Hola, me encantaría poder resolver tu dudad, pero necesito que me digas de que tema es tu ejercicio, pues a mi me señala que es un ejercicio de ondas aplicado a un tren de carga y tu mencionas un lago, lo cual me crea dificultades.
La nota musical tiene una frecuencia de 440Hz y tiene una velocidad de 340 m/s en el aire . Calcula su longitud
la 1 esta mal
Hola, disculpa pero podrías señalar porque esta mal, pues no encontré el error.