En los siguientes ejercicios resueltos, exploraremos cómo aplicar las fórmulas de ondas mecánicas y electromagnéticas.
En una alberca se producen ondas estacionarias de 125 cm con una frecuencia de 0.27 Hz. Encuentra la rapidez de las ondas.
1Escribimos los elementos conocidos
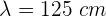
2Convertimos la longitud de onda a metros
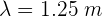
3Empleamos la fórmula de rapidez de onda
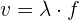
4 Sustituimos los datos conocidos en la fórmula anterior
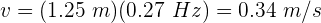
Si el Museo de Guggenheim se mueve con una frecuencia aproximada de 0.06 Hz, encuentra el periodo de la vibración.
1Escribimos los elementos conocidos
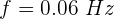
2Sabemos que Hz=1/s, por lo que
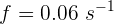
3Empleamos la fórmula de frecuencia de onda
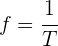
4 Sustituimos los datos conocidos en la fórmula anterior y depejando el periodo se obtiene
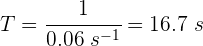
Una cuerda de 10 m se encuentra atada a una pared por uno de sus extremos. Por el otro extremo, la cuerda se mueve de arriba hacia abajo de manera que su periodo es 0.4 s. Encuentra la frecuencia de la vibración.
1Escribimos los elementos conocidos
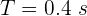
2Empleamos la fórmula de frecuencia de onda
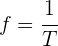
3 Sustituimos los datos conocidos en la fórmula anterior
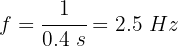
Una onda sonora posee una longitud de 1.5 m y una rapidez de 350 m/s durante 0.8 s. Encuentra la frecuencia de onda y la cantidad de vibraciones que realiza en 0.8 s.
1Escribimos los elementos conocidos
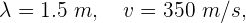
2Empleamos la fórmula de rapidez de onda
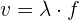
3 Sustituimos los datos conocidos en la fórmula anterior
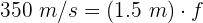
4 Despejando la frecuencia se obtiene
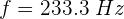
5 La frecuencia nos dice que la onda hace 233.3 vibraciones por segundo, entonces para conocer el número de vibraciones en 0.8 s, realizamos
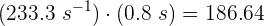
Una onda sonora posee una longitud de 0.9 m y una rapidez de 400 m/s durante 0.8 s. Encuentra el periodo y la distancia a la que se encuentra el frente de la onda sonora a los 0.8 s.
1Escribimos los elementos conocidos
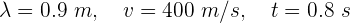
2Empleamos la fórmula de rapidez de onda
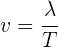
3 Sustituimos los datos conocidos en la fórmula anterior
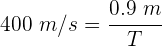
4 Despejando el periodo se obtiene
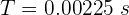
5 Para encontrar la distancia, empleamos la fórmula de rapidez
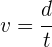
6 Sustituyendo los valores conocidos y despejando la distancia se obtiene
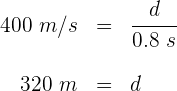
En el agua, el sonido viaja a 1500 m/s. Si un delfin produce un sonido con frecuencia de onda de 2.5 Hz, encuentra su longitud de onda.
1Escribimos los elementos conocidos
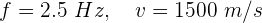
2Empleamos la fórmula de rapidez de onda
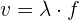
3 Sustituimos los datos conocidos en la fórmula anterior
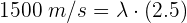
4 Despejando la longitud de onda se obtiene
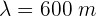
Una fuente genera una onda de longitud 4 m que se propaga en una medio con una rapidez de 3 m/s. Si la fuente aumenta su frecuencia en 0.2 Hz, encuentra el valor de su longitud de onda.
1Escribimos los elementos conocidos
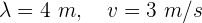
2Empleamos la fórmula de rapidez de onda
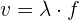
3 Sustituimos los datos conocidos en la fórmula anterior
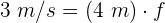
4 Despejando la frecuencia de onda se obtiene
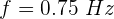
5 Aumentamos la frecuencia en 0.2 Hz, se tiene que la nueva frecuencia es 0.95 Hz. Como la rapidez no cambia en el medio, sustituimos los datos en la fórmula de rapidez de onda
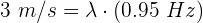
6 Despejando la longitud de onda se obtiene
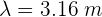
Para conocer la profundidad de un lago se emite una onda con frecuencia de 30 Hz y longitud de onda de 20 m. Si la señal es captada 2 s después de ser emitida, encuentra la profundidad del lago.
1Escribimos los elementos conocidos
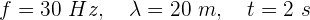
2Empleamos la fórmula de rapidez de onda
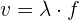
3 Sustituimos los datos conocidos en la fórmula anterior
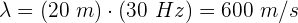
4 Para encontrar la distancia, empleamos la fórmula de rapidez
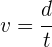
5 Sustituyendo los valores conocidos y despejando la distancia se obtiene
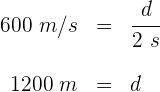
Encuentra la longitud de onda de luz en el vacío que tiene una frecuencia de 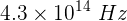 .
.
1Escribimos los elementos conocidos, notando que se trata de una onda electromagnética, por lo que la rapidez es la de la luz
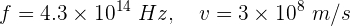
2Empleamos la fórmula de rapidez de onda
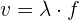
3 Sustituimos los datos conocidos en la fórmula anterior
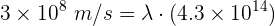
4 Despejando la longitud de onda se obtiene
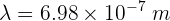
Una onda electromagnética de frecuencia 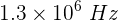 atraviesa un medio de índice de refracción de 1.6. Encuentra la longitud de onda en el medio.
atraviesa un medio de índice de refracción de 1.6. Encuentra la longitud de onda en el medio.
1Escribimos los elementos conocidos, notando que se trata de una onda electromagnética, por lo que la rapidez en el aire es la de la luz
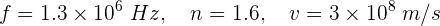
2Empleamos la fórmula de rapidez en el medio
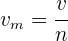
3 Sustituimos los datos conocidos en la fórmula anterior
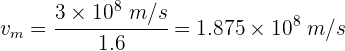
4Empleamos la fórmula de rapidez de onda
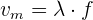
5 Sustituimos los datos conocidos en la fórmula anterior
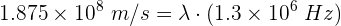
\ Hz
6 Despejando la longitud de onda se obtiene
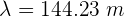
Resumir con IA:



Hola, muchas gracias por compartir estos ejercicios. Me parece que en el ejercicio 3 la respuesta es 2.5Hz y no 0.25Hz. Saludos
La respuesta correcta es 2,5 HZ
Hola te agradecemos tu observación, una disculpa y ya se corrigió.
Holiii. Super buenos ejercicios, pero la tres está mal, pues 1÷0.4s es 2.5hz, no 0.25
Hola te agradecemos tus observaciones y una disculpa, ya se corrigió.
Corrígeme si me equivoco, pero en el 8 el recorrido sería la mitad (600m) , puesto que tarda 1s en llegar al fondo del lago y otro segundo en volver y ser recibida. Un saludo
Hola, me encantaría poder resolver tu dudad, pero necesito que me digas de que tema es tu ejercicio, pues a mi me señala que es un ejercicio de ondas aplicado a un tren de carga y tu mencionas un lago, lo cual me crea dificultades.
La nota musical tiene una frecuencia de 440Hz y tiene una velocidad de 340 m/s en el aire . Calcula su longitud
la 1 esta mal
Hola, disculpa pero podrías señalar porque esta mal, pues no encontré el error.