Sean bienvenidos a esta entra dedicada a presentar ejercicios resueltos de ondas estacionarias, con un enfoque a la resonancia y armónicas. Reforzaremos conceptos fundamentales en la física de las ondas, específicamente en el contexto de cuerdas vibrantes y tubos resonantes, tanto abiertos como cerrados. Estos problemas abordan temas como la frecuencia fundamental, las longitudes de onda de las armónicas, la relación entre la longitud y la frecuencia en sistemas vibrantes, y la velocidad de propagación de las ondas en medios específicos.
Cada ejercicio plantea una situación diferente que requiere la aplicación de fórmulas y conceptos clave de la teoría de ondas para su resolución.
Una cuerda de longitud L tiene una frecuencia fundamental de vibración de 440 Hz. ¿Cuál es la longitud de onda y velocidad de fase de la onda estacionaria correspondiente?
La longitud de onda de la onda estacionaria es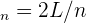 
, donde 
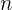es el número de la armónica, mientras que la frecuencia es igual a 
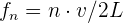, donde 
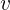es la velocidad de la fase. Como hablamos de frecuencia fundamental, hablamos del caso específico de 
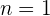. Entonces, la longitud de onda es 
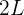, mientras que la velocidad de onda es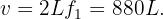 
Un tubo cerrado de longitud L tiene una frecuencia fundamental de vibración de 220 Hz. ¿Cuál es la longitud de onda de la onda estacionaria en el tubo?
En este caso, como tenemos un tubo cerrado, la longitud de onda es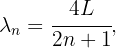
por lo que obtenemos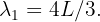
Una cuerda de longitud L tiene una frecuencia fundamental de vibración de 220 Hz. Si se aumenta la tensión en la cuerda al doble, ¿cuál será la nueva frecuencia fundamental?
Al doblar la tension, doblamos la frecuencia. Es decir, la nueva frecuencia fundamental es de 440 Hz.
Un tubo abierto de longitud L tiene una frecuencia fundamental de vibración de 330 Hz. Si se corta el tubo a la mitad (cambiando su longitud a L/2), ¿cuál será la nueva frecuencia fundamental?
La frecuencia se calcula mediante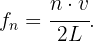 
por lo que obtenemos, al cortar el tubo a la mitad,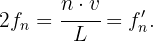
Es decir, doblamos la frecuencia original.
Una cuerda vibra en su segunda armónica con una frecuencia de 880 Hz. Si la longitud de la cuerda es de 0,5 m, ¿cuál es la velocidad de propagación de las ondas en la cuerda?
La velocidad de propagación de las ondas en la cuerda se calcula con la fórmula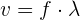 
, donde 
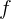es la frecuencia y 
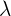es la longitud de onda. En este caso, 
.
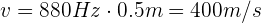Un tubo cerrado tiene una longitud L y vibra en su tercer armónico con una frecuencia de 660 Hz. ¿Cuál es la longitud de onda de la onda estacionaria en el tubo?
La longitud de onda de la onda estacionaria en un tubo cerrado es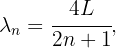
En este caso, tenemos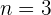 
,
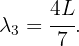
Una cuerda de longitud L tiene una frecuencia fundamental de 440 Hz. Si se corta la cuerda a la mitad (cambiando su longitud a L/2), ¿cuál será la nueva frecuencia fundamental?
Como lo vimos en el caso del tubo abierto, en este caso la frecuencia fundamental se dobla. Es decir, 880Hz.
Un tubo abierto de longitud L tiene una frecuencia fundamental de vibración de 440 Hz. Si se corta el tubo a la mitad (cambiando su longitud a L/2), ¿cuál será la nueva frecuencia fundamental?
Debido a que la fórmula para la frecuencia es igual tanto en cuerdas como en tubos abiertos, obenemos 880Hz.
Un tubo cerrado de longitud L tiene una frecuencia fundamental de vibración de 770 Hz. Si se reduce la longitud del tubo a un tercio (cambiando su longitud a L/3), ¿cuál será la nueva frecuencia fundamental?
La frecuencia se calcula mediante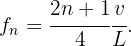 
Entonces, la nueva frecuencia es
Es decir, triplicamos la frecuencia: 2130Hz.
Un tubo cerrado de longitud L tiene una frecuencia fundamental de vibración de 660 Hz. Si se reduce la longitud del tubo a la mitad (cambiando su longitud a L/2), ¿cuál será la nueva frecuencia fundamental?
Igual que al problema anterior, obtenemos el doble de la frecuencia fundamental, es deicr, 1320Hz.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Hola, muchas gracias por compartir estos ejercicios. Me parece que en el ejercicio 3 la respuesta es 2.5Hz y no 0.25Hz. Saludos
Hola te agradecemos tu observación, una disculpa y ya se corrigió.
Holiii. Super buenos ejercicios, pero la tres está mal, pues 1÷0.4s es 2.5hz, no 0.25
Hola te agradecemos tus observaciones y una disculpa, ya se corrigió.
Corrígeme si me equivoco, pero en el 8 el recorrido sería la mitad (600m) , puesto que tarda 1s en llegar al fondo del lago y otro segundo en volver y ser recibida. Un saludo
Hola, me encantaría poder resolver tu dudad, pero necesito que me digas de que tema es tu ejercicio, pues a mi me señala que es un ejercicio de ondas aplicado a un tren de carga y tu mencionas un lago, lo cual me crea dificultades.
La nota musical tiene una frecuencia de 440Hz y tiene una velocidad de 340 m/s en el aire . Calcula su longitud
la 1 esta mal
Hola, disculpa pero podrías señalar porque esta mal, pues no encontré el error.