¡Bienvenidos a la sección de Ejercicios de Inecuaciones de Primer Grado!
Las inecuaciones de primer grado son expresiones algebraicas que involucran variables de primer orden y expresan relaciones de desigualdad. Estas desigualdades son esenciales para modelar situaciones del mundo real donde las cantidades pueden variar de manera continua. En esta serie de ejercicios, exploraremos el fascinante mundo de las inecuaciones y su aplicación en la resolución de problemas prácticos.
A lo largo de estos ejercicios, abordaremos conceptos clave como la representación gráfica de inecuaciones en la recta numérica, la resolución de inecuaciones simples y compuestas, y la interpretación de las soluciones en el contexto de problemas del día a día. Estos problemas te ayudarán a desarrollar habilidades fundamentales para entender y trabajar con inecuaciones, una herramienta poderosa en álgebra y en la modelación de situaciones variadas.

Inecuaciones de una variable
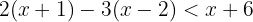
Quitamos paréntesis multiplicando el primero por  y el segundo por
y el segundo por  :
:
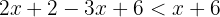
Agrupamos términos semejantes
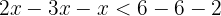
Dividimos por  y cambiamos el sentido de la desigualdad
y cambiamos el sentido de la desigualdad

![]()
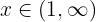
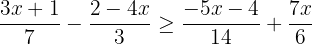
Hallamos el mínimo común múltiplo de los denominadores para quitar denominadores

 se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente
se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente
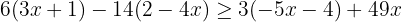
Quitamos paréntesis multiplicando el primero por  , el segundo por
, el segundo por 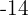 y el tercero por
y el tercero por  :
:

Agrupamos los términos semejantes.
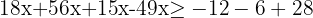
Reducimos los términos semejantes.
Simplificamos dividiendo por 
Dividimos en los dos miembros por 
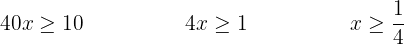
![]()
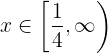
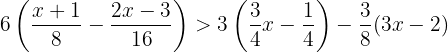
Quitamos paréntesis multiplicando el primero por  y el segundo por
y el segundo por  y el tercero por
y el tercero por 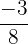 :
:
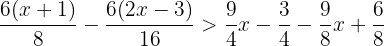
Hallamos el mínimo común múltiplo de los denominadores para quitar denominadores

 se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.
se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.
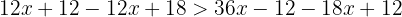
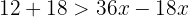
Agrupamos términos, simplificamos dividiendo por  y dividimos en los dos miembros por
y dividimos en los dos miembros por  .
.

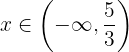
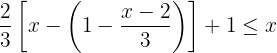
Quitamos el paréntesis multiplicando por  , de modo que el corchete pasa a ser un paréntesis.
, de modo que el corchete pasa a ser un paréntesis.
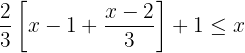
Quitamos paréntesis multiplicando por 
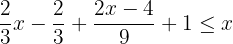
Hallamos el mínimo común múltiplo para quitar denominadores.
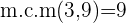
 se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.
se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.

Agrupamos los términos semejantes y realizamos las sumas y restas indicadas
Como el coeficiente de la  es negativo multiplicamos por
es negativo multiplicamos por  , por lo que cambiará el sentido de la desigualdad
, por lo que cambiará el sentido de la desigualdad

![]()
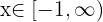
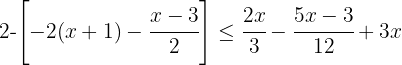
1º Quitar corchetes.
Quitamos el paréntesis multiplicando por  , de modo que el corchete pasa a ser un paréntesis:
, de modo que el corchete pasa a ser un paréntesis:
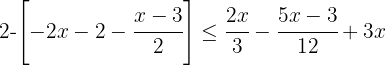
2º Quitar paréntesis.
Quitamos paréntesis multiplicando por  :
:

3º Quitar denominadores.
Hallamos el mínimo común múltiplo:
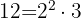
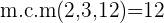
 se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.
se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.
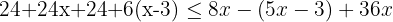
Quitamos paréntesis multiplicando el primero por  y el segundo por
y el segundo por  :
:

4º Agrupamos los términos en  a un lado de la desigualdad y los términos independientes en el otro.
a un lado de la desigualdad y los términos independientes en el otro.

5º Efectuamos las operaciones
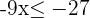
6º Si el coeficiente de la  es negativo multiplicamos por
es negativo multiplicamos por  , por lo que cambiará el sentido de la desigualdad.
, por lo que cambiará el sentido de la desigualdad.
Este paso los haremos siempre antes de despejar la incógnita

7º Despejamos la incógnita, dividiendo en los dos miembros por  .
.

En la práctica se suele decir que el  está multiplicando y pasa al otro miembro dividiendo a
está multiplicando y pasa al otro miembro dividiendo a  .
.

Obtenemos la solución como una desigualdad, pero ésta también podemos expresarla:
De forma gráfica

Como un intervalo
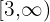
Calcula el valor que se indica
Halla los valores de  para los que las raíces de la ecuación
para los que las raíces de la ecuación 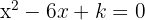 sean las dos reales y distintas.
sean las dos reales y distintas.
Para que la ecuación tenga dos raíces reales y distintas el discriminante 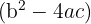 tiene que ser mayor que cero.
tiene que ser mayor que cero.
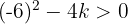
Resolvemos la inecuación:
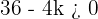
Multiplicamos por  y cambiamos el signo de la desigualdad.
y cambiamos el signo de la desigualdad.


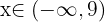
Halla los valores de  para los que las raíces de la ecuación
para los que las raíces de la ecuación 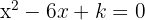 sean las dos reales e iguales.
sean las dos reales e iguales.
Para que la ecuación tenga dos raíces reales e iguales el discriminante 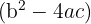 tiene que ser igual que cero.
tiene que ser igual que cero.
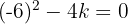
Resolvemos la ecuación:
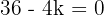
Multiplicamos por  y cambiamos el signo de la igualdad.
y cambiamos el signo de la igualdad.

Halla los valores de  para los que las raíces de la ecuación
para los que las raíces de la ecuación 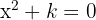 sean las dos reales y distintas.
sean las dos reales y distintas.
Para que la ecuación tenga dos raíces reales y distintas el discriminante 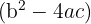 tiene que ser mayor que cero.
tiene que ser mayor que cero.
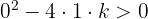
Resolvemos la inecuación:
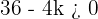
Multiplicamos por  y cambiamos el signo de la desigualdad.
y cambiamos el signo de la desigualdad.

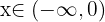
Halla los valores de  para los que las raíces de la ecuación
para los que las raíces de la ecuación 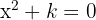 sean imaginarias.
sean imaginarias.
Para que la ecuación tenga dos raíces imaginarias el discriminante 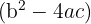 tiene que ser menor que cero.
tiene que ser menor que cero.
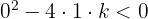
Resolvemos la inecuación:
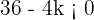
Multiplicamos por  y cambiamos el signo de la desigualdad.
y cambiamos el signo de la desigualdad.

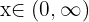
Halla los valores de  para los que las raíces de la ecuación
para los que las raíces de la ecuación 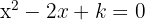 sean imaginarias.
sean imaginarias.
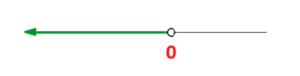
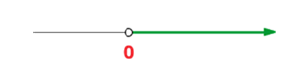
Necesitamos que el discriminante satisfaga
Es decir, toda la recta 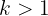 hace que la ecuación no tenga raíces reales.
hace que la ecuación no tenga raíces reales.
Inecuaciones de dos variables


1º Transformamos la desigualdad en igualdad.

2º Damos a la variable x dos valores, con lo que obtenemos dos puntos.




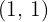
3º Al representar y unir estos puntos obtenemos una recta.

Tomamos el punto  y lo sustituimos en la inecuación.
y lo sustituimos en la inecuación.

Como se cumple la desigualdad la solución es el semi-plano donde se encuentra  , incluyendo la recta porque tomamos los puntos menores y también los iguales.
, incluyendo la recta porque tomamos los puntos menores y también los iguales.
En este caso dibujamos la recta con trazo continuo.

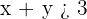
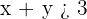
1º Transformamos la desigualdad en igualdad.
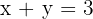
2º Damos a la variable x dos valores, con lo que obtenemos dos puntos.


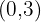


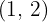
Tomamos el punto  y lo sustituimos en la inecuación.
y lo sustituimos en la inecuación.

Como no se cumple la desigualdad la solución es el semi-plano donde no se encuentra  , sin incluir la recta porque tomamos los puntos menores.
, sin incluir la recta porque tomamos los puntos menores.
En este caso dibujamos la recta con trazo continuo.
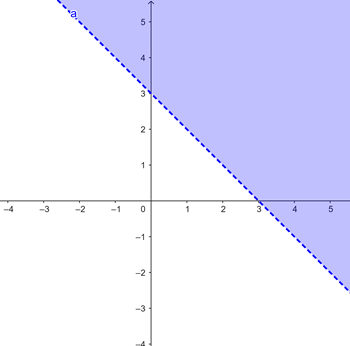
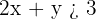
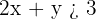
1º Transformamos la desigualdad en igualdad.

2º Damos a la variable  dos valores, con lo que obtenemos dos puntos.
dos valores, con lo que obtenemos dos puntos.


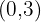


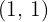
3º Al representar y unir estos puntos obtenemos una recta.

Tomamos el punto  y lo sustituimos en la inecuación.
y lo sustituimos en la inecuación.

Como no se cumple la desigualdad, la solución es el semi-plano donde no se encuentra 
En este caso (mayor que, pero no igual) los puntos de la recta no pertenecen a la solución.
En este caso dibujamos la recta con trazo discontinuo

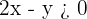
1º Transformamos la desigualdad en igualdad.
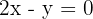
2º Damos a la variable  dos valores, con lo que obtenemos dos puntos.
dos valores, con lo que obtenemos dos puntos.





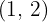
Tomamos el punto  y lo sustituimos en la inecuación.
y lo sustituimos en la inecuación.
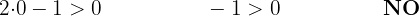
Como no se cumple la desigualdad, la solución es el semi-plano donde no se encuentra 
En este caso (mayor que, pero no igual) los puntos de la recta no pertenecen a la solución.
En este caso dibujamos la recta con trazo discontinuo
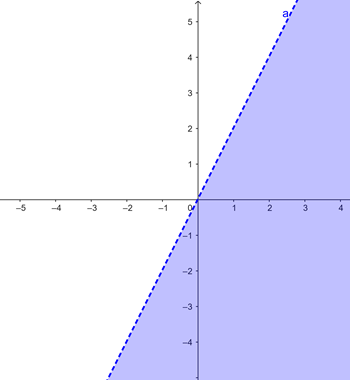
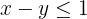
Despejando para  , tenemos la desigualdad
, tenemos la desigualdad  . Recordemos que la recta
. Recordemos que la recta 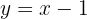 tiene pendiente 1 y pasa por los puntos
tiene pendiente 1 y pasa por los puntos 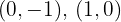 , por lo que la desigualdad nos proporciona la parte superior de esta región:
, por lo que la desigualdad nos proporciona la parte superior de esta región: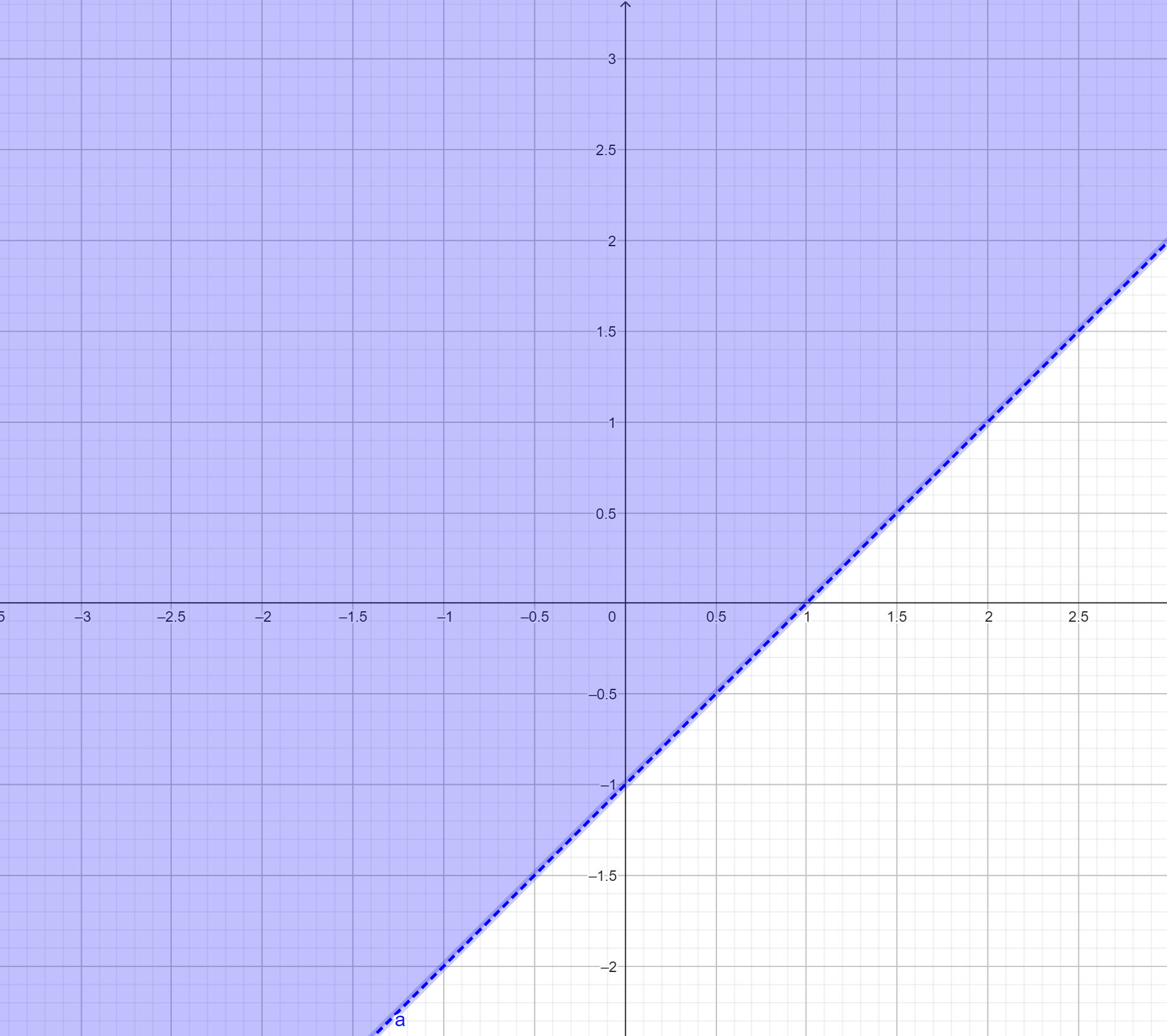
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Ayúdame a resolver esto: una hamburguesa cuesta $5 y un gaseosa $2. Un cliente tiene máximo $20.¿Cuántas hamburguesas y gaseosas puede comprar?
✅ Datos
Precio de una hamburguesa = $5
Precio de una gaseosa = $2
Dinero máximo = $20
Buscamos todas las combinaciones posibles con:
5
ℎ
+
2
𝑔
≤
20
5h+2g≤20
donde h = hamburguesas (entero ≥ 0)
y g = gaseosas (entero ≥ 0)
✅ Probando cada cantidad de hamburguesas
Si compra 0 hamburguesas
Usa solo gaseosas:
$20 ÷ $2 = 10 gaseosas
➡ (0 hamburguesas, 10 gaseosas)
Si compra 1 hamburguesa
Costo hamburguesas: 1 × 5 = $5
Dinero restante: 20 – 5 = $15
Gaseosas: 15 ÷ 2 = 7.5 → solo se puede 7 gaseosas
➡ (1 hamburguesa, 7 gaseosas)
Si compra 2 hamburguesas
Costo: 2 × 5 = $10
Resto: 20 – 10 = $10
Gaseosas: 10 ÷ 2 = 5 gaseosas
➡ (2 hamburguesas, 5 gaseosas)
Si compra 3 hamburguesas
Costo: 3 × 5 = $15
Resto: 20 – 15 = $5
Gaseosas: 5 ÷ 2 = 2.5 → solo 2 gaseosas
➡ (3 hamburguesas, 2 gaseosas)
Si compra 4 hamburguesas
Costo: 4 × 5 = $20
Resto: 0
Gaseosas: 0
➡ (4 hamburguesas, 0 gaseosas)
Si compra 5 hamburguesas
5 × 5 = $25, eso pasa de $20 ❌ No se puede
✅ Todas las combinaciones válidas
Hamburguesas Gaseosas Total
0 10 0×5 + 10×2 = 20
1 7 1×5 + 7×2 = 19
2 5 2×5 + 5×2 = 20
3 2 3×5 + 2×2 = 19
4 0 4×5 + 0 = 20
✅ Estas son todas las combinaciones posibles con máximo $20.
3 hamburguesas y 2 gaseosas
En el ejercicio 9 de inecuaciones hay un error en el resultado, crec. Pone (-4,3) U (3,4) y creo que deberia ser (-4,-3)U(3,4). S no no lo comprendo.
Hola, fue un error nuestro discúlpanos ya se corrigió y gracias por tu ayuda.
48x+12>108
10(×+1)+<6(2×+1)