Una desigualdad fraccionaria es una desigualdad en la que la incognita está tanto en el denominador como en el numerador. En general las desigualdades fraccionarias tienen alguna de las siguientes formas
1 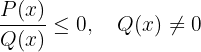
2 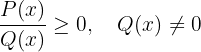
3 
4 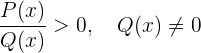
Nos enfocaremos en explicar los primeros dos casos sobre como proceder. Los pasos son sencillos, lo que debemos es encontrar los valores de  en el numerador y el denominador para los cuales se cumple la desigualdad, normalmente terminamos tomandao intersecciones y uniones de los intervalos.
en el numerador y el denominador para los cuales se cumple la desigualdad, normalmente terminamos tomandao intersecciones y uniones de los intervalos.
Primer caso importante
Empezaremos con 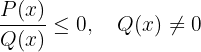 .
.
1 Primero debemos encontrar los valores para los cuales 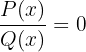 , esto lo hacemos encontrar los valores de
, esto lo hacemos encontrar los valores de  para los cuales el numerador es igual a cero, esto es, resolvemos
para los cuales el numerador es igual a cero, esto es, resolvemos 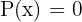 . Denotaremos el conjunto de valores para los cuales
. Denotaremos el conjunto de valores para los cuales 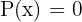 como
como  .
.
2 Tenemos que 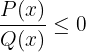 , como ya encontramos los valores cuando es igual a cero, ahora solo nos enfocaremos en
, como ya encontramos los valores cuando es igual a cero, ahora solo nos enfocaremos en 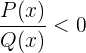 .
.
Tenemos dos casos en los cuales 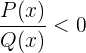 , recordemos que esto sucede siempre que el denominador
, recordemos que esto sucede siempre que el denominador  y
y  tengan signos opuestos.Así, nuestro primer caso es
tengan signos opuestos.Así, nuestro primer caso es  y
y 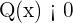 . Digamos que el conjunto de valores para los cuales
. Digamos que el conjunto de valores para los cuales  es
es  , y el conjunto de valores para los cuales
, y el conjunto de valores para los cuales 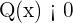 como
como  , entonces, el conjunto de solución para el cual se cumplen ambas desigualdes
, entonces, el conjunto de solución para el cual se cumplen ambas desigualdes  y
y 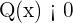 es la intersección
es la intersección  . Ojo, notemos que tomamos
. Ojo, notemos que tomamos 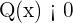 y no
y no  ya que
ya que  es el denominador y no puede ser igual a cero.
es el denominador y no puede ser igual a cero.
Nuestro segundo caso es 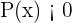 y
y 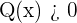 . Digamos que el conjunto de valores para los cuales
. Digamos que el conjunto de valores para los cuales 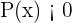 es
es  , y el conjunto de valores para los cuales
, y el conjunto de valores para los cuales 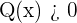 como
como  , entonces, el conjunto de solución para el cual se cumplen ambas desigualdes
, entonces, el conjunto de solución para el cual se cumplen ambas desigualdes 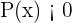 y
y 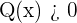 es la intersección
es la intersección  . Ojo, notemos que tomamos
. Ojo, notemos que tomamos 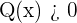 y no
y no 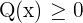 ya que
ya que  es el denominador y no puede ser igual a cero.
es el denominador y no puede ser igual a cero.
3 El conjunto solución es la unión de los conjuntos  ,
, 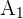 y
y 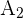 , esto es
, esto es

Para el caso  es similar, pero solo nos enfocamos en el segundo y tercer punto.
es similar, pero solo nos enfocamos en el segundo y tercer punto.
Segundo caso importante
Ahora analicemos el caso cuando 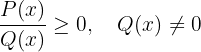
1 Primero debemos encontrar los valores para los cuales 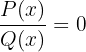 , esto lo hacemos encontrar los valores de
, esto lo hacemos encontrar los valores de  paara los cuales el numerador es igual a cero, esto es, resolvemos
paara los cuales el numerador es igual a cero, esto es, resolvemos 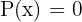 . Denotaremos el conjunto de valores para los cuales
. Denotaremos el conjunto de valores para los cuales 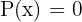 como
como  .
.
2 Tenemos que 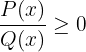 , como ya encontramos los valores cuando es igual a cero, ahora solo nos enfocaremos en
, como ya encontramos los valores cuando es igual a cero, ahora solo nos enfocaremos en 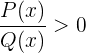 .
.
Tenemos dos casos en los cuales 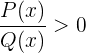 , recordemos que esto sucede siempre que el denominador
, recordemos que esto sucede siempre que el denominador  y
y  tengan signos iguales. Así, nuestro primer caso es
tengan signos iguales. Así, nuestro primer caso es  y
y 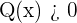 . Digamos que el conjunto de valores para los cuales
. Digamos que el conjunto de valores para los cuales  es
es  , y el conjunto de valores para los cuales
, y el conjunto de valores para los cuales 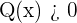 como
como  , entonces, el conjunto de solución para el cual se cumplen ambas desigualdes
, entonces, el conjunto de solución para el cual se cumplen ambas desigualdes  y
y 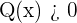 es la intersección
es la intersección  . Ojo, notemos que tomamos
. Ojo, notemos que tomamos 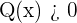 y no
y no 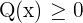 ya que
ya que  es el denominador y no puede ser igual a cero.
es el denominador y no puede ser igual a cero.
Nuestro segundo caso es 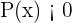 y
y 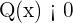 . Digamos que el conjunto de valores para los cuales
. Digamos que el conjunto de valores para los cuales 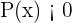 es
es  , y el conjunto de valores para los cuales
, y el conjunto de valores para los cuales 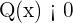 como
como  , entonces, el conjunto de solución para el cual se cumplen ambas desigualdes
, entonces, el conjunto de solución para el cual se cumplen ambas desigualdes 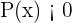 y
y 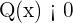 es la intersección
es la intersección  . Ojo, notemos que tomamos
. Ojo, notemos que tomamos 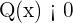 y no
y no  ya que
ya que  es el denominador y no puede ser igual a cero.
es el denominador y no puede ser igual a cero.
3 El conjunto solución es la unión de los conjuntos  ,
, 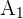 y
y 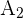 , esto es
, esto es

Para el caso 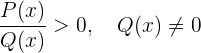 es similar, pero solo nos enfocamos en el segundo y tercer punto.
es similar, pero solo nos enfocamos en el segundo y tercer punto.
Ejemplos
Normalmente es esto ejercicios  y
y  son monomios o producto de monomios. Analicemos los siguientes ejemplos para entender a fondo el procedimiento:
son monomios o producto de monomios. Analicemos los siguientes ejemplos para entender a fondo el procedimiento:
1 Resuelve la siguiente inecuación

En este caso  y
y 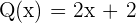 . Empecemos analizando cuando
. Empecemos analizando cuando

Para esto necesitamos encontrar cuándo 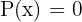 , o bien
, o bien 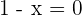 , es claro que esto sucede cuando
, es claro que esto sucede cuando  . Así, nuestro primer conjunto es
. Así, nuestro primer conjunto es 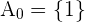 . Ahora procedaos a analizando cuando
. Ahora procedaos a analizando cuando

Ya sabemos que para esto tenemos dos casos, que es cuando el denominador y el numerador tienen signos opuestos. Empecemos por el primer caso
1  y
y 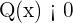 .
.
Ya sabemos que esto es equivalente a  y
y  . De la primer desigualdad tenemos
. De la primer desigualdad tenemos
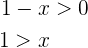
de donde se sigue que el conjunto solución de esta desigualdad es 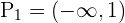 . De la segunda tenemos
. De la segunda tenemos
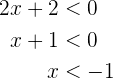
de donde se sigue que el conjunto solución de esta desigualdad es 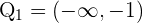 . Así el conjunto solución para este caso es la intersección, la cual es
. Así el conjunto solución para este caso es la intersección, la cual es
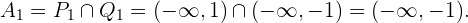
2 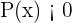 y
y 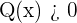 .
.
Ya sabemos que esto es equivalente a 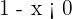 y
y 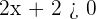 . De la primer desigualdad tenemos
. De la primer desigualdad tenemos
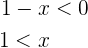
de donde se sigue que el conjunto solución de esta desigualdad es 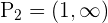 . De la segunda tenemos
. De la segunda tenemos
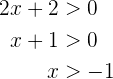
de donde se sigue que el conjunto solución de esta desigualdad es  . Así el conjunto solución para este caso es la intersección, la cual es
. Así el conjunto solución para este caso es la intersección, la cual es
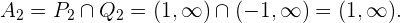
Por últimos, tenemos que la solución general de nuestra inecuación es la unión de nuestras tres soluciones  ,
, 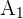 y
y 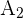 , esto es
, esto es
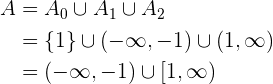
¿Buscas clases particulares de algebra lineal?
2 Resuelve la siguiente inecuación

En este caso 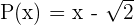 y
y 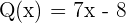 . Notemos que como aquí es estrictamente mayor, no nos importa cuando la fracción es igual a cero, por lo tanto nos brincamos a analizar directamente la desigualdad. Para esto tenemos dos casos, que es cuando tanto numerados como denominador tienen el mismo signo. Empecemos por el primer caso
. Notemos que como aquí es estrictamente mayor, no nos importa cuando la fracción es igual a cero, por lo tanto nos brincamos a analizar directamente la desigualdad. Para esto tenemos dos casos, que es cuando tanto numerados como denominador tienen el mismo signo. Empecemos por el primer caso
1  y
y 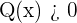 .
.
Ya sabemos que esto es equivalente a  y
y  . De la primer desigualdad tenemos
. De la primer desigualdad tenemos

de donde se sigue que el conjunto solución de esta desigualdad es 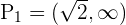 . De la segunda tenemos
. De la segunda tenemos
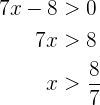
de donde se sigue que el conjunto solución de esta desigualdad es 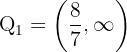 . Así el conjunto solución para este caso es la intersección, la cual es
. Así el conjunto solución para este caso es la intersección, la cual es
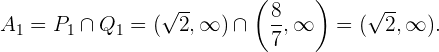
2 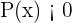 y
y 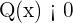 .
.
Ya sabemos que esto es equivalente a 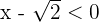 y
y 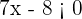 . De la primer desigualdad tenemos
. De la primer desigualdad tenemos
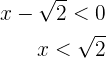
de donde se sigue que el conjunto solución de esta desigualdad es 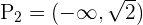 . De la segunda tenemos
. De la segunda tenemos

de donde se sigue que el conjunto solución de esta desigualdad es 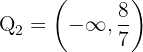 . Así el conjunto solución para este caso es la intersección, la cual es
. Así el conjunto solución para este caso es la intersección, la cual es
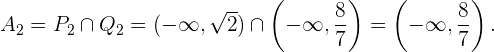
Por últimos, tenemos que la solución general de nuestra inecuación es la unión de nuestras dos soluciones 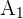 y
y 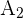 , esto es
, esto es
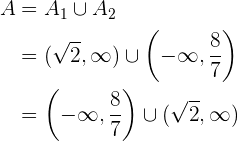
3 Resuelve la siguiente inecuación

En este caso 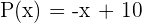 y
y 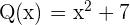 . Empecemos analizando cuando
. Empecemos analizando cuando

Para esto necesitamos encontrar cuándo 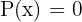 , o bien
, o bien 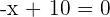 , es claro que esto sucede cuando
, es claro que esto sucede cuando 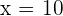 . Así, nuestro primer conjunto es
. Así, nuestro primer conjunto es 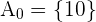 . Ahora procedaos a analizando cuando
. Ahora procedaos a analizando cuando

Ya sabemos que para esto tenemos dos casos, que es cuando el numerador y el denominador tienen signos opuesto. Empecemos por el primer caso
1  y
y 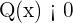 .
.
Notemos que se nos pide que 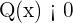 , lo cual es equivalente a
, lo cual es equivalente a
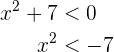
Sin embargo  para todo
para todo 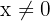 , por lo tanto, lo de arriba nos pide que
, por lo tanto, lo de arriba nos pide que
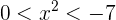
lo cual nos lleva a 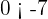 , lo cual no puede pasar nunca. Esto nos dice que no se puede cumplir que
, lo cual no puede pasar nunca. Esto nos dice que no se puede cumplir que 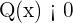 , por lo tanto, en este caso,
, por lo tanto, en este caso,
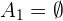
2 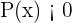 y
y 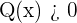 .
.
Ya sabemos que esto es equivalente a 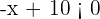 y
y 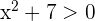 . De la primer desigualdad tenemos
. De la primer desigualdad tenemos
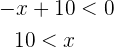
de donde se sigue que el conjunto solución de esta desigualdad es 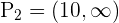 . De la segunda tenemos
. De la segunda tenemos 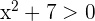 se cumple para todo
se cumple para todo  , por lo tanto se sigue que el conjunto solución de esta desigualdad es
, por lo tanto se sigue que el conjunto solución de esta desigualdad es 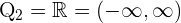 . Así el conjunto solución para este caso es la intersección, la cual es
. Así el conjunto solución para este caso es la intersección, la cual es
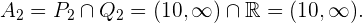
Por últimos, tenemos que la solución general de nuestra inecuación es la unión de nuestras tres soluciones  ,
, 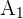 y
y 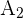 , esto es
, esto es
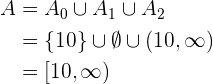
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Ayúdame a resolver esto: una hamburguesa cuesta $5 y un gaseosa $2. Un cliente tiene máximo $20.¿Cuántas hamburguesas y gaseosas puede comprar?
✅ Datos
Precio de una hamburguesa = $5
Precio de una gaseosa = $2
Dinero máximo = $20
Buscamos todas las combinaciones posibles con:
5
ℎ
+
2
𝑔
≤
20
5h+2g≤20
donde h = hamburguesas (entero ≥ 0)
y g = gaseosas (entero ≥ 0)
✅ Probando cada cantidad de hamburguesas
Si compra 0 hamburguesas
Usa solo gaseosas:
$20 ÷ $2 = 10 gaseosas
➡ (0 hamburguesas, 10 gaseosas)
Si compra 1 hamburguesa
Costo hamburguesas: 1 × 5 = $5
Dinero restante: 20 – 5 = $15
Gaseosas: 15 ÷ 2 = 7.5 → solo se puede 7 gaseosas
➡ (1 hamburguesa, 7 gaseosas)
Si compra 2 hamburguesas
Costo: 2 × 5 = $10
Resto: 20 – 10 = $10
Gaseosas: 10 ÷ 2 = 5 gaseosas
➡ (2 hamburguesas, 5 gaseosas)
Si compra 3 hamburguesas
Costo: 3 × 5 = $15
Resto: 20 – 15 = $5
Gaseosas: 5 ÷ 2 = 2.5 → solo 2 gaseosas
➡ (3 hamburguesas, 2 gaseosas)
Si compra 4 hamburguesas
Costo: 4 × 5 = $20
Resto: 0
Gaseosas: 0
➡ (4 hamburguesas, 0 gaseosas)
Si compra 5 hamburguesas
5 × 5 = $25, eso pasa de $20 ❌ No se puede
✅ Todas las combinaciones válidas
Hamburguesas Gaseosas Total
0 10 0×5 + 10×2 = 20
1 7 1×5 + 7×2 = 19
2 5 2×5 + 5×2 = 20
3 2 3×5 + 2×2 = 19
4 0 4×5 + 0 = 20
✅ Estas son todas las combinaciones posibles con máximo $20.
3 hamburguesas y 2 gaseosas
En el ejercicio 9 de inecuaciones hay un error en el resultado, crec. Pone (-4,3) U (3,4) y creo que deberia ser (-4,-3)U(3,4). S no no lo comprendo.
Hola, fue un error nuestro discúlpanos ya se corrigió y gracias por tu ayuda.
48x+12>108
10(×+1)+<6(2×+1)