Las inecuaciones son expresiones matemáticas que establecen una relación de desigualdad entre dos cantidades. A diferencia de las ecuaciones, que buscan igualar dos expresiones, las inecuaciones nos permiten representar un rango de valores que cumplen con ciertas condiciones. Estas se utilizan ampliamente en diversas disciplinas, como la economía, la física y la estadística, para modelar situaciones reales donde las cantidades no son fijas.
En estos ejercicio se supondrá que ya se tiene conocimiento sobre la definición de inecuación y algunas de sus propiedades. En caso de no ser así se sugiere visitar nuestro artículo sobre teoría.
Resolveremos cada uno de los ejercicios paso a paso. Debemos notar que resolver una inecuación es prácticamente igual que hacer un despeje en una igualdad, simplemente que ahora debemos prestar mucha atención sobre las propiedades de inecuaciones, cuándo éstas "cambian de sentido", etc. Haremos cada paso algebraico, intentando ser lo más detallados posibles.
Encuentra la solucion de cada una de las siguienes inecuaciones, o sistemas de inecuaciones y grafica su conjunto solución.
2x + 5 < x - 6
Procedamos a resolver la inecuación, recuerda que es muy parecido a un despeje en una igualdad, solo que ahora en vez de encontrar únicamente un valor para nuestra variable, encontramos todo un dominio, muchas veces formado por un intervalo o por uniones o intercepciones de intervalos. Nuestra inecuación es

Notemos que esto nos dice que  , o bien, tenemos que su conjunto de solución es el intervalo
, o bien, tenemos que su conjunto de solución es el intervalo  .
.

Procedamos, para esto primero haremos uso de la propiedades distributiva y luego despejaremos 

Notemos que esto nos dice que  , o bien, tenemos que su conjunto de solución es el intervalo
, o bien, tenemos que su conjunto de solución es el intervalo  .
.


Procedamos, para esto nos desharemos de las fracciones primero y luego despejaremos  . Para deshacernos de las fracciones necesitamos el mínimo común múltiplo de los denominadores, el cual es
. Para deshacernos de las fracciones necesitamos el mínimo común múltiplo de los denominadores, el cual es  , así, obtenemos
, así, obtenemos

Notemos que esto nos dice que  , o bien, tenemos que su conjunto de solución es el intervalo
, o bien, tenemos que su conjunto de solución es el intervalo  .
.

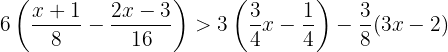
Procedamos, para esto, al igual que en los ejercicio anteriores, necesitamos aplicar ley distributiva y, además, eliminar las fracciones

Notemos que esto nos dice que  , o bien, tenemos que su conjunto de solución es el intervalo
, o bien, tenemos que su conjunto de solución es el intervalo  .
.

Para resolver este sistema debemos resolver las inecuaciones por serparado y luego encontrar los valores para los cuales  cumple ambas inecuaciones.
cumple ambas inecuaciones.
Empecemos con la primer inecuación

así, de la primer inecuación tenemos que  , o bien, que
, o bien, que  pertenece al intervalo
pertenece al intervalo  . Ahora resolvamos la segunda inecuación
. Ahora resolvamos la segunda inecuación

así, de la segunda inecuación tenemos que  , o bien, que
, o bien, que  pertenece al intervalo
pertenece al intervalo  . Notemos que equis debe cumplir ambas condiciones, esto es,
. Notemos que equis debe cumplir ambas condiciones, esto es,  y
y  , esto es equivalente a decir que
, esto es equivalente a decir que  se encuentra en la intersección de los intervalos
se encuentra en la intersección de los intervalos  y
y  , así, el conjunto solución es
, así, el conjunto solución es



Procedamos a resolver el ejercicio

Notemos que esto nos dice que  , sin embargo, el producto es negativo únicamente cuando las expresiones que se multiplican tienen signos contrarios, esto es, tenemos dos casos principales, uno es que
, sin embargo, el producto es negativo únicamente cuando las expresiones que se multiplican tienen signos contrarios, esto es, tenemos dos casos principales, uno es que  y
y  , o bien, el otro caso es que
, o bien, el otro caso es que  y
y  .
.
Evaluemos cada caso, empecemos con el primero que mencionamos. Supongamos que  , entonces
, entonces  , además, tenemos que
, además, tenemos que  , entonces
, entonces  , esto es
, esto es  debe cumplir que
debe cumplir que  y
y  , o bien, debe pertenecer a la intersección de los intervalos
, o bien, debe pertenecer a la intersección de los intervalos  y
y  . Notemos que la intersección es vacía, dichos intervalos no intersectan, por lo tanto, de este caso no obtenemos solución alguna.
. Notemos que la intersección es vacía, dichos intervalos no intersectan, por lo tanto, de este caso no obtenemos solución alguna.
Ahora procedamos con el segundo caso, supongamos que  , entonces
, entonces  , además, tenemos que
, además, tenemos que  , entonces
, entonces  , esto nos dice que
, esto nos dice que  debe cumplir que
debe cumplir que  y
y  , o bien, debe pertenecer a la intersección de los intervalos
, o bien, debe pertenecer a la intersección de los intervalos  y
y  . Notemos que la intersección es
. Notemos que la intersección es  , dicho intervalo es la solución que buscamos.
, dicho intervalo es la solución que buscamos.


Procedamos a resolver el ejercicio

Notemos que para expresar a  como producto de expresiones de primier grado debemos encontrar sus raíces, para esto, utilizando la fórmula cuadrática tenemos que
como producto de expresiones de primier grado debemos encontrar sus raíces, para esto, utilizando la fórmula cuadrática tenemos que

sin embargo, notemos que tenemos la raíz cuadrada de un número negativo, por lo tanto las raíces del polinomio son ambas números complejos. Dicho lo anterior, como no podemos escribir el polinomio como producto de expresiones de primer grado reales, para encontrar solución sustituiremos  por un número real cualquiera que elijamos, si la inecuación se cumple, tendremos que entonces la solución es el conjunto de los números reales
por un número real cualquiera que elijamos, si la inecuación se cumple, tendremos que entonces la solución es el conjunto de los números reales  , en caso de no cumplirse, entonces tendremos que no existe solución. Sustuyamos
, en caso de no cumplirse, entonces tendremos que no existe solución. Sustuyamos  , así
, así

Como es cierto que  , entonces el conjunto solución es
, entonces el conjunto solución es  .
.

Procedamos a resolver

Notemos que al final dividí entre  , esto es porque al ser la expresión estrictamente positiva, es imposible que
, esto es porque al ser la expresión estrictamente positiva, es imposible que  , por lo tanto
, por lo tanto  . Ahora, calculando las raíces de
. Ahora, calculando las raíces de  podemos escribir nuestra inecuación como
podemos escribir nuestra inecuación como

Esto nos dice que  , sin embargo, el producto es positivo únicamente cuando las expresiones que se multiplican tienen el mismo signo, esto es, tenemos dos casos principales, uno es que
, sin embargo, el producto es positivo únicamente cuando las expresiones que se multiplican tienen el mismo signo, esto es, tenemos dos casos principales, uno es que  y
y  , o bien, el otro caso es que
, o bien, el otro caso es que  y
y  .
.
Evaluemos cada caso, empecemos con el primero que mencionamos. Supongamos que  , entonces
, entonces  , además, tenemos que
, además, tenemos que  , entonces
, entonces  , esto es
, esto es  debe cumplir que
debe cumplir que  y
y  , o bien, debe pertenecer a la intersección de los intervalos
, o bien, debe pertenecer a la intersección de los intervalos  y
y  . Notemos que la intersección es
. Notemos que la intersección es  , por lo tanto esta es una solución.
, por lo tanto esta es una solución.
Ahora procedamos con el segundo caso, supongamos que  , entonces
, entonces  , además, tenemos que
, además, tenemos que  , entonces
, entonces  , esto nos dice que
, esto nos dice que  debe cumplir que
debe cumplir que  y
y  , o bien, debe pertenecer a la intersección de los intervalos
, o bien, debe pertenecer a la intersección de los intervalos  y
y  . Notemos que la intersección es
. Notemos que la intersección es  , dicho intervalo también es solución.
, dicho intervalo también es solución.
Así, nuestra solución final es la unión de las dos soluciones individuales que encontramos, esto es, la solución final es  .
.


Procedamos a resolver el ejercicio

Esto nos dice que  , sin embargo, el producto es negativo únicamente cuando las expresiones que se multiplican tienen signos opuestoso, esto es, tenemos dos casos principales, uno es que
, sin embargo, el producto es negativo únicamente cuando las expresiones que se multiplican tienen signos opuestoso, esto es, tenemos dos casos principales, uno es que  y
y  , o bien, el otro caso es que
, o bien, el otro caso es que  y
y  .
.
Evaluemos cada caso, empecemos con el primero que mencionamos. Supongamos que  , primero, de nuevo debemos expresar este este polinomio de segundo orden como producto de expresiones de primer grado, esto es
, primero, de nuevo debemos expresar este este polinomio de segundo orden como producto de expresiones de primer grado, esto es

Para que esto sea positivo se debe cumplir también que  y
y  sean del mismo signo, esto es, que ambos sean positivos o ambos negativos. Suponiendo que ambos son negativos, tenemos que
sean del mismo signo, esto es, que ambos sean positivos o ambos negativos. Suponiendo que ambos son negativos, tenemos que  , entonces,
, entonces,  y
y  , entonces,
, entonces,  , esto es equivalente a decir que
, esto es equivalente a decir que  pertenece a la intersección de los intervalos
pertenece a la intersección de los intervalos  y
y  la cual es
la cual es  .
.
Ahora supongamos que  y
y  son positivos, tenemos que
son positivos, tenemos que  , entonces,
, entonces,  y
y  , entonces,
, entonces,  , esto es equivalente a decir que
, esto es equivalente a decir que  pertenece a la intersección de los intervalos
pertenece a la intersección de los intervalos  y
y  la cual es
la cual es  .
.
Así, para que se cumpla que  se debe tener que
se debe tener que  pertenezca a la unión de los dos intervalos que encontramos previamente, esto es,
pertenezca a la unión de los dos intervalos que encontramos previamente, esto es,  pertenece a
pertenece a  .
.
Como la suposición es que  , también se tiene que
, también se tiene que  , debemos expresar este este polinomio de segundo orden como producto de expresiones de primer grado, esto es
, debemos expresar este este polinomio de segundo orden como producto de expresiones de primer grado, esto es

Para que esto sea negativo se debe cumplir también que  y
y  tengan signos opuestos. Suponiendo que
tengan signos opuestos. Suponiendo que  y
y  tenemos que
tenemos que  y
y  respectivamente, esto es,
respectivamente, esto es,  pertenece a la intersección de los intervalos
pertenece a la intersección de los intervalos  y
y  la cual es
la cual es  .
.
Ahora supongamos que  y
y  tenemos que
tenemos que  y
y  respectivamente, esto es,
respectivamente, esto es,  pertenece a la intersección de los intervalos
pertenece a la intersección de los intervalos  y
y  la cual es vacía. Así, la única forma de que
la cual es vacía. Así, la única forma de que  es que
es que  pertenezca al intervalo
pertenezca al intervalo 
Todo lo anterior nos dice que para que se cumpla que  y
y  ,
,  debe de pertenecer a la intersección de los conjuntos que encontramos,
debe de pertenecer a la intersección de los conjuntos que encontramos,  y
y  , la cual es
, la cual es  .
.
Procedamos con nuestra segunda suposición principal, la cual es que  y
y  . Supongamos que
. Supongamos que  , primero, de nuevo debemos expresar este este polinomio de segundo orden como producto de expresiones de primer grado, esto es
, primero, de nuevo debemos expresar este este polinomio de segundo orden como producto de expresiones de primer grado, esto es

Para que esto sea negativo se debe cumplir también que  y
y  tengan signos opuestos. Suponiendo que
tengan signos opuestos. Suponiendo que 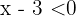 y
y  tenemos que
tenemos que  y
y  respectivamente, esto es,
respectivamente, esto es,  pertenece a la intersección de los intervalos
pertenece a la intersección de los intervalos  y
y  la cual es
la cual es  .
.
Ahora supongamos que  y
y  tenemos que
tenemos que  y
y  respectivamente, esto es,
respectivamente, esto es,  pertenece a la intersección de los intervalos
pertenece a la intersección de los intervalos  y
y  la cual es vacía. Así, la única forma de que
la cual es vacía. Así, la única forma de que  es que
es que  pertenezca al intervalo
pertenezca al intervalo 
También se tiene que  , debemos expresar este este polinomio de segundo orden como producto de expresiones de primer grado, esto es
, debemos expresar este este polinomio de segundo orden como producto de expresiones de primer grado, esto es

Para que esto sea positivo se debe cumplir también que  y
y  sean del mismo signo, esto es, que ambos sean positivos o ambos negativos. Suponiendo que ambos son negativos, tenemos que
sean del mismo signo, esto es, que ambos sean positivos o ambos negativos. Suponiendo que ambos son negativos, tenemos que  , entonces,
, entonces,  y
y 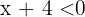 , entonces,
, entonces,  , esto es equivalente a decir que
, esto es equivalente a decir que  pertenece a la intersección de los intervalos
pertenece a la intersección de los intervalos  y
y  la cual es
la cual es  .
.
Ahora supongamos que  y
y  son positivos, tenemos que
son positivos, tenemos que  , entonces,
, entonces,  y
y  , entonces,
, entonces,  , esto es equivalente a decir que
, esto es equivalente a decir que  pertenece a la intersección de los intervalos
pertenece a la intersección de los intervalos  y
y  la cual es
la cual es  .
.
Así, para que se cumpla que  se debe tener que
se debe tener que  pertenezca a la unión de los dos intervalos que encontramos previamente, esto es,
pertenezca a la unión de los dos intervalos que encontramos previamente, esto es,  pertenece a
pertenece a  .
.
Por lo tanto tenemos que para que se cumpla que  y
y  ,
,  debe de pertenecer a la intersección de los conjuntos que encontramos,
debe de pertenecer a la intersección de los conjuntos que encontramos,  y
y  , la cual es vacía.
, la cual es vacía.
Nuestra solución final sería la unión de las dos soluciones para cada caso, sin embargo, como la última solución es el conjunto vacío, nuestra solución final es el conjunto  .
.


Notemos que

Para que la fracción sea igual a cero se tiene que cumpli que el numerador sea igual a cero, esto es  , por lo tanto
, por lo tanto  .
.
Tenemos que para que la fracción sea estrictamente negativa, se tiene que cumplir que el numerador y el denominador sean de signo opuesto. Primero supongamos que el numerador es positivo y el denominador negativo, por lo tanto  , esto es
, esto es  y
y  , por lo tanto
, por lo tanto  , esto quiere decir que
, esto quiere decir que  debe pertenecer a la intersección de los intervalos
debe pertenecer a la intersección de los intervalos  y
y  , la cual es
, la cual es  .
.
Ahora supongamos que el numerador es negativo y el denominador positivo, por lo tanto  , esto es
, esto es  y
y  , por lo tanto
, por lo tanto  , esto quiere decir que
, esto quiere decir que  debe pertenecer a la intersección de los intervalos
debe pertenecer a la intersección de los intervalos  y
y  , la cual es
, la cual es  .
.
Todo esto nos quiere decir que para que se cumpla que  , se tiene que
, se tiene que  debe pertenecer a la unión de los dos intervalos que obtuvimos y el punto
debe pertenecer a la unión de los dos intervalos que obtuvimos y el punto  , por lo tanto, el conjunto solución es
, por lo tanto, el conjunto solución es 

Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Ayúdame a resolver esto: una hamburguesa cuesta $5 y un gaseosa $2. Un cliente tiene máximo $20.¿Cuántas hamburguesas y gaseosas puede comprar?
✅ Datos
Precio de una hamburguesa = $5
Precio de una gaseosa = $2
Dinero máximo = $20
Buscamos todas las combinaciones posibles con:
5
ℎ
+
2
𝑔
≤
20
5h+2g≤20
donde h = hamburguesas (entero ≥ 0)
y g = gaseosas (entero ≥ 0)
✅ Probando cada cantidad de hamburguesas
Si compra 0 hamburguesas
Usa solo gaseosas:
$20 ÷ $2 = 10 gaseosas
➡ (0 hamburguesas, 10 gaseosas)
Si compra 1 hamburguesa
Costo hamburguesas: 1 × 5 = $5
Dinero restante: 20 – 5 = $15
Gaseosas: 15 ÷ 2 = 7.5 → solo se puede 7 gaseosas
➡ (1 hamburguesa, 7 gaseosas)
Si compra 2 hamburguesas
Costo: 2 × 5 = $10
Resto: 20 – 10 = $10
Gaseosas: 10 ÷ 2 = 5 gaseosas
➡ (2 hamburguesas, 5 gaseosas)
Si compra 3 hamburguesas
Costo: 3 × 5 = $15
Resto: 20 – 15 = $5
Gaseosas: 5 ÷ 2 = 2.5 → solo 2 gaseosas
➡ (3 hamburguesas, 2 gaseosas)
Si compra 4 hamburguesas
Costo: 4 × 5 = $20
Resto: 0
Gaseosas: 0
➡ (4 hamburguesas, 0 gaseosas)
Si compra 5 hamburguesas
5 × 5 = $25, eso pasa de $20 ❌ No se puede
✅ Todas las combinaciones válidas
Hamburguesas Gaseosas Total
0 10 0×5 + 10×2 = 20
1 7 1×5 + 7×2 = 19
2 5 2×5 + 5×2 = 20
3 2 3×5 + 2×2 = 19
4 0 4×5 + 0 = 20
✅ Estas son todas las combinaciones posibles con máximo $20.
3 hamburguesas y 2 gaseosas
En el ejercicio 9 de inecuaciones hay un error en el resultado, crec. Pone (-4,3) U (3,4) y creo que deberia ser (-4,-3)U(3,4). S no no lo comprendo.
Hola, fue un error nuestro discúlpanos ya se corrigió y gracias por tu ayuda.
48x+12>108
10(×+1)+<6(2×+1)