1 Arrastra cada gráfica a la inecuación de la que sea solución:
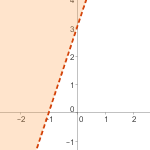
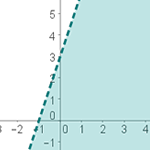
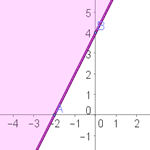
−3x + y ≥ 3
−3x + y < 3
−3x + y > 3
−3x + y ≤ 3
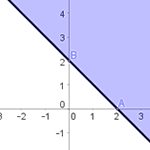
x + y ≥ 2
2x − y ≤ −4
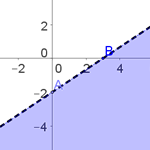
2x + 7y < 14
2x − 3y > 6
| −3x + y ≥ 3 | −3x + y < 3 |
 |  |
| −3x + y > 3 | −3x + y ≤ 3 |
 |  |
| x + y ≥ 2 | 2x − y ≤ −4 |
 |  |
| 2x + 7y < 14 | 2x − 3y > 6 |
 |  |
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Ayúdame a resolver esto: una hamburguesa cuesta $5 y un gaseosa $2. Un cliente tiene máximo $20.¿Cuántas hamburguesas y gaseosas puede comprar?
✅ Datos
Precio de una hamburguesa = $5
Precio de una gaseosa = $2
Dinero máximo = $20
Buscamos todas las combinaciones posibles con:
5
ℎ
+
2
𝑔
≤
20
5h+2g≤20
donde h = hamburguesas (entero ≥ 0)
y g = gaseosas (entero ≥ 0)
✅ Probando cada cantidad de hamburguesas
Si compra 0 hamburguesas
Usa solo gaseosas:
$20 ÷ $2 = 10 gaseosas
➡ (0 hamburguesas, 10 gaseosas)
Si compra 1 hamburguesa
Costo hamburguesas: 1 × 5 = $5
Dinero restante: 20 – 5 = $15
Gaseosas: 15 ÷ 2 = 7.5 → solo se puede 7 gaseosas
➡ (1 hamburguesa, 7 gaseosas)
Si compra 2 hamburguesas
Costo: 2 × 5 = $10
Resto: 20 – 10 = $10
Gaseosas: 10 ÷ 2 = 5 gaseosas
➡ (2 hamburguesas, 5 gaseosas)
Si compra 3 hamburguesas
Costo: 3 × 5 = $15
Resto: 20 – 15 = $5
Gaseosas: 5 ÷ 2 = 2.5 → solo 2 gaseosas
➡ (3 hamburguesas, 2 gaseosas)
Si compra 4 hamburguesas
Costo: 4 × 5 = $20
Resto: 0
Gaseosas: 0
➡ (4 hamburguesas, 0 gaseosas)
Si compra 5 hamburguesas
5 × 5 = $25, eso pasa de $20 ❌ No se puede
✅ Todas las combinaciones válidas
Hamburguesas Gaseosas Total
0 10 0×5 + 10×2 = 20
1 7 1×5 + 7×2 = 19
2 5 2×5 + 5×2 = 20
3 2 3×5 + 2×2 = 19
4 0 4×5 + 0 = 20
✅ Estas son todas las combinaciones posibles con máximo $20.
3 hamburguesas y 2 gaseosas
En el ejercicio 9 de inecuaciones hay un error en el resultado, crec. Pone (-4,3) U (3,4) y creo que deberia ser (-4,-3)U(3,4). S no no lo comprendo.
Hola, fue un error nuestro discúlpanos ya se corrigió y gracias por tu ayuda.
48x+12>108
10(×+1)+<6(2×+1)