Las inecuaciones de segundo y cuarto grado son herramientas matemáticas poderosas que nos permiten analizar y comprender una amplia variedad de situaciones en las que las desigualdades desempeñan un papel crucial. En estos ejercicios, exploraremos la resolución de inecuaciones de segundo y cuarto grado, lo que nos brindará la oportunidad de aplicar conceptos matemáticos avanzados y desarrollar habilidades analíticas sólidas.
¡Prepárate para sumergirte en el mundo de las inecuaciones de segundo y cuarto grado y fortalecer tus habilidades matemáticas!
Resuelve las inecuaciones siguientes
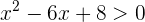
1 Igualamos el polinomio del primer miembro a cero, factorizamos y obtenemos
las raíces de la ecuación de segundo grado.

Igualando los factores a cero, se obtienen las raíces 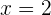 y
y 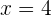
2 Las raíces dividen la recta real en tres intervalos: 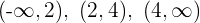
Los puntos extremos están en blanco porque no pertenecen a la
solución, ya que no es mayor o igual

3Tomamos un representante de cada intervalo y lo sustituimos en la inecuación


4 La solución está compuesta por los intervalos (o el intervalo)
que tengan el mismo signo que el polinomio.
Los intervalos son abiertos porque 2 y 4 no están incluidos en la solución
Así, la solución es 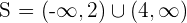
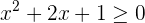
1 Igualamos el polinomio del primer miembro a cero, factorizamos y obtenemos
las raíces de la ecuación de segundo grado.

Igualando los factores a cero, se obtienen la raiz 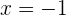
2 Como un número elevado al cuadrado es siempre positivo la solución es 
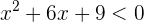
1 Igualamos el polinomio del primer miembro a cero, factorizamos y obtenemos
las raíces de la ecuación de segundo grado.
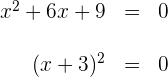
Igualando los factores a cero, se obtienen la raiz 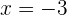
2 Como un número elevado al cuadrado es siempre positivo, la inecuación no tiene solución.

1 Igualamos el polinomio del primer miembro a cero y resolvemos la ecuación
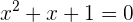
El polinomio no se puede factorizar por métodos elementales, por lo que estudiamos su discriminante

Como el discriminante es negativo, entonces no tiene raíces reales. Le damos al polinomio cualquier valor, por ejemplo 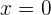
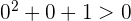
2 Como se cumple la desigualdad, la solución es 
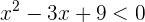
1 Igualamos el polinomio del primer miembro a cero y resolvemos la ecuación
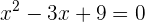
El polinomio no se puede factorizar por métodos elementales, por lo que estudiamos su discriminante
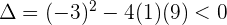
Como el discriminante es negativo, entonces no tiene raíces reales. Le damos al polinomio cualquier valor, por ejemplo 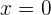

2 Como no se cumple la desigualdad, la inecuación no tiene solución
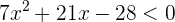
1 Igualamos el polinomio del primer miembro a cero, factorizamos y obtenemos
las raíces de la ecuación de segundo grado.

Igualando los factores a cero, se obtienen las raíces  y
y 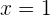
2 Las raíces dividen la recta real en tres intervalos: 
Las raíces no pertenecen a la solución, ya que no es menor o igual
3Tomamos un representante de cada intervalo y lo sustituimos en la inecuación


4 La solución está compuesta por los intervalos (o el intervalo)
que tengan el mismo signo que el polinomio.
Los intervalos son abiertos porque -4 y 1 no están incluidos en la solución
Así, la solución es 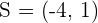
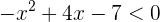
1 Igualamos el polinomio del primer miembro a cero y resolvemos la ecuación

El polinomio no se puede factorizar por métodos elementales, por lo que estudiamos su discriminante

Como el discriminante es negativo, entonces no tiene raíces reales. Le damos al polinomio cualquier valor, por ejemplo 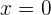
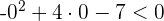
2 Como se cumple la desigualdad, la solución es 
Si no se hubiese cumplido la desigualdad no hubiese tenido solución.
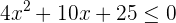
1 Igualamos el polinomio del primer miembro a cero y resolvemos la ecuación
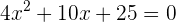
El polinomio no se puede factorizar por métodos elementales, por lo que estudiamos su discriminante
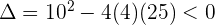
Como el discriminante es negativo, entonces no tiene raíces reales. Le damos al polinomio cualquier valor, por ejemplo 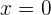
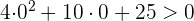
2 Como no se cumple la desigualdad, la inecuación no tiene solución
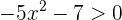
1 Igualamos el polinomio del primer miembro a cero y resolvemos la ecuación
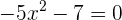
El polinomio no se puede factorizar por métodos elementales, por lo que estudiamos su discriminante
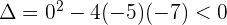
Como el discriminante es negativo, entonces no tiene raíces reales. Le damos al polinomio cualquier valor, por ejemplo 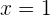
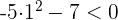
2 Como no se cumple la desigualdad, la inecuación no tiene solución
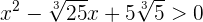
1 Igualamos el polinomio del primer miembro a cero y resolvemos la ecuación
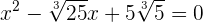
El polinomio no se puede factorizar por métodos elementales, por lo que estudiamos su discriminante
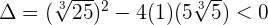
Como el discriminante es negativo, entonces no tiene raíces reales. Le damos al polinomio cualquier valor, por ejemplo 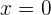

2 Como se cumple la desigualdad, la solución es 
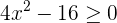
1 Obtener los valores críticos de la inecuación
Para esto igualamos a cero y factorizamos
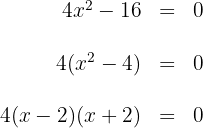
Igualando los factores a cero, se obtienen las raíces  . Estas raíces son soluciones (ya que al sustituir en la inecuación se cumple la igualdad)
. Estas raíces son soluciones (ya que al sustituir en la inecuación se cumple la igualdad)
2 Representar los valores críticos en la recta numérica
Como las raíces son 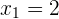 y
y 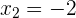 , la recta real se divide en los intervalos
, la recta real se divide en los intervalos  y
y 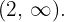
3 Tomamos los valores 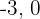 y
y  y los evaluamos en la inecuación
y los evaluamos en la inecuación


4Ya que la expresión cuadrática es positiva, la solución de la inecuación es la unión de dos intervalos: 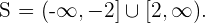
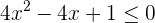
1 Obtener los valores críticos de la inecuación
Para esto igualamos a cero y factorizamos

Igualando el factor a cero, se obtiene la raíz 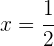
2 Como el binomio al cuadrado es negativo y el signo es menor o igual que, la inecuación tiene una única solución: 
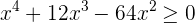
1 Obtener los valores críticos de la inecuación
Para esto igualamos a cero y factorizamos
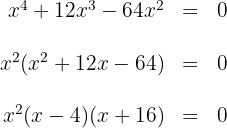
Igualando los factores a cero se obtienen las raíces  . Estas raíces son soluciones (ya que al sustituir en la inecuación se cumple la igualdad)
. Estas raíces son soluciones (ya que al sustituir en la inecuación se cumple la igualdad)
2 Representar los valores críticos en la recta numérica
Como las raíces son 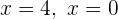 y
y  , la recta real se divide en los intervalos
, la recta real se divide en los intervalos  y
y 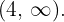
3Tomamos los valores 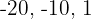 y
y  y los sustituimos en la inecuación
y los sustituimos en la inecuación
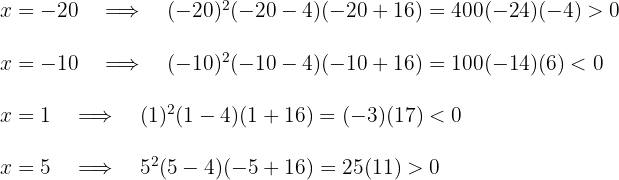

4 Como la expresión cuadrática es positiva, la solución es la unión de los intervalos 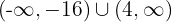 y los valores críticos. Así, la solución es
y los valores críticos. Así, la solución es 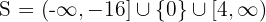
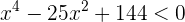
1 Obtener los valores críticos de la inecuación
Para esto igualamos a cero y factorizamos
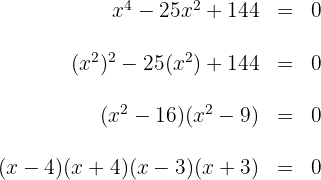
Igualando los factores a cero se obtienen las raíces 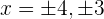 .
.
2 Representar los valores críticos en la recta numérica
Como las raíces son  , la recta real se divide en los intervalos
, la recta real se divide en los intervalos 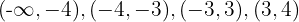 y
y 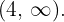
3 Tomamos los valores  y
y  y los sustituimos en la inecuación
y los sustituimos en la inecuación
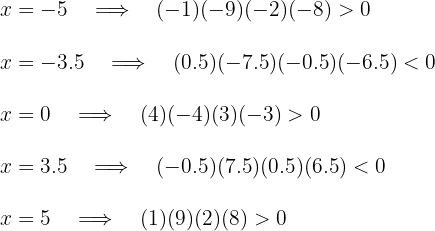

4 Como la expresión cuadrática es negativa, la solución es la unión de los intervalos 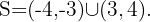

1 Obtener los valores críticos de la inecuación
Para esto igualamos a cero y factorizamos

Como el binomio 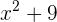 siempre es mayor a cero para cualquer valor de
siempre es mayor a cero para cualquer valor de  , únicamente se consideran los binomios lineales para calcular los valores críticos. Así,
, únicamente se consideran los binomios lineales para calcular los valores críticos. Así,  son las raíces buscadas. Estas raíces son soluciones (ya que al sustituir en la inecuación se cumple la igualdad)
son las raíces buscadas. Estas raíces son soluciones (ya que al sustituir en la inecuación se cumple la igualdad)
2 Representar los valores críticos en la recta numérica
Como las raíces son  , la recta real se divide en los intervalos
, la recta real se divide en los intervalos 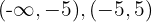 y
y 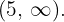
3 Tomamos los valores  y
y  , sustituimos en la inecuación
, sustituimos en la inecuación


4 Como la expresión cuadrática es positiva o cero, la solución es la unión de los intervalos y los valores críticos, esto es, 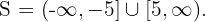
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Ayúdame a resolver esto: una hamburguesa cuesta $5 y un gaseosa $2. Un cliente tiene máximo $20.¿Cuántas hamburguesas y gaseosas puede comprar?
✅ Datos
Precio de una hamburguesa = $5
Precio de una gaseosa = $2
Dinero máximo = $20
Buscamos todas las combinaciones posibles con:
5
ℎ
+
2
𝑔
≤
20
5h+2g≤20
donde h = hamburguesas (entero ≥ 0)
y g = gaseosas (entero ≥ 0)
✅ Probando cada cantidad de hamburguesas
Si compra 0 hamburguesas
Usa solo gaseosas:
$20 ÷ $2 = 10 gaseosas
➡ (0 hamburguesas, 10 gaseosas)
Si compra 1 hamburguesa
Costo hamburguesas: 1 × 5 = $5
Dinero restante: 20 – 5 = $15
Gaseosas: 15 ÷ 2 = 7.5 → solo se puede 7 gaseosas
➡ (1 hamburguesa, 7 gaseosas)
Si compra 2 hamburguesas
Costo: 2 × 5 = $10
Resto: 20 – 10 = $10
Gaseosas: 10 ÷ 2 = 5 gaseosas
➡ (2 hamburguesas, 5 gaseosas)
Si compra 3 hamburguesas
Costo: 3 × 5 = $15
Resto: 20 – 15 = $5
Gaseosas: 5 ÷ 2 = 2.5 → solo 2 gaseosas
➡ (3 hamburguesas, 2 gaseosas)
Si compra 4 hamburguesas
Costo: 4 × 5 = $20
Resto: 0
Gaseosas: 0
➡ (4 hamburguesas, 0 gaseosas)
Si compra 5 hamburguesas
5 × 5 = $25, eso pasa de $20 ❌ No se puede
✅ Todas las combinaciones válidas
Hamburguesas Gaseosas Total
0 10 0×5 + 10×2 = 20
1 7 1×5 + 7×2 = 19
2 5 2×5 + 5×2 = 20
3 2 3×5 + 2×2 = 19
4 0 4×5 + 0 = 20
✅ Estas son todas las combinaciones posibles con máximo $20.
3 hamburguesas y 2 gaseosas
En el ejercicio 9 de inecuaciones hay un error en el resultado, crec. Pone (-4,3) U (3,4) y creo que deberia ser (-4,-3)U(3,4). S no no lo comprendo.
Hola, fue un error nuestro discúlpanos ya se corrigió y gracias por tu ayuda.
48x+12>108
10(×+1)+<6(2×+1)