Capítulos
Reparto directamente proporcional
Recordemos que un reparto directamente proporcional consiste en repartir una cantidad entre varias partes de manera que lo que reciba cada una de las partes involucradas sea directamente proporcional a la cantidad aportada por cada una.
Ejercicios interactivos de repartos directamente proporcionales
Resuelve los siguientes problemas de repartos directamente proporcionales y anota tus respuestas en los espacios correspondientes, al finalizar los problemas presiona corregir al final de la sección para verificar si tus respuestas son correctas.
1 Se quiere repartir un premio de 1000 € en cheques para libros a los tres mejores goleadores del equipo de fútbol del instituto de manera proporcional a los goles marcados en la última temporada. Sabiendo que Pedro marcó 53 goles, Marta 39 goles y Adolfo 33, ¿de cuánto dinero es el cheque que le corresponde a cada uno?
El cheque de Pedro es de €,
Este campo es obligatorio.
el cheque de Marta es de €
Este campo es obligatorio.
y el cheque de Adolfo es de €.
Este campo es obligatorio.
e trata de un reparto proporcional, porque a más goles más dinero.
El reparto proporcional es: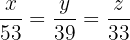 
donde 
es la cantidad de dinero que le corresponde a Pedro, Marta y Adolfo, respectivamente.
Ahora bien, por la propiedad de las razones iguales: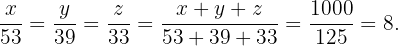 
Y resolviendo para cada uno obtenemos
Pedro:
Marta:
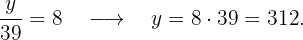
Adolfo:
2 En un campamento se reparten 300 litros de agua a cuatro bungalows que se han quedado sin suministro de agua potable. El reparto se hace de manera proporcional al número de chicos y chicas de cada bungalow. Eva convive con 9 compañeros, Mario con 5, Paula con 6 y Leo también vive con 6 compañeros.
¿Cuántos litros de agua corresponde al bungalow de Eva? l
Este campo es obligatorio.
¿Cuántos litros de agua corresponde al bungalow de Mario? l
Este campo es obligatorio.
¿Cuántos litros de agua corresponde al bungalow de Paula? l
Este campo es obligatorio.
¿Cuántos litros de agua corresponde al bungalow de Leo? l
Este campo es obligatorio.
Se trata de un reparto proporcional, porque a más compañeros más litros de agua.
Notemos que en el bungalow de Eva hay en total 10 personas, ya que convive con 9 y con ella son 10 , en el de Mario en total son 6, y en los de Paula y Leo 7.
El reparto proporcional es: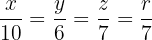 
donde 
son los litros de agua que le corresponde al bungalow de Eva, Mario, Paula y Leo, respectivamente.
Por la propiedad de las razones iguales: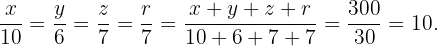 
Resolviendo obtenemos
Eva:
Mario:
Paula:
Leo:
3 Andrea y José decidieron comprar juntos un billete de lotería de 14 euros, Andrea pagó 9 euros del boleto y José los 5 euros faltantes. Después de unos días les notificaron que su boleto había ganado un premio de 308 euros. Si se reparten el premio de manera proporcional a lo que pagaron ¿Cuánto le corresponde a cada uno?
¿Cuánto dinero le corresponde a Andrea? euros,
Este campo es obligatorio.
¿Cuánto dinero le corresponde a José? euros.
Este campo es obligatorio.
Se trata de un reparto proporcional, donde quien más paga mayor recompensa se lleva .
El reparto proporcional es:
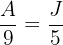donde 
es el dinero correspondiente de Andrea y José respectivamente.
Por la propiedad de las razones iguales:
Resolviendo obtenemos
Andrea:
José:
4 Dos constructores ganaron 500 € por cierto trabajo en el cual uno de ellos trabajo 4 días y el otro 5.
¿Cuánto dinero le corresponde al constructor que trabajó durante 4 días? €
Este campo es obligatorio.
¿Y al que trabajó 5 días? € .
Este campo es obligatorio.
Se trata de un reparto proporcional, donde gana más quien trabaja más días.
El reparto proporcional es:
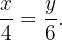
Por la propiedad de las razones iguales:
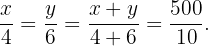
Resolviendo obtenemos
Primer constructor:
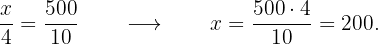
Segundo constructor:
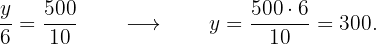
5 Fernando repartirá 150 dólares entre sus 4 sobrinos de forma directamente proporcional a las edades de cada uno de ellos. Si las edades de sus sobrinos son 5, 7, 8 y 10 años ¿cuánto le corresponde a cada sobrino?
Al sobrino de 5 años le corresponden dólares,
Este campo es obligatorio.
al de 7 años le tocan dólares,
Este campo es obligatorio.
al sobrino de 8 años dólares,
Este campo es obligatorio.
y finalmente al sobrino con 10 años dólares.
Este campo es obligatorio.
Se trata de un reparto proporcional, donde a más edad más dinero.
El reparto proporcional es:
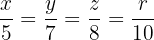donde 
es la cantidad de dinero que le corresponde a cada sobrino.
Ahora bien, por la propiedad de las razones iguales:
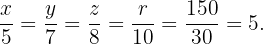
Y resolviendo para cada uno obtenemos
Sobrino de 5 años:
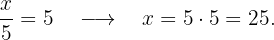
Sobrino de 7 años:
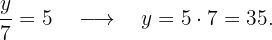
Sobrino de 8 años:
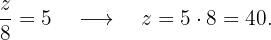
Sobrino de 10 años:
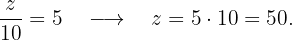
6 En una sesión para una revista fotográfica, tres fotógrafos cobraron 6720 euros. En la revista, 14 fotos eran del fotógrafo 1 , 18 del fotógrafo 2 y 24 del fotógrafo 3. ¿Qué cantidad de euros le corresponde a cada uno?
Al fotógrafo 1 le corresponden euros,
Este campo es obligatorio.
al fotógrafo 2 le tocan euros,
Este campo es obligatorio.
y al fotógrafo 3 le pertenecen euros.
Este campo es obligatorio.
Se trata de un reparto proporcional, porque a más fotógrafias más dinero correspondiente.
El reparto proporcional es:
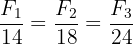donde 
cantidad de dinero que le corresponde al Fotógrafo 1, 2 y 3 respectivamente.
Ahora bien, por la propiedad de las razones iguales:
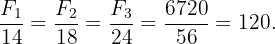
Y resolviendo para cada uno obtenemos
Fotógrafo 1:
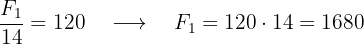
Fotógrafo 2:
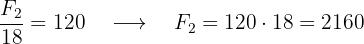
Fotógrafo 3:
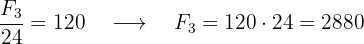
7 Ricardo reparte cierta cantidad de dinero entre sus tres hijas de manera que sea proporcional a la cantidad de hijos que cada una tiene. La mayor tiene 3 hijos, la segunda hija tiene 2 niños y la tercera 5 hijos. Si 1a tercer hija ha recibido 700 dólares más que la primera ¿Cuánto dinero le corresponde a cada una? ¿Cuánto dinero repartió Ricardo en total?
A la hija mayor le corresponden dolares,
Este campo es obligatorio.
a la segunda hija
Este campo es obligatorio.
y a la hija menor dólares.
Este campo es obligatorio.
¿Cuánto dinero repartió Ricardo en total? dólares.
Este campo es obligatorio.
Se trata de un reparto proporcional, donde a más hijos más dinero correspondiente.
Sea 
la cantidad de dinero que recibe cada una de las hijas, entonces el reparto proporcional es:
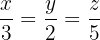
Sabemos que la hija menor recibió 700 dólares más que la hija mayor, entonces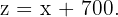 
Sustituyendo 
en el reparto proporcional obtenemos
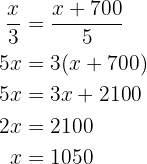
es decir, a la hija mayor le corresponden 1050 dólares. De aquí es sencillo calcular cuanto le corresponde a la hija menor, pues serian 
Por otra parte del reparto proporcional tenemos que
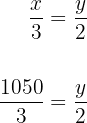
entonces podemos calcular lo que le corresponde a la segunda hija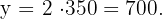 
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cuánto se debe depositar cada fin de semestre si usted quiere acumular Bs 10000 al cabo de 4 años conociendo que la entidad financiera reconoce un interés del 12% anual
esta mal la mayoria de ejercicios la cual se confunde en el mismo ejercicios ep e ip
Hola puedes hacernos el favor de mencionar los ejercicios que están mal para poder corregirlos y así evitar confusiones.
Buenos días, el ejercicio 1 está mal si la relación fuera directa entre las variables que no lo e como muestra ahí daría 400kg. La respuesta para mí es que: la relación de las variables es indirecta lo que no sé cómo llega a los 25000. No llego a ese número.
La empresa A1 tal pone en la bolsa de valores $134 acciones por 130 c/u para mantenerlas 3 años
La empresa A2 las compra y las pone nuevamente en la bolsa de valores a un interes simple de 30% por los 3 años
La tercera empresa compra estas acciones por 5 años
Durante el primer semestre la empresa A2 ve que las acciones compradas bajan a $100 podría resolverlo con las cuentas
Hola tu razonamiento es correcto si a mayor tamaño de la rueda, mas vueltas da, pero no es así, pues las ruedas grandes dan menos vueltas que las ruedas pequeñas, por eso se usa razones inversamente proporcionales.