
Entender los porcentajes
El porcentaje nos indica un tanto de cada 100 unidades, entonces, el 7% de alguna cantidad implica que de cada 100 unidades solo se toman 7, en los ejercicios siguientes, esto se expresa como
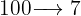
Para facilitarnos el trabajo lo primero que debemos hacer es identificar el elemento que voy a calcular, este puede ser alguna cantidad o algún porcentaje, el elemento que calculemos será sustituido por la variable x en la tabla que se muestra a continuación:

Para calcular el valor, solo necesitamos hacer una proporcionalidad, en el mismo orden que tenemos los datos previamente acomodados:

es decir:

Al remplazar alguno de los valores con x, sólo bastara despejar x, por ejemplo, supongamos que queremos calcular el porcentaje, entonces, sustituimos "porcentaje" por x:
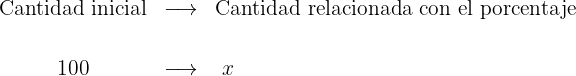
nuestra relación seria de la forma:
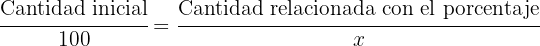
y al despejarla obtendríamos:
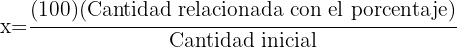
De igual modo, si escribimos los datos en otro orden:

podemos usar nuestra relación de la siguiente manera:
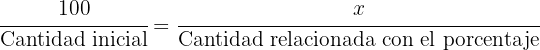
Y al despejarse, queda de la misma manera que la anterior.
Problemas de la vida cotidiana usando porcentajes
De los 800 alumnos de un colegio, han ido de viaje 600. ¿Qué porcentaje de alumnos ha ido de viaje?
1Identificamos y ordenamos los datos, sustituyendo el dato a calcular con x:
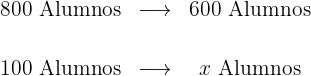
2Establecemos la relación de los datos, despejamos x y resolvemos:


Al adquirir un vehículo cuyo precio es de 8800 €, nos hacen un descuento del 7.5%. ¿Cuánto hay que pagar por el vehículo?
1Identificamos y ordenamos los datos, sustituyendo el dato a calcular con x:

2Establecemos la relación de los datos, despejamos x y resolvemos:


3 Restamos el valor de 'x' del costo original

4 También se puede calcular directamente del siguiente modo:
Hay un descuento del 7.5%, es decir, que solo estamos pagando el 92.5% del total, así que en lugar de estar 7.5 de cada 100, solo debemos calcular el 92.5% o bien, los 92.5 de cada 100:
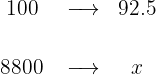
5Establecemos la relación de los datos, despejamos x y resolvemos:
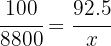
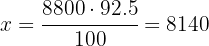
El precio de un ordenador es de 1200 € sin IVA. ¿Cuánto hay que pagar por él si el IVA es del 16%?
1Debido al IVA hay un recargo del 16%, es decir, de cada 100 € pagamos 16 € más, por tanto en vez de los 100 € pagamos pagamos 116 €
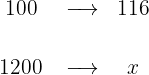
2Establecemos la relación de los datos, despejamos x y resolvemos:


Al comprar un monitor que cuesta 450 € nos hacen un descuento del 8%. ¿Cuánto tenemos que pagar?
1 Hay un descuento del 8%, es decir, de cada 100 € pagamos 8 € menos por tanto en vez de los 100 € pagamos pagamos 92 €

2Establecemos la relación de los datos, despejamos x y resolvemos:

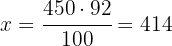
Se vende un artículo con una ganancia del 15% sobre el precio de costo. Si se ha comprado en 80 €. Halla el precio de venta.
1 Identificamos y ordenamos los datos, sustituyendo el dato a calcular con x:
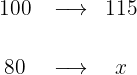
2Establecemos la relación de los datos, despejamos x y resolvemos:


¿Cuál será el precio que hemos de marcar en un artículo cuya compra ha sido de 180 € para ganar al venderlo el 10%?
1Precio de compra es de 180 € y pretendemos ganar el 10%

2Establecemos la relación de los datos, despejamos x y resolvemos:

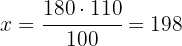
Queremos vender unos zapatos por una aplicación de ropa de segunda mano. Los zapatos los compramos por 280 € y ahora queremos venderlos un 12% más baratos. ¿Qué precio deberemos marcar en la aplicación?
1Tenemos
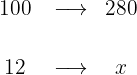
2Establecemos la relación de los datos, despejamos x y resolvemos:


3 Ahora tenemos el 12% de 280, necesitamos saber qué precio pondremos en la aplicación. Para ello, restamos:

Para vender los zapatos un 12% más baratos, los venderemos en la aplicación por 
Se vende un objeto perdiendo el 20% sobre el precio de compra. Hallar el precio de venta del citado artículo cuyo valor de compra fue de 150 €.
1 Si el precio de compra es 100 € y se pierde el 20%, el precio de venta será de 80 €
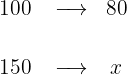
2Establecemos la relación de los datos, despejamos x y resolvemos:

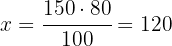
Un concesionario tiene 120 coches, el 35% de ellos son blancos y el 5% rojos. ¿Cuántos coches de cada color hay?
Tenemos que calcular el 35% y el 5% de 120. Como el total de coches es 120, lo identificamos con el 100%.
1 Calculamos primero la cantidad de coches blancos
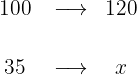
Es decir,
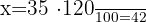
2Veamos ahora la cantidad de coches rojos
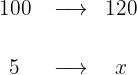
Por tanto, la cantidad de coches rojos es

De los 684 lanzamientos que realizó Daniel, falló 513. ¿Qué porcentaje de lanzamientos fallidos tiene Daniel?
1 Identificamos 684 con el 100% y queremos ver que porcentaje representa 513

2Establecemos la relación de los datos, despejamos x y resolvemos:
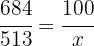
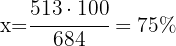
El 18% de los árboles del jardín de la plaza mayor son almendros y el resto son naranjos. Si en la plaza 45 almendros, ¿Cuántos árboles hay en total en la plaza?
1 Sólo tenemos que identificar el 18% con 45 para calcular el 100%:
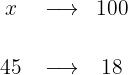
2Establecemos la relación de los datos, despejamos x y resolvemos:
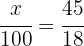
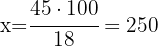
Es decir, hay un total de 250 arboles.
En una tienda quieren rebajar 5€ el precio de un libro de 25€. ¿Qué porcentaje de descuento estarían aplicando?
1 Puesto que los 25€ son el 100%,
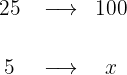
2Establecemos la relación de los datos, despejamos x y resolvemos:
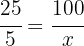
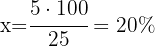
Es decir, si rebajan 5€, estarían aplicando un descuento del 20% del precio inicial.
Adrián medía 165cm, pero en un año ha crecido un 8%. ¿Cuánto mide ahora Adrián? ¿Cuántos centímetros ha crecido?
1 Los 165cm son el 100% de la estatura de Adrián. Al crecer un 8%, ahora su estatura es el 108% de 165cm:
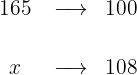
2Establecemos la relación de los datos, despejamos x y resolvemos:
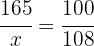
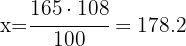
Adrián mide 178.2cm, es decir, creció 13.2cm.
Lara acertó el 85% de las preguntas del test de inglés. Si el test tenía un total de 160 preguntas, ¿en cuántas preguntas no acertó?
1 Identificamos 160 con el 100%. Como acertó el 85%, no acertó el 15%. Por tanto, vamos a calcular el 15% de 160:

2Establecemos la relación de los datos, despejamos x y resolvemos:

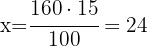
Por tanto, Lara no acertó 24 preguntas.
En un aula de 80 alumnos, el 45% son niñas, de las cuales, el 25% son rubias. ¿Cuántas niñas rubias hay en el aula?
1 Para calcular el número de niñas rubias necesitamos calcular el número total de niñas en el aula, en este caso identificamos los 80 alumnos como el 100%
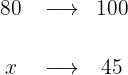
Por tanto
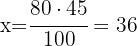
2Ahora bien, calculemos el total de niñas rubias de las 36, en este caso el 100% es el total de niñas
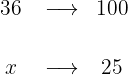
entonces
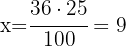
En el aula hay 9 niñas rubias.
En Superprof contamos con los mejores profesionales así que seguro que encuentras tu profesor de mates ideal. ¿Que prefieres un profesor de matematicas online? También tenemos en Superprof.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en la numero dos, el desarrollo, junto con la respuesta esta mal, ya que no se esta contemplando el factor tiempo, que claramente se ve al principio de la formula
Hola si te refieres al problema de pintar una casa, entendemos que no parezca clara esta técnica, también se puede platear de la siguiente forma, por 25 horas de trabajo se paga 500 euros, y resolver el problema en dos casos, cuanto equivale 10 horas y después 15 horas en euros, obteniendo los mismos resultados.
Cuánto se debe depositar cada fin de semestre si usted quiere acumular Bs 10000 al cabo de 4 años conociendo que la entidad financiera reconoce un interés del 12% anual
La numero 7 la respuesta sare de verded y la el numero es que sale de rojo
Hola, si tienes razón y vamos a trabajar en ello, te agradecemos.
esta mal la mayoria de ejercicios la cual se confunde en el mismo ejercicios ep e ip
Hola puedes hacernos el favor de mencionar los ejercicios que están mal para poder corregirlos y así evitar confusiones.
Hola tu razonamiento es correcto si a mayor tamaño de la rueda, mas vueltas da, pero no es así, pues las ruedas grandes dan menos vueltas que las ruedas pequeñas, por eso se usa razones inversamente proporcionales.