Capítulos

Conceptos preliminares
1. Magnitud . Una magnitud es una propiedad que se puede medir numéricamente. Por ejemplo, el peso, la masa, la longitud, el volumen, el tiempo, etc. Todas estas son magnitudes de sistemas físicos.
2. Razón. Definimos la razón entre dos cantidades comparables como el cociente de éstas, expresado como fracción (o como decimal o entero si es más conveniente). Así, la razón entre una cantidad  y una cantidad
y una cantidad  la expresamos como
la expresamos como

y se lee como  es a
es a 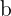 .
.
Al numerador de la fracción se le conoce como antecedente y al numerador como consecuente.
Ejemplo:
Luis dedica 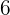 horas diarias al estudio y
horas diarias al estudio y  horas diarias a jugar. ¿Cuál sería la razón entre las horas de estudio y las horas de juego que dedica diariamente Luis?
horas diarias a jugar. ¿Cuál sería la razón entre las horas de estudio y las horas de juego que dedica diariamente Luis?
En este caso el antecedente sería  , mientras que el consecuente sería
, mientras que el consecuente sería 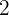 . Entonces, la razón estaría dada por
. Entonces, la razón estaría dada por

y que 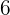 es a
es a 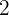 . Así, la razón nos dice que, por cada hora que dedica Luis al jugar, le dedica tres horas a estudiar (la razón es
. Así, la razón nos dice que, por cada hora que dedica Luis al jugar, le dedica tres horas a estudiar (la razón es 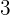 ).
).
Proporción
¿Y si pruebas nuestras clases particulares matematicas madrid?
Una proporción es una igualdad entre dos razones. Así, dadas dos razones  y
y  , tendríamos una proporción si
, tendríamos una proporción si

La proporción de arriba se lee  es a
es a  como
como 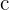 es a
es a  . Además, a
. Además, a  y
y  se les conoce como extremos, mientras que a
se les conoce como extremos, mientras que a  y
y 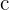 se les conoce como medios.
se les conoce como medios.
Cualquier proporción cumple que el producto de los extremos es igual al producto de los medios. Así, tendríamos que 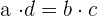 .
.
Ejemplo. Consideremos las razones  y
y  . Notemos que
. Notemos que
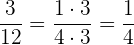
Así, tenemos una proporción,
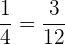 .
.
Para este ejemplo, tenemos que los extremos son  y
y  , mientras que los medios son
, mientras que los medios son 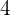 y
y 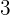 .Notemos que el producto de los extremos es
.Notemos que el producto de los extremos es

y el producto de los medios es
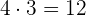 .
.
Ambos productos dan el mismo resultado.
En una serie de razones iguales (serie de proporciones), por ejemplo,
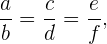
se tiene que la suma de los antecedentes dividida entre la suma de los consecuentes de las razones de la serie es igual a una cualquiera de las razones.
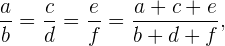
Si en una proporción cambiamos de lugar los antecedentes y los consecuentes, seguirá existiendo una proporción. En otras palabras, si dos razones son iguales
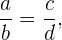
entonces sus recíprocos también serán iguales
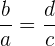 .
.
Ejemplo:
Retomemos la proporción del ejemplo anterior,
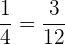 .
.
Tomando el recíproco de la primera razón, tenemos
 .
.
Tomando el recíproco de la segunda razón, tenemos
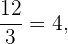
por lo tanto, tenemos que el recíproco de las razones también son iguales,
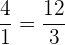 .
.
Cuarto proporcional
¿Has probado nuestras clases de matematicas online?
Un cuarto proporcional es cualquier de los términos de una proporción. Para calcularlo tenemos que considerar dos casos:
- Si este se encuentra en numerador de la razón,
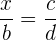 .
.
Entonces, se calcula como
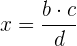 .
.
-
Si este se encuentra en denominador de la razón,
 .
.Entonces, se calcula como
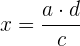 .
.
Notemos que simplemente es despejar el cuarto proporcional.
Ejemplo. Consideremos la proporción
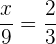 .
.
¿Cuánto vale el cuarto proporcional dado por el término 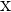 ? Procedamos a calcularlo
? Procedamos a calcularlo
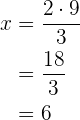
Medio proporcional
Una proporción es continua si sus medios son iguales,
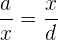 .
.
En este caso, al cuarto proporcional correspondiente a los medios se conoce como medio proporcional. Además, podemos calcularlo como
 .
.
Ejemplo:
Consideremos la proporción
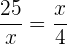 .
.
¿Cuánto vale el medio proporcional dado por el término 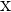 ? Procedamos a calcularlo
? Procedamos a calcularlo

Tercero proporcional
En una proporción continua, se denomina tercero proporcional a cada uno de los términos desiguales.
Para calcular los terceros proporcionales debemos considerar dos casos:
- Si este se encuentra en numerador de la razón,
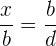 .
.
Entonces, se calcula como
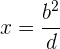 .
.
-
Si este se encuentra en denominador de la razón,
 .
.Entonces, se calcula como
 .
.
Notemos que en cualquier caso, el tercero proporcional es igual al cuadrado del medio proporcional dividido por el otro tercero proporcional.
Ejemplo:
Consideremos la proporción
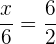 .
.
¿Cuánto vale el tercero proporcional dado por el término 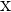 ? Procedamos a calcularlo
? Procedamos a calcularlo

Magnitudes directamente proporcionales
Dos magnitudes son directamente proporcionales cuando, al multiplicar una de ellas por un número cualquiera, la otra queda multiplicada por el mismo número. Igualmente, dos magnitudes son directamente proporcionales si, al dividir una por cualquier número, entonces la otra queda dividida por el mismo número.
Se establece una relación de proporcionalidad directa entre dos magnitudes cuando:
- A más cantidad de la primera magnitud, corresponde más cantidad en la segunda magnitud, en la misma proporción.
- A menos cantidad en la primera magnitud, corresponde menos cantidad en la segunda magnitud, en la misma proporción.
Otra manera de determinar si dos magnitudes son directamente proporcionales es por medio de su cociente. El cociente entre dos magnitudes directamente proporcionales siempre es constante.
Ejemplo:
El peso de un producto y su precio son dos magnitudes directamente proporcionales.
Observemos que si  de tomates cuesta
de tomates cuesta  €, entonces:
€, entonces:
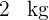 de tomates costará
de tomates costará 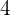 €
€ de tomates costará
de tomates costará  €
€
Regla de tres simple y directa
¿Necesitas clases particulares matematicas?
La regla de tres simple y directa consiste en una relación de cantidades con proporcionalidad directa, que se da cuando dadas dos cantidades correspondientes a magnitudes directamente proporcionales, se debe calcular la cantidad de una de estas magnitudes correspondiente a una cantidad dada de la otra magnitud.
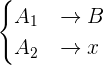

Ejemplo. Un automóvil recorre  en
en  horas. ¿Cuántos kilómetros habrá recorrido en
horas. ¿Cuántos kilómetros habrá recorrido en  horas?
horas?
Notemos que son magnitudes directamente proporcionales, esto ya que a menos horas menos kilómetros recorrerá. Procedamos a hacer el cálculo:
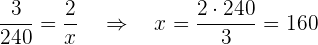
Por lo tanto, en  horas habrá recorrido
horas habrá recorrido  .
.
Repartos directamente proporcionales
Un reparto directamente proporcional consiste en que dadas unas magnitudes de un mismo tipo y una magnitud total, calcular la parte correspondiente a cada una de las magnitudes dadas. Así, si 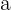 ,
,  y
y 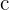 son magnitudes del mismo tipo, y tenemos una magnitud total
son magnitudes del mismo tipo, y tenemos una magnitud total  , queremos encontrar magnitudes
, queremos encontrar magnitudes 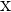 ,
, 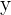 y
y 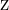 tal que
tal que  y
y

Ejemplo. Un abuelo reparte 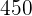 € entre sus tres nietos de
€ entre sus tres nietos de 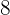 ,
,  y
y 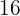 años de edad; proporcionalmente a sus edades. ¿Cuánto corresponde a cada uno?
años de edad; proporcionalmente a sus edades. ¿Cuánto corresponde a cada uno?
Primero, llamamos 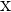 ,
, 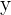 y
y 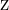 a las cantidades que le corresponde a cada uno.
a las cantidades que le corresponde a cada uno.
El reparto proporcional es:

Cada nieto recibirá:
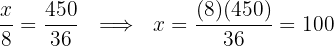

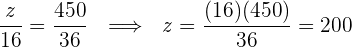
Porcentajes
Un porcentaje es un tipo de regla de tres directa en el que una de las cantidades es 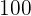 .
.
Ejemplo. Un amigo tiene  € , le piden que le de el
€ , le piden que le de el 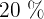 a su hermano. ¿Cuántos euros le dará a su hermano?
a su hermano. ¿Cuántos euros le dará a su hermano?
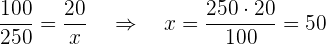
Por lo tanto, le debe de dar 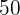 € a su hermano.
€ a su hermano.
Magnitudes inversamente proporcionales
Dos magnitudes son inversamente proporcionales si al aumentar una, disminuye la otra en la misma proporción. Esto pasa cuando:
-
- Al multiplicar una de ellas por un número cualquiera, la otra queda dividida por el mismo número.
- Al dividir una de ellas por un número cualquiera, la otra queda multiplicada por el mismo número.
Se establece una relación de proporcionalidad inversa entre dos magnitudes cuando:
-
- A más corresponde menos.
- A menos corresponde más.
Ejemplo:
Supongamos que  pintores tardan
pintores tardan 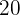 días en pintar un mural. Es claro que si duplicamos el número de pintores, el tiempo que se necesita para pintar la barda se reduce a la mitad, es decir
días en pintar un mural. Es claro que si duplicamos el número de pintores, el tiempo que se necesita para pintar la barda se reduce a la mitad, es decir 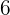 pintores tardarán
pintores tardarán 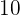 días.
días.
De igual manera si reducimos el número de pintores a una tercera parte, el tiempo requerido para realizar la misma tarea será el triple. Es decir  pintor, tardaría
pintor, tardaría  días. Al saber lo que tarda un pintor, ya podemos completar una tabla como la siguiente:
días. Al saber lo que tarda un pintor, ya podemos completar una tabla como la siguiente:
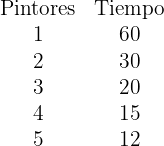
Así que el número de personas que realizan una tarea es inversamente proporcional al tiempo que tardan.
Regla de tres simple inversa
La regla de tres simple e inversa consiste en una relación de cantidades con proporcionalidad inversa, que se da cuando dadas dos cantidades correspondientes a magnitudes inversamente proporcionales, se debe calcular la cantidad de una de estas magnitudes correspondiente a una cantidad dada de la otra magnitud.
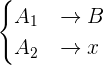
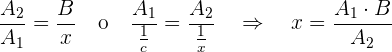
Ejemplo:
Un grifo que mana 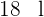 de agua por minuto tarda
de agua por minuto tarda 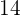 horas en llenar un depósito. ¿Cuánto tardaría si su caudal fuera de
horas en llenar un depósito. ¿Cuánto tardaría si su caudal fuera de  por minuto?
por minuto?
Notemos que son magnitudes inversamente proporcionales, ya que a menos litros por minuto tardará más tiempo en llenar el depósito. Procedamos a resolver. Tenemos la relación
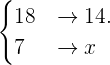
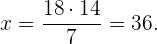
Por lo tanto, si el caudal fuera de  por minuto, tardaría
por minuto, tardaría 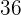 horas.
horas.
Repartos inversamente proporcionales
Un reparto inversamente proporcional consiste en que dadas unas magnitudes de un mismo tipo y una magnitud total, debemos hacer un reparto directamente proporcional a los recíprocos de las magnitudes. Así, si 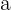 ,
,  y
y 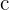 son magnitudes del mismo tipo, y tenemos una magnitud total
son magnitudes del mismo tipo, y tenemos una magnitud total  , queremos encontrar magnitudes
, queremos encontrar magnitudes 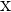 ,
, 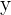 y
y 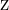 tal que
tal que  y
y
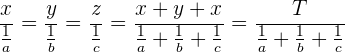
Ejemplo:
Durante la lectura de un testamento, el abogado del señor Rodríguez leyó el siguiente párrafo sobre la herencia que quería dejarle a sus hijos: “… A mis hijos: Hugo, Paco y Luis, les quiero repartir la cantidad de 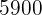 €. El reparto deberá hacerse de forma que reciban una cantidad inversamente proporcional a la edad que tengan al momento de mi fallecimiento…” Si las edades de Hugo, Paco y Luis son
€. El reparto deberá hacerse de forma que reciban una cantidad inversamente proporcional a la edad que tengan al momento de mi fallecimiento…” Si las edades de Hugo, Paco y Luis son 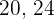 y
y  años, respectivamente. ¿Cuánto deberá recibir cada uno?
años, respectivamente. ¿Cuánto deberá recibir cada uno?
Debido a que el reparto se realizará de manera inversamente proporcional, al hijo menor le tocará una cantidad mayor de la herencia, mientras que al hijo mayor le tocará una cantidad menor. Esto se puede resolver obteniendo los inversos de las edades y realizando un reparto directamente proporcional con ellos y la cantidad total.
1 Obtenemos los inversos de las edades y convertimos las fracciones a denominador común (recuerda que puedes emplear el mcm).
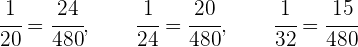
2 Realizamos un reparto directamente proporcional de estas fracciones:
 y
y 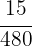 .
.
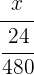 =
= 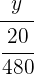 =
= 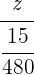 =
= 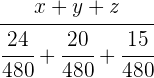 =
= 
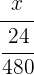 =
=  ⇒
⇒ 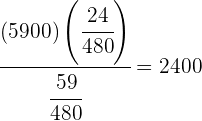 €
€
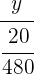 =
=  ⇒
⇒  €
€
 =
=  ⇒
⇒ 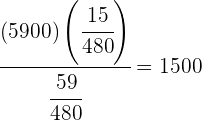 €
€
Así, Hugo recibirá  €, Paco
€, Paco  € y Luis
€ y Luis  €.
€.
Proporcionalidad compuesta
La proporcionalidad compuesta se emplea cuando se relacionan tres o más magnitudes. Entre las magnitudes se pueden establecer relaciones de proporcionalidad directa e inversa, por lo que podemos diferenciar tres casos: proporcionalidad compuesta directa, proporcionalidad compuesta inversa, proporcionalidad compuesta directa-inversa.
Regla de tres compuesta
La regla de tres compuesta se emplea cuando se relacionan tres o más magnitudes,
de modo que a partir de las relaciones establecidas entre las magnitudes conocidas
obtenemos la desconocida.
Como entre las magnitudes se pueden establecer relaciones de proporcionalidad directa
o inversa, podemos distinguir tres casos de regla de tres compuesta. Podemos visitar este artículo para ver a detalle estos casos junto con varios ejemplos.
Interés
Se llama interés al beneficio que produce el dinero prestado. Ese beneficio es directamente proporcional a la cantidad prestada y al tiempo que dura el préstamo.
| Concepto | Nombre | Símbolo |
|---|---|---|
| Cantidad prestada | Capital |  |
| Tiempo del préstamo | Tiempo | 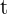 |
| Un beneficio por 100 € en un año | Rédito | 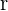 |
| Beneficio del préstamo | Interés | 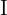 |

Si el tiempo viene expresado en meses:
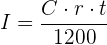
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en la numero dos, el desarrollo, junto con la respuesta esta mal, ya que no se esta contemplando el factor tiempo, que claramente se ve al principio de la formula
Hola si te refieres al problema de pintar una casa, entendemos que no parezca clara esta técnica, también se puede platear de la siguiente forma, por 25 horas de trabajo se paga 500 euros, y resolver el problema en dos casos, cuanto equivale 10 horas y después 15 horas en euros, obteniendo los mismos resultados.
Cuánto se debe depositar cada fin de semestre si usted quiere acumular Bs 10000 al cabo de 4 años conociendo que la entidad financiera reconoce un interés del 12% anual
La numero 7 la respuesta sare de verded y la el numero es que sale de rojo
Hola, si tienes razón y vamos a trabajar en ello, te agradecemos.
esta mal la mayoria de ejercicios la cual se confunde en el mismo ejercicios ep e ip
Hola puedes hacernos el favor de mencionar los ejercicios que están mal para poder corregirlos y así evitar confusiones.
Hola tu razonamiento es correcto si a mayor tamaño de la rueda, mas vueltas da, pero no es así, pues las ruedas grandes dan menos vueltas que las ruedas pequeñas, por eso se usa razones inversamente proporcionales.