Una proporción es una igualdad entre dos razones.
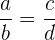
Los/las mejores profesores/as de Matemáticas que están disponibles
Amin
15€
/h
¡1a clase gratis!
Francisco javier
17€
/h
¡1a clase gratis!
Agustina
25€
/h
¡1a clase gratis!
Jose
18€
/h
¡1a clase gratis!
Antonio c
14€
/h
¡1a clase gratis!
Pedro
15€
/h
¡1a clase gratis!
Santiago
18€
/h
¡1a clase gratis!
Viviana
25€
/h
¡1a clase gratis!
Amin
15€
/h
¡1a clase gratis!
Francisco javier
17€
/h
¡1a clase gratis!
Agustina
25€
/h
¡1a clase gratis!
Jose
18€
/h
¡1a clase gratis!
Antonio c
14€
/h
¡1a clase gratis!
Pedro
15€
/h
¡1a clase gratis!
Santiago
18€
/h
¡1a clase gratis!
Viviana
25€
/h
¡1a clase gratis!
Constante de proporcionalidad
Propiedades de las proporciones
1 En una proporción el producto de los medios es igual al producto de los extremos.
Ejemplo:
2En una proporción o en una serie de razones iguales, la suma de los antecedentes dividida entre la suma de los consecuentes es igual a una cualquiera de las razones.
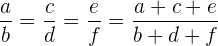
Ejemplo:
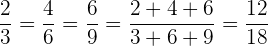
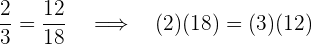
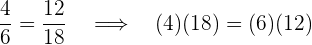
3Si en una proporción cambian entre sí los medios o extremos la proporción no varía.
Ejemplo:
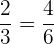
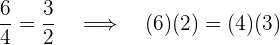
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en la numero dos, el desarrollo, junto con la respuesta esta mal, ya que no se esta contemplando el factor tiempo, que claramente se ve al principio de la formula
Hola si te refieres al problema de pintar una casa, entendemos que no parezca clara esta técnica, también se puede platear de la siguiente forma, por 25 horas de trabajo se paga 500 euros, y resolver el problema en dos casos, cuanto equivale 10 horas y después 15 horas en euros, obteniendo los mismos resultados.
Cuánto se debe depositar cada fin de semestre si usted quiere acumular Bs 10000 al cabo de 4 años conociendo que la entidad financiera reconoce un interés del 12% anual
La numero 7 la respuesta sare de verded y la el numero es que sale de rojo
Hola, si tienes razón y vamos a trabajar en ello, te agradecemos.
esta mal la mayoria de ejercicios la cual se confunde en el mismo ejercicios ep e ip
Hola puedes hacernos el favor de mencionar los ejercicios que están mal para poder corregirlos y así evitar confusiones.
Hola tu razonamiento es correcto si a mayor tamaño de la rueda, mas vueltas da, pero no es así, pues las ruedas grandes dan menos vueltas que las ruedas pequeñas, por eso se usa razones inversamente proporcionales.