¡Bienvenidos a nuestra página dedicada a ejercicios y problemas resueltos con la regla de tres! La regla de tres es una de las herramientas más prácticas y útiles en matemáticas para encontrar proporciones entre distintos objetos. La regla de tres es como una brújula que nos guía a través de situaciones en las que necesitamos relacionar cantidades y encontrar proporciones precisas.
En este espacio, desglosaremos diversos ejercicios y problemas para que puedas perfeccionar tus habilidades en el arte de la proporción. Ya sea que estés buscando mejorar tus capacidades matemáticas cotidianas o necesites aplicar la regla de tres en contextos más complejos, estás en el lugar correcto. ¡Prepárate para desafiar tu mente y convertirte en un experto en la regla de tres!
Si buscas un profesor mates, ¿por qué no encontrarlo en Superprof? ¡La primera clase es gratis!
Dos ruedas están unidas por una correa transmisora. La primera tiene un radio de 
cm y la segunda de 
cm. Cuando la primera ha dado 
vueltas, ¿cuántas vueltas habrá dado la segunda?
Primero notemos que, estas son magnitudes inversamente proporcionales, ya que a más radio dará menos vueltas. Si 
representa el valor de vueltas buscado, del siguiente diagrama obtenemos que
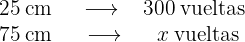
La porción de vueltas es igual a la porción de radio en el siguiente sentido
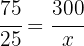
Por lo tanto el valor de es
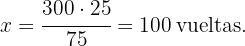
La escala en un mapa es la siguiente: 
cm en el mapa representan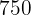 
m en la realidad. ¿A cuánto metros en la realidad equivalen 
cm en el mapa?
Primero notemos que estas son magnitudes son directamente proporcionales, esto es, a más centímetros en el mapa, más metros en la vida real serán. Así, si 
representa el número de metros en la realidad, entonces del siguiente diagrama obtenemos que
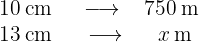
La proporción de metros es igual a la proporción de centímetros en el siguiente sentido
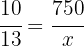
Por lo tanto el valor de es
Seis personas pueden vivir en un hotel durante 
días por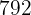 
€. ¿Cuánto costará el hotel de 
personas durante ocho días?
A más personas mayor costo y más días mayor costo también, por tanto son magnitudes directamente proporcionales. Sea el valor de costo que estamos buscando, entonces
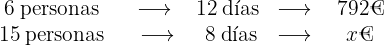
Por lo tanto la porción de personas multiplicada por la porción de días es igual a la porción de dinero, esto es,
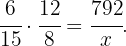
Ahora despejamos el valor de
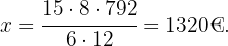
De esta forma el hotel para personas por ocho días costará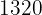 
€.
Una tienda de conveniencia cobra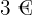 
por cada 
enviados, y si la cantidad no es exacta, se cobra la cantidad correspondiente. Si una persona depositó 
, ¿cuánto le cobró la tienda de conveniencia por el envío?
Primero notemos que estas son magnitudes directamente proporcionales, ya que a más dinero enviado más es el cobro. Así, si representa el monto cobrado por enviar el dinero, del siguiente diagrama obtenemos que
La proporción de dinero cobrado es igual a la proporción de dinero enviado en el siguiente sentido
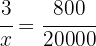
Por lo tanto el valor de es
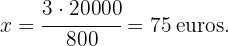
Si con botes de 
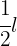de pintura cada uno se han pintado 
m de verja de 
cm de altura. Calcular cuántos botes de 
de pintura serán necesarios para pintar una verja similar de 
cm de altura y 
metros de longitud.
Cuanta más pintura tenga un bote menos botes necesitaremos. Son magnitudes inversamente proporcionales.Cuanta más superficie tengamos que pintar más botes necesitaremos. Son magnitudes directamente proporcionales.Esta información nos permite plantear el siguiente diagrama
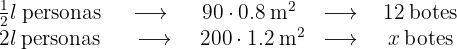
En este caso tenemos que representa el número de botes de pintura que necesitamos. En la columna de la mitad del digrama hemos pasado a la longitud de la verja a metros y hemos calculado el área de dicha verja multiplicando la altura por la longitud.
Ahora despejamos el valor de de la siguiente ecuación
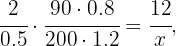
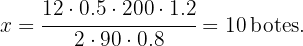
Si una casa tarda en construirse 
días trabajando 
obreros. ¿Cuántos días tardará si se contratan 
obreros adicionales?
Primero notemos que, la variable obreros es inversa a la variable días, ya que, es razonable que, a más obreros trabajando menos tiempo tardarán contruyendo la casa. Así, si representa el valor de días buscado, del siguiente diagrama obtenemos que
La proporción de obreros es inversa a la cantidad de días en el siguiente sentido
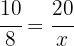
Por lo tanto el valor de es
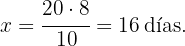
obreros labran un campo rectangular de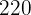 
m de largo y 
de ancho en 
días. ¿Cuántos obreros serán necesarios para labrar otro campo análogo de m de largo por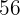 
m de ancho en cinco días?
A más superficie más días necesitaremos. Son magnitudes directamente proporcionales. A más días menos obreros necesitaremos. Son magnitudes inversamente proporcionales. Así tenemos el siguiente diagrama
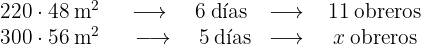
En el planteamiento de diagrama en la primera columna hemos calculado el área del campo, multiplicando el ancho por el largo. Ahora debemos despejar el valor de de la siguiente ecuación
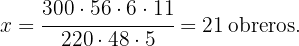
Esto significa que necesitamos para 
obreros para labrar el campo de m de largo por 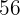m de ancho en cinco días.
Se requieren enfermeras para atender a pacientes en 
días. ¿Cuántas enfermeras se necesitan para atender a 
pacientes en días?
Primero notemos que, a más enfermeras menos son los días que se taradarán en atender a los pacientes, por lo que la variable días es inversa. De la misma manera, a más pacientes, más será la cantidad de enfermeras requeridas por lo que la variable pacientes es directa.Por lo tanto, sea el número de enfermeras que estamos buscando, entonces el problema lo podemos representar de la siguiente manera:
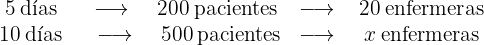
Por lo tanto, la proporción inversa de los días multiplicada por la proporción de pacientes es igual a la proporción de enfermeras ya que la variable días es inversa y la variable pacientes es directa, esto es,
Ahora despejamos el valor de
Seis grifos, tardan horas en llenar un depósito de 
de capacidad. ¿Cuántas horas tardarán cuatro grifos en llenar depósitos de 
cada uno?
A más grifos menos horas. Son magnitudes inversamente proporcionalesA más depósitos más horas. Son magnitudes directamente proporcionalesA más 
más horas. Son magnitudes directamente proporcionalesCon esta información podemos plantear el siguiente diagrama
Estas 
cantidades en proporción se relacionan de la siguiente manera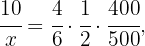
despejando el valor de horas tenemos que
Concluimos que cuatro grifos tardan 
horas en llenar depósitos de .
máquinas de costura hiceron 
prendas el día de ayer. Si el día de hoy solo estarán disponibles 
máquinas, ¿cuántas prendas harán el día de hoy?
Notemos que, la variable máquinas es una variable directa, es decir, al tener menos máquinas se harán menos prendas. Así, si representa el número de prendas buscado, del siguiente diagrama obtenemos que
Por lo tanto, la proporción de máquinas es igual a la proporción de prendas en el siguiente sentido
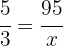
Por lo tanto el valor de 
es
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cuánto se debe depositar cada fin de semestre si usted quiere acumular Bs 10000 al cabo de 4 años conociendo que la entidad financiera reconoce un interés del 12% anual
esta mal la mayoria de ejercicios la cual se confunde en el mismo ejercicios ep e ip
Hola puedes hacernos el favor de mencionar los ejercicios que están mal para poder corregirlos y así evitar confusiones.
Buenos días, el ejercicio 1 está mal si la relación fuera directa entre las variables que no lo e como muestra ahí daría 400kg. La respuesta para mí es que: la relación de las variables es indirecta lo que no sé cómo llega a los 25000. No llego a ese número.
La empresa A1 tal pone en la bolsa de valores $134 acciones por 130 c/u para mantenerlas 3 años
La empresa A2 las compra y las pone nuevamente en la bolsa de valores a un interes simple de 30% por los 3 años
La tercera empresa compra estas acciones por 5 años
Durante el primer semestre la empresa A2 ve que las acciones compradas bajan a $100 podría resolverlo con las cuentas