Resuelve los siguientes problemas:
1Se quiere repartir un premio de 
€ a los tres mejores corredores de una carrera, de manera inversamente proporcional a los tiempos que han invertido en completar el recorrido. El primer corredor tardó 
segundos, el segundo 
y el tercero 
.
El premio del primer corredor es de €
Este campo es obligatorio.
El premio del segundo corredor es de €
Este campo es obligatorio.
El premio del tercer corredor es de €
Este campo es obligatorio.
1Se trata de un reparto inversamente proporcional, porque a más tiempo invertido en acabar el recorrido menos dinero recibirá el corredor. Tomamos los inversos:
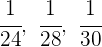
2Pasamos a común denominador:
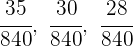
3Ahora realizamos un reparto directamente proporcional a los numeradores:
Obtenemos las siguientes igualdades de las cuales depejamos los valores solicitados
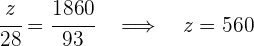
4Así tendríamos que:
El premio del primer corredor es de: 
€
El premio del segundo corredor es de: 
€
El premio del tercer corredor es de: 
€
2Se decide construir una estación de ferrocarril en la comarca del Guadalhorce. El coste es de un millón setescientos mil euros y se acuerda que lo deben pagar las tres localidades principales de manera inversamente proporcional a la distancia a la que se encuentran de la estación. Coín se encuentra a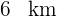 
, Alhaurín el Grande a 
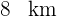y Alhaurín de la Torre a 
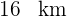de la estación.
a
Sin hacer ningún cálculo, ¿sabrías decir que pueblo deberá aportar una mayor cantidad de dinero?
.
Este campo es obligatorio.
b ¿Cuál será el importe a pagar de cada localidad?
Coín: €
Este campo es obligatorio.
Alhaurín el Grande: €
Este campo es obligatorio.
3Tres amigos ganan un premio de 
€. El premio se reparte de manera inversamente proporcional al número de horas de descanso de cada uno de los miembros. Si el primer miembrp descansó 
horas, el segundo 
y el tercero 
. ¿Qué cantidad recibe cada miembro?
Alhaurín de la Torre: €
Este campo es obligatorio.
1Por ser un reparto inversamente proporcional, el pueblo que deberá aportar más dinero será el que esté a menor distancia de la estación, es decir, Coín.
2Tomamos los inversos:
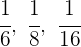
2Pasamos a común denominador:
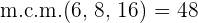
3Ahora realizamos un reparto directamente proporcional a los numeradores:
Obtenemos las siguientes igualdades de las cuales depejamos los valores solicitados
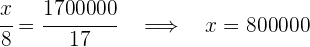
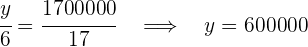
4Así tendríamos que:
Coín debe aportar: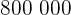 
€
Alhaurín el Grande debe aportar: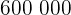 
€
Alhaurín de la Torre debe aportar: 
€
El premio del primer miembro es de €
Este campo es obligatorio.
El premio del segundo miembro es de €
Este campo es obligatorio.
El premio del tercer miembro es de €
Este campo es obligatorio.
1Se trata de un reparto inversamente proporcional, porque a más tiempo de descanso menos dinero recibirá el miembro. Tomamos los inversos:
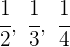
2Pasamos a común denominador:
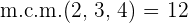
3Ahora realizamos un reparto directamente proporcional a los numeradores:
Obtenemos las siguientes igualdades de las cuales depejamos los valores solicitados
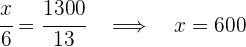
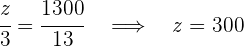
4Así tendríamos que:
El premio del primer corredor es de: €
El premio del segundo corredor es de: 
€
El premio del tercer corredor es de: 
€
4Se reparten 
€ entre tres trabajadores por concepto de pago de manera inversamente proporcional al número de dias no laborados. Si el primer trabajador no laboró 
dias, el segundo y el tercero 
. ¿Cuál es el pago de cada trabajador?
El pago del primer trabajador es de €
Este campo es obligatorio.
El pago del segundo trabajador es de €
Este campo es obligatorio.
El pago del tercer trabajador es de €
Este campo es obligatorio.
1Se trata de un reparto inversamente proporcional, porque a más días no laborados menos dinero recibirá el trabajador. Tomamos los inversos:
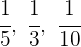
2Pasamos a común denominador:
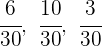
3Ahora realizamos un reparto directamente proporcional a los numeradores:
Obtenemos las siguientes igualdades de las cuales depejamos los valores solicitados
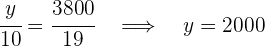
4Así tendríamos que:
El pago al primer trabajador es de: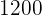 
€
El pago al segundo trabajador es de: 
€
El pago al tercer trabajador es de: €
5Una profesora reparte 
deberes entre tres de sus alumnos de manera inversamente proporcional al número de calificaciones obtenidas. Si el primer alumno tiene una calificación de 
, el segundo 
y el tercero 
. ¿Cuál es el número de deberes asignados a cada alumno?
El primer alumno tendrá deberes.
Este campo es obligatorio.
El segundo alumno tendrá deberes.
Este campo es obligatorio.
El tercer alumno tendrá deberes
Este campo es obligatorio.
1Se trata de un reparto inversamente proporcional, porque a más calificación menos deberes. Tomamos los inversos:
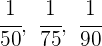
2Pasamos a común denominador:
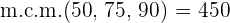
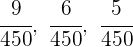
3Ahora realizamos un reparto directamente proporcional a los numeradores:
Obtenemos las siguientes igualdades de las cuales depejamos los valores solicitados
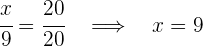
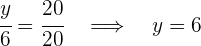
4Así tendríamos que:
El primer alumno tendrá 
deberes
El segundo alumno tendrá 
deberes
El tercer alumno tendrá deberes
6Se reparten 
dulces entre tres niños de manera inversamente proporcional a la edad de cada uno de ellos. Si el primer niño tiene años, el segundo y el tercero . ¿Cuál es el número de dulces que obtiene cada niño?
El niño de 5 años tendrá dulces.
Este campo es obligatorio.
El niño de 6 años tendrá dulces.
Este campo es obligatorio.
El niño de 10 años tendrá dulces.
Este campo es obligatorio.
1Se trata de un reparto inversamente proporcional, porque a más edad menos dulces. Tomamos los inversos:
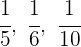
2Pasamos a común denominador:
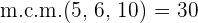
3Ahora realizamos un reparto directamente proporcional a los numeradores:
Obtenemos las siguientes igualdades de las cuales depejamos los valores solicitados
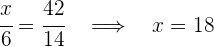
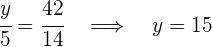
4Así tendríamos que:
El niño de 5 años tendrá 
dulces
El niño de 6 años tendrá 
dulces
El niño de 10 años tendrá dulces
7En un equipo de tres integrantes se reparte un bono de productividad de 
€ de manera inversamente proporcional a la cantidad errores cometidos durante todo el año anterior. Si el primer integrante tiene errores, el segundo y el tercero 
. ¿Cuál es la cantidad que corresponde a cada integrante?
El primer integrante tendrá €.
Este campo es obligatorio.
El segundo integrante tendrá €.
Este campo es obligatorio.
El tercer integrante tendrá €.
Este campo es obligatorio.
1Se trata de un reparto inversamente proporcional, porque a más errores menos bono. Tomamos los inversos:
2Pasamos a común denominador:
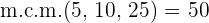
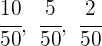
3Ahora realizamos un reparto directamente proporcional a los numeradores:
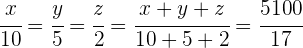
Obtenemos las siguientes igualdades de las cuales depejamos los valores solicitados
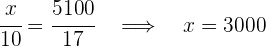
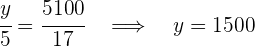
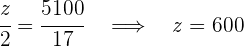
4Así tendríamos que:
El primer integrante tendrá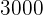 
€
El segundo integrante tendrá 
€
El tercer integrante tendrá €
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cuánto se debe depositar cada fin de semestre si usted quiere acumular Bs 10000 al cabo de 4 años conociendo que la entidad financiera reconoce un interés del 12% anual
esta mal la mayoria de ejercicios la cual se confunde en el mismo ejercicios ep e ip
Hola puedes hacernos el favor de mencionar los ejercicios que están mal para poder corregirlos y así evitar confusiones.
Buenos días, el ejercicio 1 está mal si la relación fuera directa entre las variables que no lo e como muestra ahí daría 400kg. La respuesta para mí es que: la relación de las variables es indirecta lo que no sé cómo llega a los 25000. No llego a ese número.
La empresa A1 tal pone en la bolsa de valores $134 acciones por 130 c/u para mantenerlas 3 años
La empresa A2 las compra y las pone nuevamente en la bolsa de valores a un interes simple de 30% por los 3 años
La tercera empresa compra estas acciones por 5 años
Durante el primer semestre la empresa A2 ve que las acciones compradas bajan a $100 podría resolverlo con las cuentas
Hola tu razonamiento es correcto si a mayor tamaño de la rueda, mas vueltas da, pero no es así, pues las ruedas grandes dan menos vueltas que las ruedas pequeñas, por eso se usa razones inversamente proporcionales.