En esta artículo se presentan ejercicios resueltos de radicales, abarcando desde los conceptos más básicos hasta situaciones más complejas. Cada ejercicio incluye una solución detallada con explicaciones claras, permitiendo reforzar el proceso de análisis, simplificación y manipulación de expresiones radicales.
Representa en la recta: 
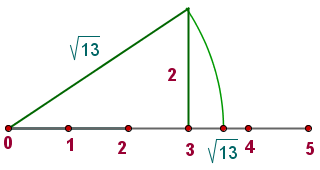
1Tomamos un rectángulo de base 3 y lado 2. Entonces, usando el teorema de Pitágoras encontramos que su diagonal mide
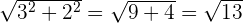
2Basta coger esta medida y transportarla con el compás (tomando centro en 0 y con radio la diagonal de nuestro rectángulo). De este modo, representamos en la recta real el número .
Representa en la recta real los números que verifican las siguientes relaciones:
a
c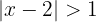
d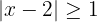
aRepresentamos como desigualdad 
, lo cual en la recta real se representa como
bRepresentamos como desigualdad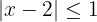 
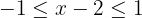
Sumamos 2 en cada término de la desigualdad y obtenemos
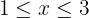
Representamos como intervalo y obtenemos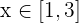 
, lo cual en la recta real se representa como
cRepresentamos como desigualdad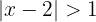 
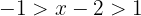
Sumamos 2 en cada término de la desigualdad y obtenemos
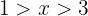
Representamos como intervalo y obtenemos 
, lo cual en la recta real se representa como
dRepresentamos como desigualdad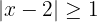 
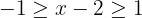
Sumamos 2 en cada término de la desigualdad y obtenemos
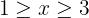
Representamos como intervalo y obtenemos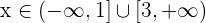 
, lo cual en la recta real se representa como
Opera: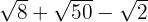 
1Descomponemos en factores los radicandos
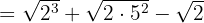
2Extraemos factores,
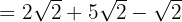
3Como todos los radicales son semejantes podemos sumar sus coeficientes
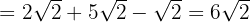
Opera: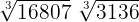 
1Descomponemos en factores los radicandos
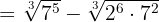
2Extraemos factores,
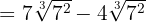
3Como todos los radicales son semejantes podemos sumar sus coeficientes
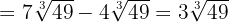
Opera: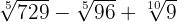 
1Descomponemos en factores los radicandos
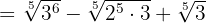
2Extraemos factores,
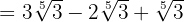
3Como todos los radicales son semejantes podemos sumar sus coeficientes
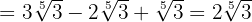
Opera: 
1Descomponemos en factores los radicandos
2En los dos primeros sumandos extraemos factores, el tercero siplificamos el radical dividiendo el índice y el exponente del radicando entre 2 y el último vamos a racionalizar multiplicando y dividiendo por por la raíz cúbica de 2
3Como todos los radicales son semejantes podemos sumar sus coeficientes
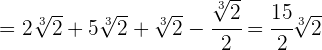
Calcula: 
1En primer lugar calculamos el mínimo común múltiplo de los índices, que será el común índice
2Dividimos el común índice por cada uno de los índices 2, 3, 4 y 6 y cada resultado obtenido se multiplica por sus exponentes correspondientes 1, 2, 3 y 4
3Quitamos los paréntesis, simplificamos la fracción y multiplicamos en el numerador las potencias con la misma base
4Simplificamos el radical dividiendo por 3 el índice y el exponente del radicando
Racionalizar: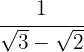 
1Multiplicamos numerador y denominador por el conjugado del denominador
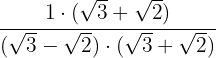
2Desarrollamos el denominador
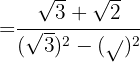
3Realizamos las operaciones
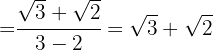
Racionalizar: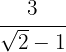 
1Multiplicamos numerador y denominador por el conjugado del denominador
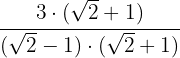
2Desarrollamos el numerados
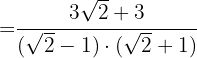
3En el denominador tenemos una suma por diferencia que es igual a la diferencia de cuadrados
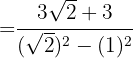
4Realizamos las operaciones
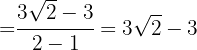
Racionalizar: 
1Multiplicamos numerador y denominador por el conjugado del denominador
2Ponemos el numerador en forma de potencia
3En el numerador tenemos un binomio al cuadrado que es igual al cuadrado del primero, menos el doble del primero por el segundo, más el cuadrado del segundo y en el denominador tenemos una suma por diferencia que es igual a la diferencia de cuadrados
4Realizamos las operaciones
5Simplificamos la fracción
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
hola…como racionalizo 48-6m / la raiz de 4 (dentro de la misma raiz )-raiz de 2m
Hola con gusto te ayudamos, multiplica por la raíz de 4 (dentro de la misma raíz )-raíz de 2m/ la raíz de 4 (dentro de la misma raíz )-raíz de 2m y después por 4 (dentro de la misma raíz )-raíz de 2m/4 (dentro de la misma raíz )-raíz de 2m.
tiene mal la respuesta del 9
Hola revise el ejercicio 9 del artículo y no encontré el error, podrías dar mas detalles por favor para poder corregirlo.
No sé que es disyuntiva, comnutativa
Hola con gusto te ayudamos, con la propiedad disyuntiva significa que si tienes dos opciones y se cumpla una entonces es suficiente por ejemplo «puedes comer en tu casa o en el centro comercial» como puedes ver la propiedad disyuntiva te da opciones, en el caso de la propiedad conmutativa no importa el orden en que hagas una operación puedes sumar «5+4» o «4+5».
Hola analizamos tu observación, si te refieres a (√8+√5)+0=√8+(√5+0) la respuesta es lo que tu comentas «propiedad asociativa de la suma», si me equivoco por favor menciónalo y lo rectificamos con gusto.
El primer ejercicio por que es propiedad distributiva de la suma y no propiedad asociativa de la suma