Los radicales son un concepto fundamental en álgebra, utilizados para expresar raíces de números y variables. Dominar el manejo de radicales es esencial para avanzar en matemáticas, ya que se aplican en una amplia variedad de problemas, desde simplificación de expresiones hasta la resolución de ecuaciones más complejas.
En este conjunto de ejercicios resueltos, exploraremos diferentes tipos de problemas relacionados con radicales. Cada ejercicio está diseñado para reforzar tus conocimientos y habilidades en la manipulación de expresiones radicales, incluyendo la simplificación, la racionalización de denominadores y la potencia radicales.
Calcula los valores de las siguientes potencias racionales:
1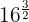
2
3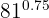
4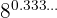
Una potencia con exponente fraccionario es igual a una raíz cuyo índice es el denominador de la fracción y el exponente del radicando es el numerador.
Para resolver, primero descomponemos el radicando en factores, efectuamos las operaciones en el radicando y extraemos factores
1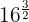
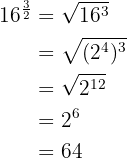
2
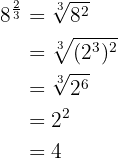
3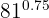
En este caso pasamos el exponente que es un número decimal exacto a fracción
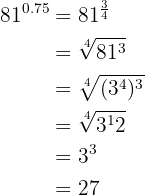
4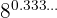
El exponente que es un periódico puro lo pasamos a fracción
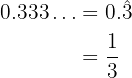
Una vez que conocemos el exponente como fracción, resolvemos
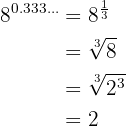
Extraer factores en los siguientes radicales:
1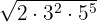
2
1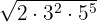
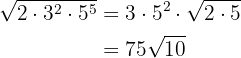
El exponente del dos 
es menor que el índice 
, por tanto se queda en el radicando.
El exponente del 
es igual al índice , por tanto el sale fuera del radicando.
El exponente del 
es mayor que el índice , por tanto se divide dicho.exponente por el índice. El cociente obtenido es el exponente del factor fuera del radicando y el resto es el exponente del factor dentro del radicando.
2
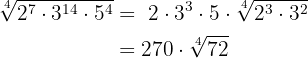
Los exponentes son mayores que el índice, por tanto se dividen dichos
exponentes por el índice.
Cada uno de los cocientes obtenidos será el exponente del factor correspondiente
fuera del radicando y cada uno de los restos obtenidos será el exponente del factor
correspondiente dentro del radicando.
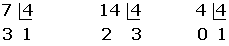
Introducir todos los factores en los radicales:
1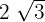 
2
1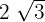
Antes de comenzar a resolver, recordemos algunas propiedades de los radicales. Sabemos que el radical aplicado a un producto es el producto de los radicales
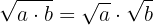
y que el indice del radical cuando se pasa a forma exponencial, divide a la
potencia de la base
entonces estos dos resultados juntos los ocupamos para simplificar a expresiones con radicales multiplicados por factores, es decir
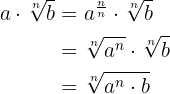
y así podemos solamente ocupar el resultado
Apliquemos ahora este proceso a nuestro problema:
Se introduce el 
elevado al índice del radical y se realizan las operaciones
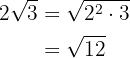
2
Se introducen los factores elevados al índice 
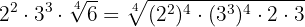
Se realizan las operaciones
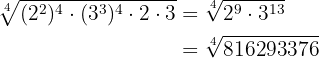
Poner a un índice común los siguientes radicales:
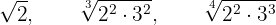
Hallamos el mínimo común múltiplo de los índices, que será el común índice
Dividimos el común índice por cada uno de los índices y cada resultado obtenido se multiplica por sus exponentes correspondientes
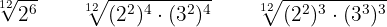
Realizamos las operaciones en los radicales
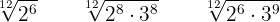
Realiza las sumas de radicales:
1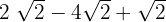
2
3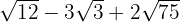
4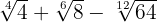
1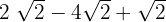
Como los radicales son semejantes sumamos los coeficientes de los radicales:
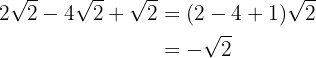
2
Sumamos los coeficientes de los radicales:
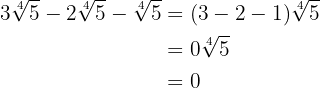
3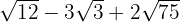
Descomponemos en factores los radicandos y extraemos factores de los radicales (si es posible) y los multiplicamos por el coeficiente del radical correspondiente
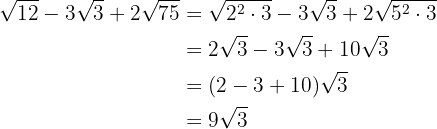
4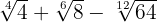
Extraemos factores de los radicales y los multiplicamos por el coeficiente del
radical correspondiente
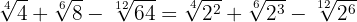
Simplificamos los radicales. En el primer radical dividimos el índice y el exponente del radicando por , en el segundo por y en el tercero por 
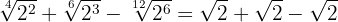
Sumamos los coeficientes de los radicales
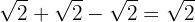
Halla las sumas de radicales convirtiendo al mismo índice:
1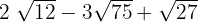
2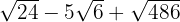
3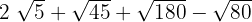
4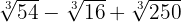
Para realizar estas sumas de radicales no semejantes, seguiremos estos dos pasos:
Descomponemos en factores los radicales y extraemos factores de los radicales (si es posible) y los multiplicamos por el coeficiente del radical correspondiente
Sumamos los coeficientes de los radicales
1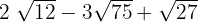
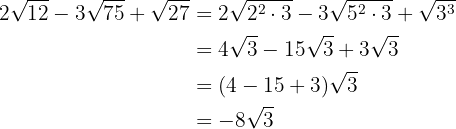
2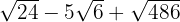
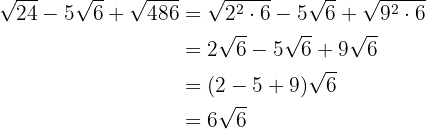
3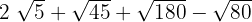
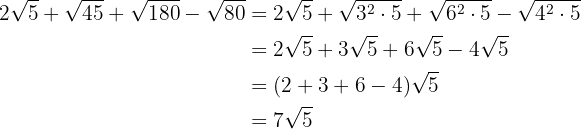
4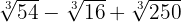
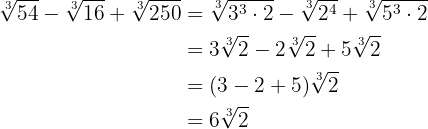
Efectúa las sumas de radicales:
1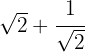
2
1
Racionalizamos el segundo sumando multiplicando y dividiendo por la raíz cuadrada de
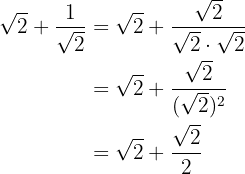
Sacamos factor común de raíz de y sumamos
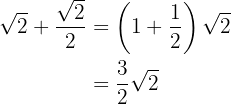
2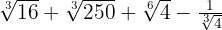 
Descomponemos en factores los radicales
En los dos primeros sumandos extraemos factores, el tercero simplificamos el radical dividiendo el índice y el exponente del radicando entre y el último vamos a racionalizar multiplicando y dividiendo por por la raíz cúbica de
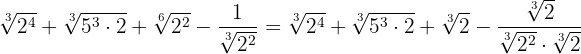
Como todos los radicales son semejantes podemos sumar sus coeficientes
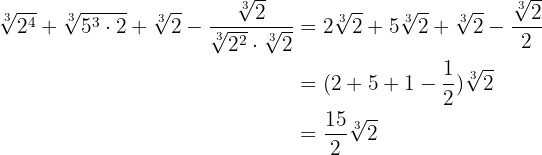
Realizar los productos de radicales:
1
2
3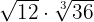
1
Como los radicales tienen el mismo índice multiplicamos los radicandos y
descomponemos en factores para extraer factores del radical.
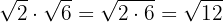
2
Descomponemos en factores los radicandos
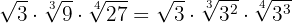
Reducimos a común índice por lo que tenemos que calcular el mínimo común múltiplo de los índices, que será el común índice.
Dividimos el común índice 
por cada uno de los índices 
y cada resultado obtenido se multiplica por sus exponentes correspondientes 
.
Realizamos el producto de potencias con la misma base en el radicando y extraemos factores del radicando
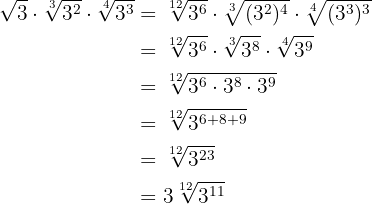
3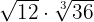
Calculamos el mínimo común múltiplo de los índices.
Procedamos con los cálculos:
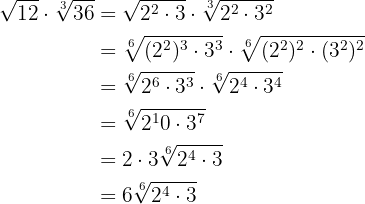
Efectúa las divisiones de radicales:
1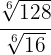
2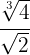
3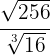
1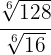
Como los radicales tienen el mismo índice dividimos los radicandos y simplificamos el radical dividiendo el índice y exponente del radicando por
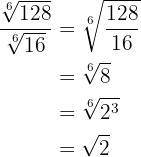
2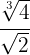
En primer reducimos a común índice por lo que tenemos que calcular el mínimo común múltiplo de los índices, que será el común índice.
.
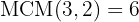Dividimos el común índice 
por cada uno de los índices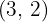 
y cada resultado obtenido se multiplica por sus exponentes correspondientes 
.
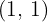Descomponemos el 
en factores para poder hacer la división de potencias con la misma base y dividimos.
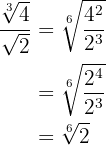
3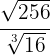
Realizamos los mismos pasos del ejercicio anterior
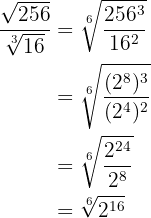
Simplificamos el radical dividiendo por el índice y el exponente del radicando, y
por último extraemos factores
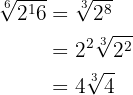
Simplifica la siguiente operación
En primer lugar calculamos el mínimo común múltiplo de los índices, que será elvcomún índice
Dividimos el común índice por cada uno de los índices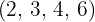 
y cada resultado obtenido se multiplica por sus exponentes correspondientes 
Quitamos los paréntesis, simplificamos la fracción y multiplicamos en el numerador las potencias con la misma base
Simplificamos el radical dividiendo por el índice y el exponente del radicando
Por último extraemos factores
Simplifica a un solo radical
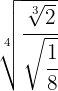
Primero, notemos que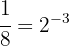 
, por lo tanto
Ponemos a común índice las raíces del numerador y del denominador.
Elevamos al cubo el denominador y realizamos la división de potencias con la misma base.
Realizamos la raíz cuarta del radical multiplicando los índices.
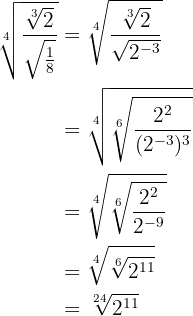
Realiza las operaciones con potencias:
1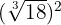
2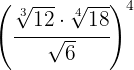
1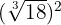
Elevamos el radicando al cuadrado, descomponemos 
en factores y los elevamos al cuadrado y por último extraemos factores
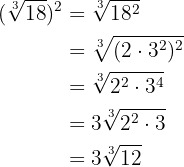
2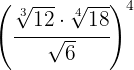
Elevamos los radicandos a la cuarta, descomponemos en factores los radicandos y extraemos el del radical
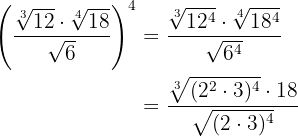
En los radicando realizamos las operaciones con potencias y ponemos a común índice para poder efectuar la división
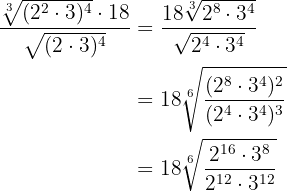
Simplificamos el radical dividiendo por el índice y los exponentes del radicando y realizamos una división de potencias con el mismo exponente
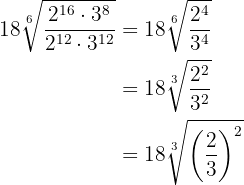
Podemos racionalizar multiplicando y dividiendo por la raíz cúbica de
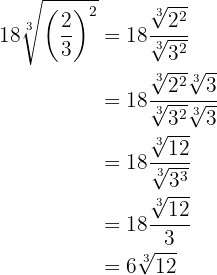
Realiza las operaciones de binomios con radicales:
1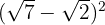
2
3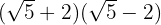
4
1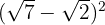
Una diferencia al cuadrado es igual al cuadrado del primero, menos el doble del primero por el segundo, más el cuadrado del segundo
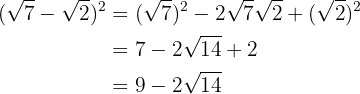
2
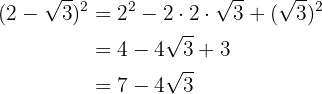
3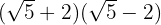
Una suma por diferencia es igual a diferencia de cuadrados
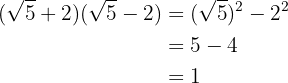
4
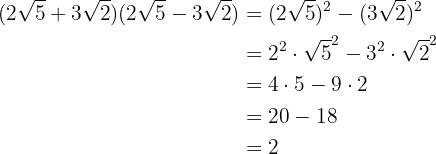
Realiza las siguientes operaciones mixtas con radicales:
1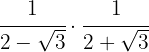
2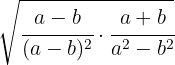
1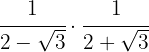
Realizamos la multiplicación de fracciones, en el denominador tenemos una suma por diferencia que es igual a diferencia de cuadrados
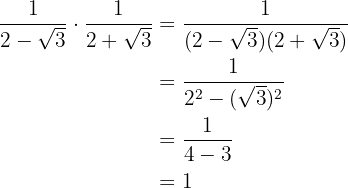
2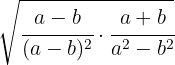
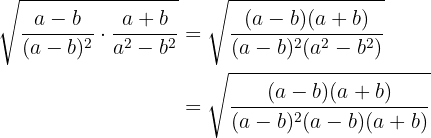
La diferencia de cuadrados del denominador se pone como una suma por diferencia y se simplifica la fracción
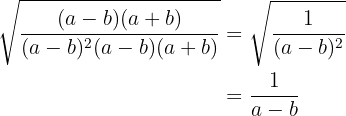
Efectuar las siguientes operaciones de raíces de raíces:
1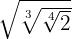
2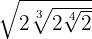
3
1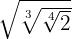
Multiplicamos los índices
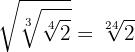
2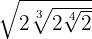
Introducimos el primer dentro de la raíz cúbica por lo que tendremos que elevarlo al cubo y multiplicamos las potencias con la misma base, el procedimiento lo seguimos haciendo hasta que ya se hayan introducido todos los valores en los radicales, y con esto, multiplicamos 
y entonces queda 
.
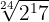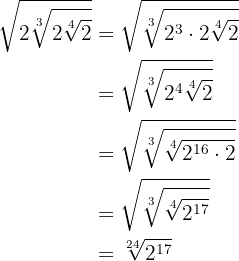
3
Introducimos el dentro de la raíz cuadrada elevándolo al cuadrado.
Multiplicamos las potencias con la misma base.
Multiplicamos los índices y simplificamos dividiendo por 3 el índice resultante y el exponente del radicando.
Racionalizar los radicales:
1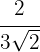
2
3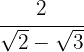
4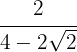
5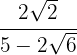
1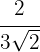
Multiplicamos numerador y denominador por la raíz de , realizamos los cálculos y simplificamos la fracción.
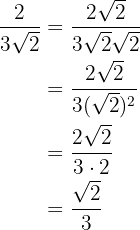
2
El radicando lo ponemos en forma de potencia: 
.
Tenemos que multiplicar en el numerador y denominador por la raíz quinta de 
.
Multiplicamos los radicales del denominador, extraemos factores del radical y simplificamos la fracción.
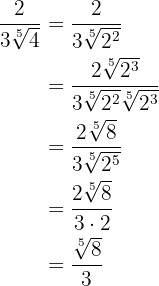
3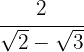
Multiplicamos numerador y denominador por el conjugado del denominador, quitamos paréntesis en el numerador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados.
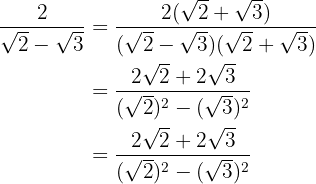
En el denominador extraemos los radicandos y dividimos por 
, es decir, cambiamos el numerador de signo.
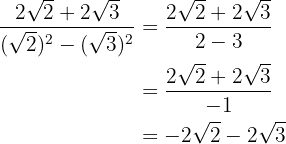
4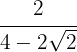
Multiplicamos y dividimos la fracción por el conjugado del denominador.
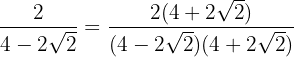
Efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados y operamos:
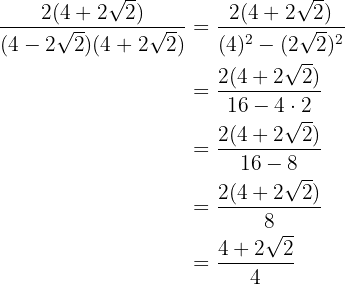
5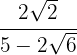
Multiplicamos numerador y denominador por el conjugado del denominador, quitamos paréntesis en el numerador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados.
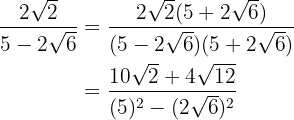
En el numerador descomponemos en factores 
y extraemos factores, terminamos realizando las operaciones del denominador.
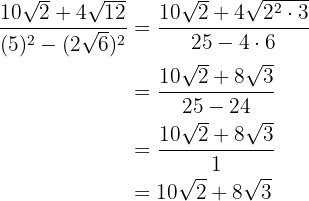
Racionalizar los siguientes radicales:
1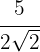
2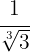
3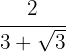
4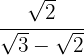
5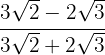
1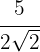
Multiplicamos numerador y denominador por la raíz de y realizamos los cálculos
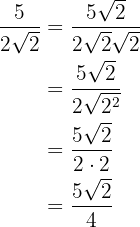
2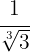
Aquí nos damos cuenta que para poder eliminar el radical de 
necesitamos generar el producto
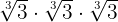
para que de esta forma se elimine el radical, es decir
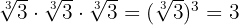
en otras palabras, como ya tenemos a en el denominador, sólo hace falta multiplicarlo por 
para lograr eliminar el radical.
Para no afectar el valor numérico de la expresión, se multiplica tanto en el numerador como en el denominador, y entonces así es como queda nuestro desarrollo
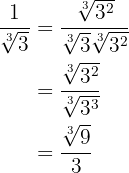
3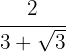
Multiplicamos y dividimos la fracción por el conjugado del denominador.
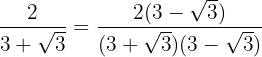
En el numerador quitamos paréntesis y el denominador efectuamos la suma por diferencia, por lo que obtenemos una diferencia de cuadrados.
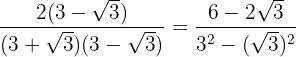
Efectuamos las operaciones y se simplifica la fracción al factorizar el
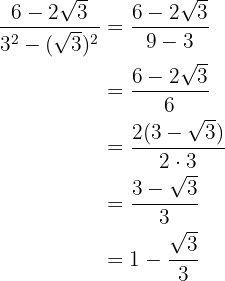
4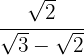
Multiplicamos y dividimos la fracción por el conjugado del denominador
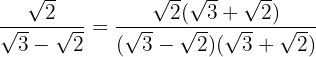
En el numerador quitamos paréntesis y el denominador efectuamos la suma por diferencia, por lo que obtenemos una diferencia de cuadrados
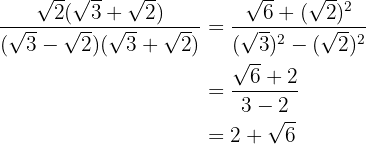
5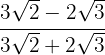
Multiplicamos numerador y denominador por el conjugado del denominador
Ponemos el numerador en forma de potencia
En el numerador tenemos una diferencia al cuadrado que es igual al cuadrado del primero, menos el doble del primero por el segundo, más el cuadrado del segundo. En el denominador tenemos una suma por diferencia que es igual a la diferencia de cuadrados
Realizamos las operaciones y simplificamos al final
¿Necesitas clases de matematicas? En Superprof te damos muchas opciones para que tú elijas la que mejor te venga, desde un profesor de matematicas online hasta clases a domicilio.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
hola…como racionalizo 48-6m / la raiz de 4 (dentro de la misma raiz )-raiz de 2m
Hola con gusto te ayudamos, multiplica por la raíz de 4 (dentro de la misma raíz )-raíz de 2m/ la raíz de 4 (dentro de la misma raíz )-raíz de 2m y después por 4 (dentro de la misma raíz )-raíz de 2m/4 (dentro de la misma raíz )-raíz de 2m.
tiene mal la respuesta del 9
Hola revise el ejercicio 9 del artículo y no encontré el error, podrías dar mas detalles por favor para poder corregirlo.
Cómo se resuelve 1/4-3/4÷4/5² todo la operación dentro de una raíz cúbica
No sé que es disyuntiva, comnutativa
Hola con gusto te ayudamos, con la propiedad disyuntiva significa que si tienes dos opciones y se cumpla una entonces es suficiente por ejemplo «puedes comer en tu casa o en el centro comercial» como puedes ver la propiedad disyuntiva te da opciones, en el caso de la propiedad conmutativa no importa el orden en que hagas una operación puedes sumar «5+4» o «4+5».
Hola analizamos tu observación, si te refieres a (√8+√5)+0=√8+(√5+0) la respuesta es lo que tu comentas «propiedad asociativa de la suma», si me equivoco por favor menciónalo y lo rectificamos con gusto.