Una multiplicación formada por factores iguales se puede escribir en forma de potencia: 
, donde 
, conocida como la base, es el número que se repite y 
, conocido como el exponente, es el número de veces que se repite el factor. Por ejemplo, tendríamos que
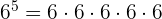
Para este ejemplo de potencia tendríamos que la base es 
, mientras que el exponente es 
.
Potencia con exponente entero positivo
Por notación, cuando en una potencia el exponente es entero positivo, tenemos que
Para determinar el signo de una potencia con exponente entero tendremos en cuenta que:
1 Las potencias con exponente par son siempre positivas. Esto quiere decir que, si tenemos una potencia , entonces:
-
- Si es positivo y es par, entonces es positivo.
- Si
- Si es negativo y es par, entonces es positivo.
Ejemplo:
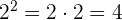
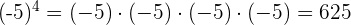
2 Las potencias con exponente impar siempre tienen el mismo signo que su base. Esto quiere decir que, si tenemos una potencia , entonces:
-
- Si es positivo y es impar, entonces es positivo.
- Si
- Si es negativo y es impar, entonces es negativo.
Ejemplo:
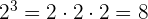
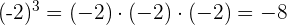
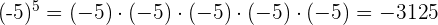
Potencia con exponente entero negativo
Una potencia con exponente negativo es igual al inverso multiplicativo de la base de la potencia elevado al exponente positivo (siempre que la base sea distinta de cero). Así, tenemos que
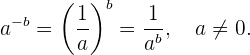
Y para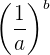 
se cumplen las mismas propiedades mencionadas anteriormente para exponentes positivos.
Ejemplo:
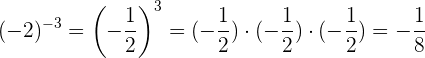
Potencias de números racionales
Potencia de número positivo
Cuando en una potencia la base es fraccionaria, elevamos tanto el numerador como el denominador al exponente.
Ejemplo:
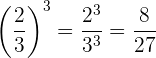
Potencia con base fraccionaria y exponente negativo
Una potencia con base fraccionaria y exponente negativo es igual al inverso multiplicativo de la base elevado al exponente positivo. Recordemos que el inverso de una fracción es igual a cambiar el numerador y el denominador entre sí, esto es, el inverso de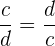 
. Por lo tanto, tenemos que
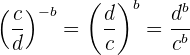
Ejemplo:
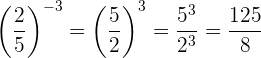
Potencia con exponente racional o fraccionario
Una potencia con exponente fraccionario es igual a una raíz cuyo índice es el denominador de la fracción y el exponente del radicando es el numerador.
Potencia de exponente racional positivo
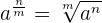
Ejemplos:
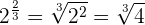
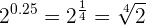
En este caso pasamos el exponente que es un decimal exacto a su fracción equivalente.
Potencia de exponente racional negativo
Al igual que en los casos anteriores, cuando el exponente es fraccionario negativo, es equivalente a elevar el inverso multiplicativo de la base al exponente positivo. Así, tendríamos que
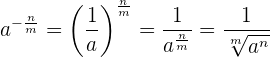
Ejemplo:
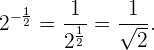
Propiedades de potencias
Un número elevado a 0 es igual a 1.
Por ejemplo: 
.
Un número elevado al exponente 1 es igual a sí mismo.
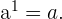
Por ejemplo: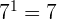 
.
Producto de potencias con la misma base.
Cuando multiplicamos dos potencias con la misma base, el resultado es otra potencia con la misma base elevada a la suma de los exponentes originales.
Ejemplo:
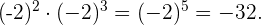
División de potencias con la misma base
Cuando tenemos la división de dos potencias con la misma base, el resultado es otra potencia con la misma base elevada al exponente del numerador menos el exponente del denominador.
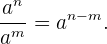
Ejemplo:
.
Potencia de una potencia
Cuando tenemos una potencia de una potencia, el resultado es otra potencia con la misma base elevada al producto de los exponentes.
Ejemplo:
.
.
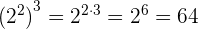Producto de potencias con el mismo exponente
Cuando tenemos la multiplicación de dos potencias con el mismo exponente, el resultado es una nueva potencia en donde la base es la multiplicación de las bases originales elevada al mismo exponente.
Ejemplo:
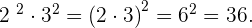
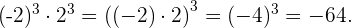
Cociente de potencias con el mismo exponente
Cuando tenemos el cociente de dos potencias con el mismo exponente, el resultado es una nueva potencia en donde la base es el cociente de las bases originales elevada al mismo exponente.
Ejemplo:
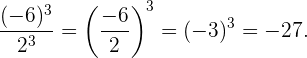
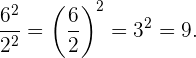
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
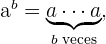
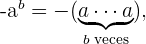
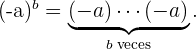
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Que el producto de radicales no necesariamente es un radical
Hola, así es existen casos donde el producto de radicales no es un radical, por ejemplo (√2 )(√32)=√64=8.
¿Cómo puedo citar su contenido? No encuentro el autor y año de actualización de la información y utilizo mucho de su material. Agradecería su respuesta, soy maestra en una institución de educación superior en México
¡Hola! 😊 Nos alegra mucho saber que utilizas nuestro contenido. Para citarlo, puedes hacerlo mencionando Superprof como autor y el enlace del artículo. Por ejemplo:
Superprof. (s.f.). Título del artículo. Disponible en: [URL] 📚
Utilizamos “(s.f.)” cuando no aparece la fecha de publicación. ¡Esperamos que te sea útil! 🙌✨
Nesesito mas ejercicio resueltos
de la racionalizacion
Hola, entendemos tu necesidad esperamos en un cercano futuro tener más artículos con el tema que deseas y poder ayudarte más.
En donde hay operaciones combinadas con numeros reales?
Hola con gusto te recomendamos, ejercicios de números reales 1 y 2, además de ejercicios interactivos del mismo tema.