Elige la opción correcta:
El conjunto de números 
\left\lbrace x\in\mathbb{R}\:|\:|x|<3\right\rbrace[/latex] está formado por todos los números
Selecciona una respuesta.
Debemos analizar la desigualdad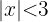 
. Por definición de valor absoluto esta inecuación es igual a 
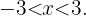Esto nos dice que el conjunto 
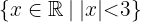es igual a todos los números entre 
y 
sin incluirlos ya que la desigualdad es estricta.
El conjunto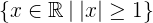 
está formado por todos los números...
Selecciona una respuesta.
Debemos analizar la desigualdad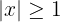 
. Por definición de valor absoluto esta inecuación es igual a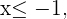 
Esto nos dice que el conjunto 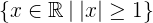es igual a todos los números menores o iguales a 
y mayores o iguales 
.
La expresión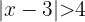 
se reduce a...
Selecciona una respuesta.
Al analizar la desigualdad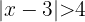 
. Obtenemos por definición de valor absoluto que esta inecuación es igual a 
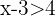y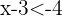 
. Ahora resolvemos estas dos desigualdades sumando en cada lado de las desigualdades,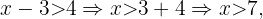 
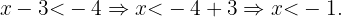Esto nos dice que la desigualdad 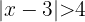se reduce a 
, 
.
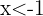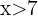La representación de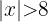 
es...
a
b
c
Selecciona una respuesta.
Al analizar la desigualdad 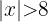. Por definición de valor absoluto esta inecuación es igual a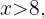 
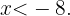Esto nos dice que los valores que satisfacen 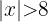son aquellos mayores que ocho y menores que menos ocho sin incluirlos, es decir, la primera figura.
La expresión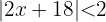 
se representa por...
a
b
c
Selecciona una respuesta.
Por definición de valor absoluto la inecuación 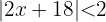se reescribe de la siguiente forma 
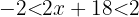Ahora al restar 
en ambos lados y dividiendo por 
se sigue que 
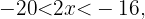
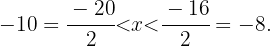Esto nos dice que los valores que satisfacen 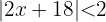son aquellos entre menos diez y menos ocho sin incluirlos, es decir, la segunda figura.
La solución de la expresión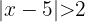 
se puede escribir como...
Selecciona una respuesta.
Por definición de valor absoluto la inecuación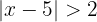 
se reescribe de las siguientes forma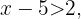 
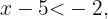Ahora al sumar 
en ambos lados se sigue que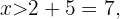 
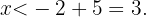Esto nos dice que los valores que satisfacen 
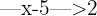son aquellos mayores que siete y los menores que tres sin incluirlos, es decir, la primera figura.
...
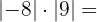Selecciona una respuesta.
Debemos analizar cada uno de los valores que estan dentro de la función valor absoluto. Para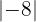 
tenemos que 
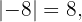pues el número es negativo. En el caso de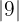 
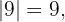pues el número es positivo. Finalmente concluimos que
...
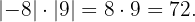
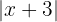Selecciona una respuesta.
Este problema sugiere utilizar la desigualdad del triángulo. La cual nos dice básicamente que el todo es menor que la suma de sus parte, es decir,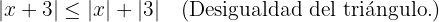 
Dado que no sabemos el signo del valor 
este se queda tal y como esta. Ya que tiene valor positivo, entonces el valor absoluto nos da el mismo valor. Por tanto obtenemos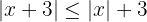 
...
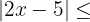Selecciona una respuesta.
Primero agrupamos los signos y valores dentro del valor absoluto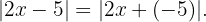 
Ahora aplicamos la desigualdad del triángulo para obtener 
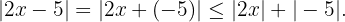Ya que tiene signo negativo entonces su valor absoluto es positivo, así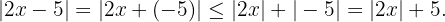 
...
Selecciona una respuesta.
Recordemos que la definición de distancia en los reales es 
Para nuestro caso particular tenemos que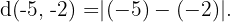 
Desarrollando los parentesis se sigue que 
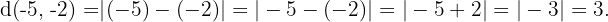Lo que nos dice que la respuesta correcta es
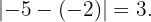
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En donde hay operaciones combinadas con numeros reales?
Hola con gusto te recomendamos, ejercicios de números reales 1 y 2, además de ejercicios interactivos del mismo tema.
hola…como racionalizo 48-6m / la raiz de 4 (dentro de la misma raiz )-raiz de 2m
Hola con gusto te ayudamos, multiplica por la raíz de 4 (dentro de la misma raíz )-raíz de 2m/ la raíz de 4 (dentro de la misma raíz )-raíz de 2m y después por 4 (dentro de la misma raíz )-raíz de 2m/4 (dentro de la misma raíz )-raíz de 2m.
tiene mal la respuesta del 9
Hola revise el ejercicio 9 del artículo y no encontré el error, podrías dar mas detalles por favor para poder corregirlo.
Cómo se resuelve 1/4-3/4÷4/5² todo la operación dentro de una raíz cúbica
Hola analizamos tu observación, si te refieres a (√8+√5)+0=√8+(√5+0) la respuesta es lo que tu comentas «propiedad asociativa de la suma», si me equivoco por favor menciónalo y lo rectificamos con gusto.