
Propiedades y operaciones con radicales
Un radical es una expresión de la forma 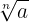 , en la que
, en la que 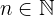 y
y 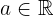 . Además, si
. Además, si 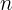 es par, entonces
es par, entonces  no puede ser negativo
no puede ser negativo 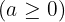 .
.
Por ejemplo, tenemos que  es par. Por lo tanto,
es par. Por lo tanto, 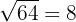 ; mientras que
; mientras que 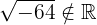 .
.
Asimismo, como  es impar, entonces
es impar, entonces 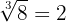 y
y 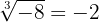 . Es decir, la raíz cúbica está definida para cualquier número real.
. Es decir, la raíz cúbica está definida para cualquier número real.
Las partes que componen un radical son: coeficiente, índice y radicando

Potencias y radicales
Se puede expresar un radical en forma de potencia:
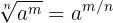
Radicales equivalentes
Utilizando la notación de exponente fraccionario y la propiedad de las fracciones que dice que si se multiplica numerador y denominador por un mismo número la fracción es equivalente, obtenemos que:
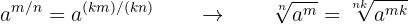
Si se multiplican o dividen el índice y el exponente o exponentes del radicando por un mismo número natural, se obtiene otro radical equivalente.
Simplificación de radicales
Si existe un número natural que divida al índice y al exponente (o los exponentes) del radicando, se obtiene un radical simplificado.
Reducción a índice común
Para reducir a común índice dos a más radicales:
1 Hallamos el mínimo común múltiplo de los índices, que será el común índice
2 Dividimos el común índice por cada uno de los índices y cada resultado obtenido se multiplica por sus exponentes correspondientes
Extracción de factores en un radical
Para extraer factores de un radical se descompone el radicando en factores. Si:
1 Un exponente del radicando es menor que el índice: El factor correspondiente se deja en el radicando.
2Un exponente del radicando es igual al índice: El factor correspondiente sale fuera del radicando.
3Un exponente del radicando es mayor que el índice: Se divide dicho exponente por el índice. El cociente obtenido es el exponente del factor fuera del radicando y el resto es el exponente del factor dentro del radicando.
Introducción de factores en un radical
Para introducir factores en un radical se elevan los factores al índice del radical.
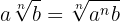
Operaciones con radicales
Para los radicales se tienen las operaciones de suma, resta, multiplicación, divisón y otras que veremos a continuación:
1Suma y resta de radicales
Solamente pueden sumarse (o restarse) dos radicales cuando son radicales semejantes, es decir, si son radicales con el mismo índice e igual radicando.
Para sumar radicales con el mismo índice e igual radicando se se suman los coeficientes de los radicales.

2Multiplicación de radicales.En la multiplicación tenemos dos casos: con el mismo índice o con distinto índice.
aMultiplicación de radicales con el mismo índice. Para multiplicar radicales con el mismo índice se multiplican los radicandos y se deja el mismo índice.

bMultiplicación de radicales con distinto índice. Primero se reducen a común índice y luego se multiplican.
3División de radicales. En la división tenemos dos casos: con el mismo índice o con distinto índice
aDivisión de radicales con el mismo índice. Para dividir radicales con el mismo índice se dividen los radicandos y se deja el mismo índice.
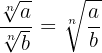
bDivisión de radicales con distinto índice. Primero se reducen a índice común y luego se dividen.
4Potencia de un radical. Para elevar un radical a una potencia, se eleva a dicha potencia el radicando y se deja el mismo índice.
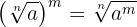
4Racionalización. Consiste en quitar los radicales del denominador, lo que permite facilitar el cálculo de operaciones como la suma de fracciones
Podemos distinguir tres casos:
aRacionalización del tipo 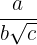
Se multiplica el numerador y el denominador por 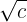

bRacionalización del tipo 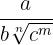
Se multiplica numerador y denominador por 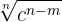
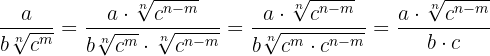
bRacionalización del tipo 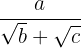 y en general cuando el denominador sea un binomio con al menos un radical.
y en general cuando el denominador sea un binomio con al menos un radical.
Se multiplica el numerador y denominador por el conjugado del denominador.
El conjugado de un binomio es igual al binomio con el signo central cambiado:
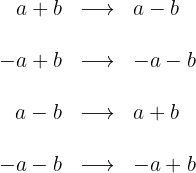
También tenemos que tener en cuenta que: "suma por diferencia es igual a diferencia de cuadrados".
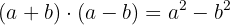
Ejercicios con radicales
Escribir en forma de potencia 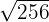
Ponemos en forma de potencia al radicando

El índice del radical  se transforma en el denominador y el exponente del radicando
se transforma en el denominador y el exponente del radicando 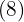 en el numerador y efectuamos las operaciones:
en el numerador y efectuamos las operaciones:
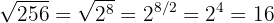
Un radical equivalente de  es
es 
Multiplicamos el índice y el exponente del radicando por un entero positivo, por ejemplo 
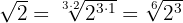
Simplificar:
1 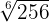
2 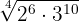
1 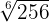
Ponemos en forma de potencia al 

Para simplificar el radical dividimos por  tanto el índice
tanto el índice  como el exponente del radicando
como el exponente del radicando 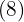
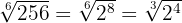
2
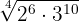
Para simplificar el radical dividimos por  tanto el índice
tanto el índice  como los exponentes del radicando
como los exponentes del radicando 
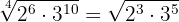
Poner a común índice los radicales: 
En primer lugar hallamos el m.c.m. de los índices: 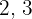 y
y 
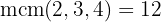
Dividimos el común índice  por cada uno de los índices
por cada uno de los índices 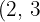 y
y 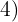 y cada resultado obtenido se multiplica por sus exponentes correspondientes
y cada resultado obtenido se multiplica por sus exponentes correspondientes

Operamos con las potencias

Verificar si es posible extraer los factores de:
1
2 
1
puesto que 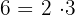 y los exponentes de los factores es 1, el cual es menor que el índice 2; así
y los exponentes de los factores es 1, el cual es menor que el índice 2; así
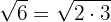
2 
Puesto que 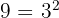 y el exponente 2 es menor que el índice 3; así
y el exponente 2 es menor que el índice 3; así

Extraer los factores de:
1 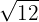
2 
1 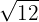
Descomponemos  en factores, como el
en factores, como el  está elevado a la misma potencia que el índice podemos extraer el
está elevado a la misma potencia que el índice podemos extraer el  del radicando; así se obtiene
del radicando; así se obtiene

2 
Descomponemos  en factores, como el
en factores, como el  está elevado a la misma potencia que el índice podemos extraer el
está elevado a la misma potencia que el índice podemos extraer el  del radicando; así se obtiene
del radicando; así se obtiene
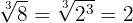
Extraer los factores de:
1 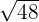
2 
3 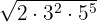
4 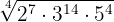
1 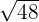
El exponente del 2 es mayor que el índice, por tanto se divide dicho exponente  entre el índice
entre el índice 
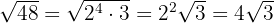
El cociente obtenido  es el exponente del factor fuera del radicando y el resto
es el exponente del factor fuera del radicando y el resto 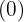 es el exponente del factor dentro del radicando.
es el exponente del factor dentro del radicando.
Como el factor  es igual a 1, no es necesario colocarlo en el radicando ya que si se multiplica por otro factor este no varía
es igual a 1, no es necesario colocarlo en el radicando ya que si se multiplica por otro factor este no varía
En general, si el resultado de dividir el exponente de un factor por el índice da como resto cero, no colocaremos ese factor en el radicando
2 
Descomponemos en factores: 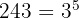
El exponente es mayor que el índice, por tanto se divide dicho exponente  entre el índice
entre el índice 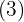 .
.
El cociente obtenido  es el exponente del factor fuera del radicando y el resto
es el exponente del factor fuera del radicando y el resto  es el exponente dentro del radicando
es el exponente dentro del radicando

3 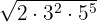
Hay exponentes en el radicando mayores que el índice, por tanto se dividen dichos exponentes 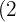 y
y 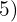 por el índice
por el índice  .
.
Cada uno de los cocientes  y
y  obtenidos será el exponente del factor correspondiente fuera del radicando y cada uno de los restos obtenidos
obtenidos será el exponente del factor correspondiente fuera del radicando y cada uno de los restos obtenidos  y
y  serán los exponentes de los factores correspondientes dentro del radicando
serán los exponentes de los factores correspondientes dentro del radicando

4 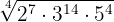
Los exponentes el radicando son mayores que el índice, por tanto se dividen dichos exponentes  y
y 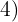 por el índice
por el índice  .
.
Cada uno de los cocientes 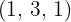 obtenidos será el exponente del factor correspondiente fuera del radicando y cada uno de los restos obtenidos
obtenidos será el exponente del factor correspondiente fuera del radicando y cada uno de los restos obtenidos 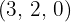 serán los exponentes de los factores correspondientes dentro del radicando
serán los exponentes de los factores correspondientes dentro del radicando

Introducir los factores en el radical:
1 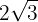
2 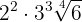
1 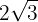
Como el índice es  , el factor fuera del radical
, el factor fuera del radical  se eleva al cuadrado y realizamos las operaciones
se eleva al cuadrado y realizamos las operaciones
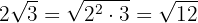
2 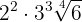
Tanto el  como el
como el  se introducen elevados a la cuarta potencia, es decir,
se introducen elevados a la cuarta potencia, es decir,
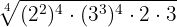
Quitamos los paréntesis multiplicando los exponentes y multiplicamos las potencias con la misma base

Realizar las sumas:
1 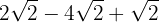
2 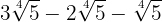
3 
4 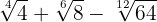
5 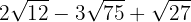
6 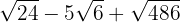
7 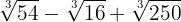
8 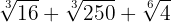
1 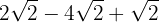
Sumamos y restamos (dependiendo de los signos) los coeficientes de los radicales y tenemos
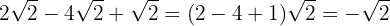
2 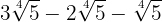
Sumamos los coeficientes de los radicales
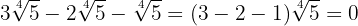
3 
Descomponemos en factores los radicandos:

De manera que las raíces son
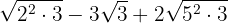
Extraemos factores de los radicales y los multiplicamos por el coeficiente del radical correspondiente
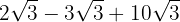
Sumamos los coeficientes de los radicales
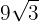
4 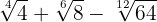
Extraemos factores de los radicales y los multiplicamos por el coeficiente del radical correspondiente
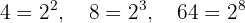
De manera que
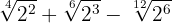
Simplificamos los radicales. En el primer radical dividimos el índice y el exponente del radicando por  , en el segundo por
, en el segundo por  y en el tercero por
y en el tercero por 
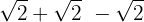
Sumamos los coeficientes de los radicales
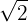
5 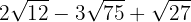
Expresamos los radicandos en factores
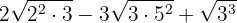
Extraemos factores del radicando
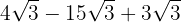
Sumamos los coeficentes y tenemos
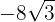
6 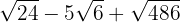
Expresamos los radicandos en factores
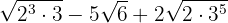
Extraemos factores del radicando
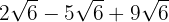
Sumamos los coeficentes y tenemos

7 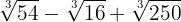
Expresamos los radicandos en factores
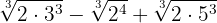
Extraemos factores del radicando
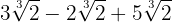
Sumamos los coeficentes y tenemos

8 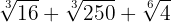
Expresamos los radicandos en factores
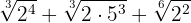
Extraemos factores del radicando
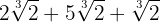
Sumamos los coeficentes y tenemos
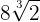
Realizar la multiplicación 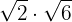
Multiplicamos los radicandos
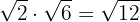
Cuando terminemos de realizar una operación extraeremos factores del radical, si es posible.
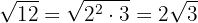
Realizar las multiplicaciones:
1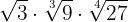
2 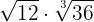
1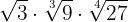
Descomponemos en factores los radicandos

Reducimos a común índice por lo que tenemos que calcular el mínimo común múltiplo de los índices, que será el común índice.
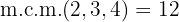
Dividimos el común índice  por cada uno de los índices
por cada uno de los índices 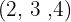 y cada resultado obtenido se multiplica por sus exponentes correspondientes
y cada resultado obtenido se multiplica por sus exponentes correspondientes  . Realizamos el producto de potencias con la misma base en el radicando y extraemos factores del radicando
. Realizamos el producto de potencias con la misma base en el radicando y extraemos factores del radicando

2 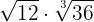
Calculamos el mínimo común múltiplo de los índices

Dividimos el común índice  por cada uno de los índices
por cada uno de los índices 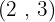 y cada resultado obtenido se eleva a los radicandos correspondientes
y cada resultado obtenido se eleva a los radicandos correspondientes
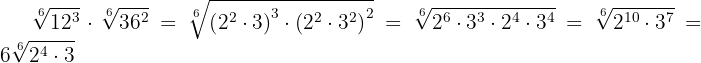
Descomponemos en factores  y
y  , realizamos las operaciones con las potencias y extraemos factores
, realizamos las operaciones con las potencias y extraemos factores
Realizar la división 
Como los dos radicales tienen el mismo índice lo ponemos todo en un radical con el mismo índice
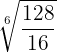
Descomponemos en factores, hacemos la división de potencias con la misma base

Simplificamos el radical dividiendo el índice y el exponente del radicando por 
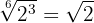
Realiza las divisiones:
1 
2 
3 
1 
En primer reducimos a común índice por lo que tenemos que calcular el mínimo común múltiplo de los índices, que será el común índice  .
.
Dividimos el común índice  por cada uno de los índices (
por cada uno de los índices ( y
y  ) y cada resultado obtenido se multiplica por sus exponentes correspondientes (
) y cada resultado obtenido se multiplica por sus exponentes correspondientes ( y
y  )
)
2

Descomponemos el  en factores para poder hacer la división de potencias con la misma base y dividimos
en factores para poder hacer la división de potencias con la misma base y dividimos
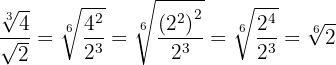
3

Realizamos los mismos pasos del ejemplo anterior

Simplificamos el radical dividiendo por  el índice y el exponente del radicando, y por último extraemos factores
el índice y el exponente del radicando, y por último extraemos factores
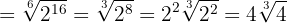
Simplifica:
1 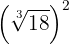
2 
1 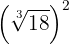
Elevamos el radicando al cuadrado, descomponemos  en factores y los elevamos al cuadrado y por último extraemos factores
en factores y los elevamos al cuadrado y por último extraemos factores
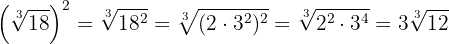
2 
Elevamos los radicandos a la cuarta, descomponemos en factores los radicandos y extraemos el  del radical
del radical
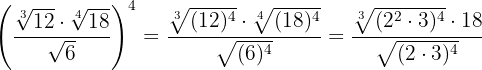
En los radicando realizamos las operaciones con potencias y ponemos a común índice para poder efectuar la división
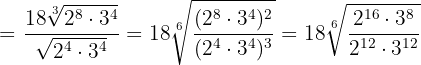
Simplificamos el radical dividiendo por  el índice y los exponentes del radicando y realizamos una división de potencias con el mismo exponente
el índice y los exponentes del radicando y realizamos una división de potencias con el mismo exponente
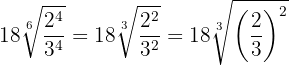
Simplificar:
1 
2 
1 
Multiplicamos los índices
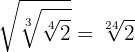
2

Introducimos el primer  dentro de la raíz cúbica por lo que tendremos que elevarlo al cubo y multiplicamos las potencias con la misma base
dentro de la raíz cúbica por lo que tendremos que elevarlo al cubo y multiplicamos las potencias con la misma base
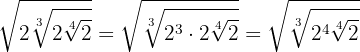
Introducimos el  en la raíz cuarta por lo que tenemos que elevarlo a la cuarta, realizamos el producto de potencias y por último el producto de los índices
en la raíz cuarta por lo que tenemos que elevarlo a la cuarta, realizamos el producto de potencias y por último el producto de los índices

Racionalizar 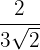
Multiplicamos el numerador y el denominador por 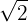
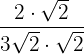
Simplificamos
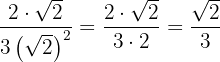
Racionalizar 
El radicando  lo ponemos en forma de potencia:
lo ponemos en forma de potencia: 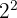
Tenemos que multiplicar en el numerador y denominador por la raíz quinta de 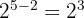
Multiplicamos los radicales del denominador, extraemos factores del radical y simplificamos la fracción

Racionalizar:
1 
2 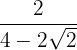
3 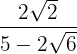
1 
Multiplicamos numerador y denominador por el conjugado del denominador, quitamos paréntesis en el numerador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados
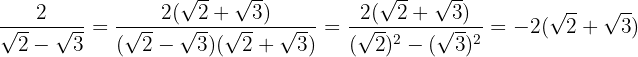
2 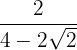
Multiplicamos y dividimos la fracción por el conjugado del denominador
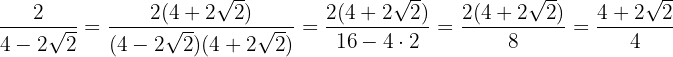
3 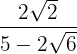
Multiplicamos numerador y denominador por el conjugado del denominador, quitamos paréntesis en el numerador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados
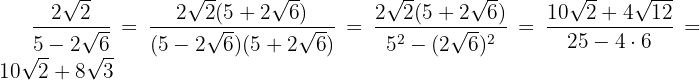
¿Necesitas clases particulares matematicas? No lo dudes y llama a Superprof para pedir más información. En nuestra página podrás encontrar tanto un profesor de matematicas online como uno presencial.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En donde hay operaciones combinadas con numeros reales?
Hola con gusto te recomendamos, ejercicios de números reales 1 y 2, además de ejercicios interactivos del mismo tema.
hola…como racionalizo 48-6m / la raiz de 4 (dentro de la misma raiz )-raiz de 2m
Hola con gusto te ayudamos, multiplica por la raíz de 4 (dentro de la misma raíz )-raíz de 2m/ la raíz de 4 (dentro de la misma raíz )-raíz de 2m y después por 4 (dentro de la misma raíz )-raíz de 2m/4 (dentro de la misma raíz )-raíz de 2m.
tiene mal la respuesta del 9
Hola revise el ejercicio 9 del artículo y no encontré el error, podrías dar mas detalles por favor para poder corregirlo.
Cómo se resuelve 1/4-3/4÷4/5² todo la operación dentro de una raíz cúbica
Hola analizamos tu observación, si te refieres a (√8+√5)+0=√8+(√5+0) la respuesta es lo que tu comentas «propiedad asociativa de la suma», si me equivoco por favor menciónalo y lo rectificamos con gusto.