¡Bienvenido a los ejercicios de números reales! Los números reales son fundamentales en las matemáticas y abarcan una amplia gama de valores, incluyendo los números enteros, fraccionarios, decimales, racionales e irracionales. Estos números se extienden infinitamente en ambas direcciones y son la base para realizar operaciones matemáticas esenciales.
A lo largo de esta serie de ejercicios, pondrás a prueba tus habilidades en diferentes conceptos relacionados con los números reales. Recuerda que los números reales son una herramienta poderosa para representar cantidades y magnitudes en la vida cotidiana y en diversos campos académicos y profesionales. Además, su estudio es esencial para comprender conceptos más avanzados en matemáticas y ciencias.
¡Adelante! Sumérgete en los ejercicios y disfruta reforzando tus habilidades con los números reales.
Clasifica los números:
a 
b 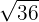
c 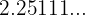
d 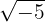
e 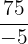
a 
Notemos que  es un número irracional, esto es,
es un número irracional, esto es, 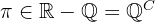 , en donde
, en donde 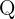 son los números racionales. Se sabe que el producto, división, suma o resta entre un número irracional y uno racional es un número irracional, por lo tanto, tenemos que
son los números racionales. Se sabe que el producto, división, suma o resta entre un número irracional y uno racional es un número irracional, por lo tanto, tenemos que  es irracional
es irracional

b 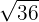
Observemos que podemos resolver esta raíz de manera exacta, esto es, 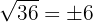 , en donde
, en donde  y
y  son números enteros, por lo tanto
son números enteros, por lo tanto
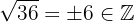
c 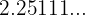
Todo número que tenga decimal periódico se puede expresar como fracción, esto significa que todo número con decimal periódico es un número racional. De hecho, tenemos que, 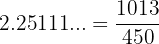 esto comprueba que se trata de un número racional
esto comprueba que se trata de un número racional
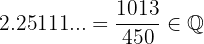
d 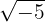
Las raíces de números negativos nunca han pertenecido a los números reales, estos numeros pertenecen a una extensión de los números reales conocido como los números complejos 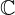 . Dicho lo anterior, este número es un número complejo.
. Dicho lo anterior, este número es un número complejo.
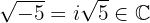
e 
Al tener una fracción entre números enteros es claro que tenemos con número racional, sin embargo, si efectuamos la división, tenemos que esta fracción es equivalente al número entero 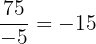 . Dicho lo anterior, tenemos que
. Dicho lo anterior, tenemos que
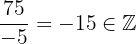
Representa en la recta: 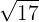
Para encontrarlo, primero notemos que al calcular la raíz, tenemos que
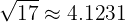
Grafiquemos este punto en la recta

Representa en la recta real los números que verifican las siguientes relaciones:
a 
b 
c 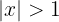
d 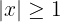
a 
Notemos que por definición de valor absoluto, las siguientes igualdades son equivalentes

En donde la última desigualdad implica que  .
.

b 
Notemos que por definición de valor absoluto, las siguientes igualdades son equivalentes

En donde la última desigualdad implica que  .
.

c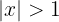
Notemos que por definición de valor absoluto, las siguientes igualdades son equivalentes
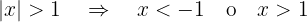 .
.
En donde la última desigualdad implica que  o
o 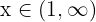 , lo cual lo podemos expresar en términos de la unión de conjuntos como
, lo cual lo podemos expresar en términos de la unión de conjuntos como 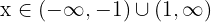 .
.

d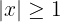
Notemos que por definición de valor absoluto, las siguientes igualdades son equivalentes
 .
.
En donde la última desigualdad implica que  o
o  , lo cual lo podemos expresar en términos de la unión de conjuntos como
, lo cual lo podemos expresar en términos de la unión de conjuntos como  .
.

Calcula los valores de las siguientes potencias:
a
b
c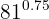
d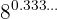
a 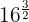
Una potencia con exponente fraccionario es igual a una raíz cuyo índice es el denominador de la fracción  y el exponente del radicando es el numerador
y el exponente del radicando es el numerador 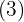 .
.
Descomponemos 16 en factores, efectuamos las operaciones en el radicando y extraemos factores:
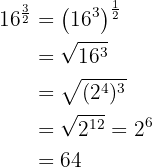
b
Una potencia con exponente fraccionario es igual a una raíz cuyo índice es el denominador de la fracción 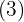 y el exponente del radicando es el numerador
y el exponente del radicando es el numerador  .
.
Descomponemos 8 en factores, efectuamos las operaciones en el radicando y extraemos factores:

c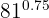
En este caso pasamos el exponente que es un número decimal exacto a fracción:

d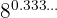
El exponente que es un periódico puro, por lo tanto lo podemos expresar como fracción: 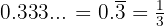 . Por lo tanto
. Por lo tanto
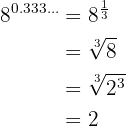
Hallar las sumas:
a
b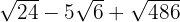
c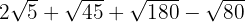
d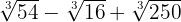
Solucionaremos los ejercicios simplemente descomponiendo el radicando en potencias de números primos. Después con simple álgebra, sumas, y restas, resolveremos los problemas.
a 
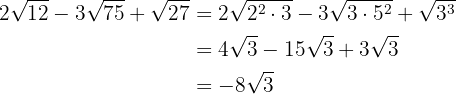
b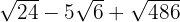
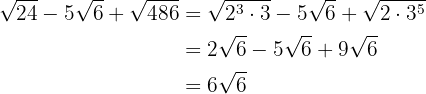
c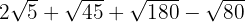
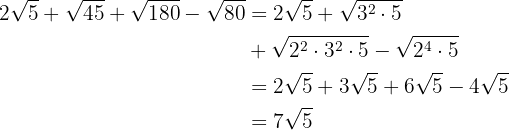
d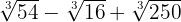
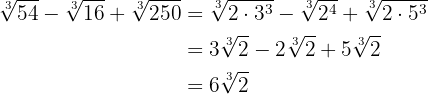
Realiza las operaciones:
a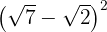
b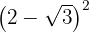
c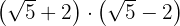
d
Para resolver este ejercicio simplemente aplicaremos la teoría que sabemos sobre potencias y multiplicación de binomios
a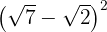
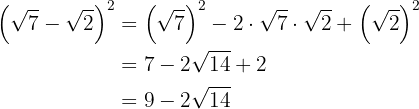
b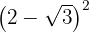
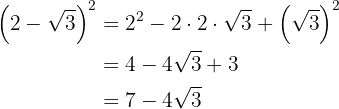
c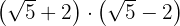
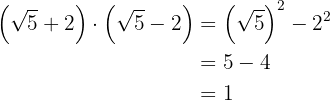
d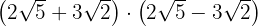
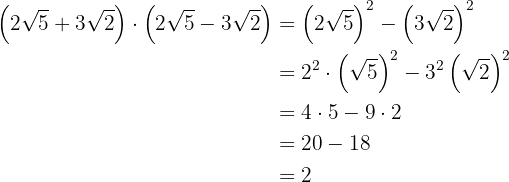
Opera: 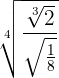
Para resolver este ejercicio aplicaremos gran parte de la teoría de exponentes que conocemos. Jugaremos con las fracciones en los exponentes hasta simplificar de manera adecuada nuestra expresión
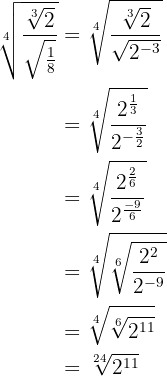
Efectúa: 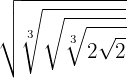
Para resolver este ejercicio aplicaremos equivalencia de potencias fraccionarias con radicales para poder simplificar:
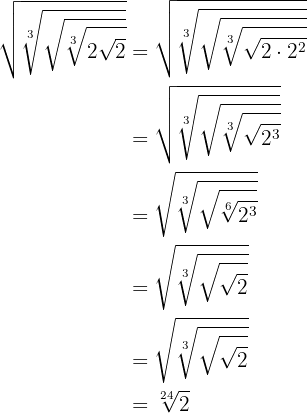
Calcular:
a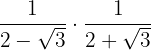
b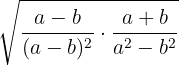
Utilizaremos lo que sabemos de álgebra para realizar estas operaciones:
a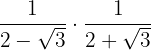
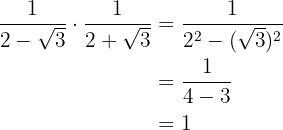
b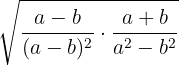
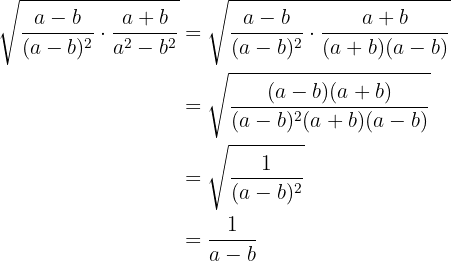
Racionalizar:
a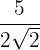
b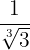
c
d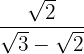
Recordemos que racionalizar consiste en eliminar los radicales del denominador de una fracción, para esto multiplicamos la fracción por un uno multiplicativo adecuado.
a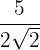
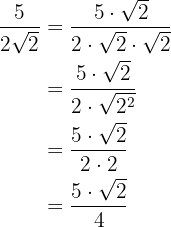
b
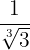
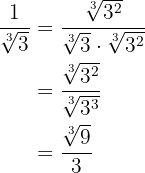
c

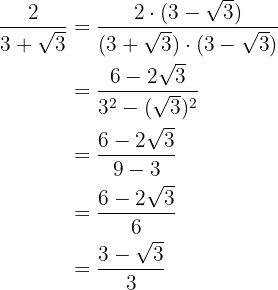
d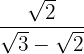
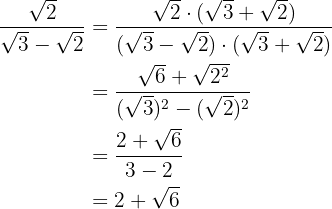
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En donde hay operaciones combinadas con numeros reales?
Hola con gusto te recomendamos, ejercicios de números reales 1 y 2, además de ejercicios interactivos del mismo tema.
hola…como racionalizo 48-6m / la raiz de 4 (dentro de la misma raiz )-raiz de 2m
Hola con gusto te ayudamos, multiplica por la raíz de 4 (dentro de la misma raíz )-raíz de 2m/ la raíz de 4 (dentro de la misma raíz )-raíz de 2m y después por 4 (dentro de la misma raíz )-raíz de 2m/4 (dentro de la misma raíz )-raíz de 2m.
tiene mal la respuesta del 9
Hola revise el ejercicio 9 del artículo y no encontré el error, podrías dar mas detalles por favor para poder corregirlo.
Cómo se resuelve 1/4-3/4÷4/5² todo la operación dentro de una raíz cúbica
Hola analizamos tu observación, si te refieres a (√8+√5)+0=√8+(√5+0) la respuesta es lo que tu comentas «propiedad asociativa de la suma», si me equivoco por favor menciónalo y lo rectificamos con gusto.