Capítulos
Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados.
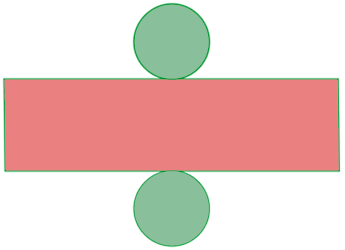
Elementos del cilindro
Un cilindro recto consta de distintas partes que a continuación enunciamos
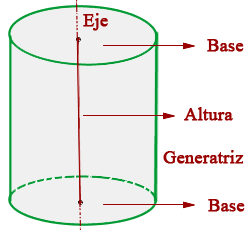
Bases del cilindro
Son los círculos que conforman los bordes inferior y superior el cilindro. Estos círculos son iguales y paralelos.
Eje del cilindro
Es la recta que pasa por los centros de las bases del cilindro; esta es perpendicular a dichas bases. Observa que el eje contiene al lado del rectángulo que gira sobre si mismo.
Altura
Es la longitud del segmento que tiene por extremos los centros de las dos bases. Es igual al lado del rectángulo que gira sobre si mismo.
Generatriz
Es el lado opuesto a la altura y es el lado que engendra el cilindro. Observa que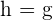 
Área lateral del cilindro
Es igual al área de la superficie del cilindro sin considerar el área de sus bases
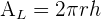
Área del cilindro
Es igual al área total de la superficie del cilindro considerando sus bases
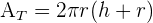
Volumen del cilindro
Ejercicios propuestos
Calcula la cantidad de hojalata que se necesitará para hacer 
botes de forma cilíndrica de 
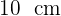de diámetro y 
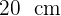de altura.
1La cantidad de hojalata requerida es el área total del cilindro
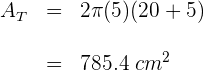
2La cantidad total de hojalata requerida para fabricar botes es
Un cilindro tiene por altura la misma longitud que la circunferencia de la base. Si la altura es de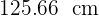 
. Calcular el área total y volumen.
1Primero utilizamos el hecho que la altura es igual a la longitud de la circunferencia de la base para encontrar el valor del radio
2Calculamos el área total
3Calculamos el volumen
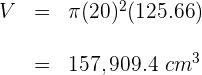
Un cilindro tiene por altura la misma longitud que el radio de su base. Si la altura es de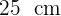 
. Calcular el área lateral.
1Primero utilizamos el hecho que la altura es igual al radio
2Calculamos el área lateral
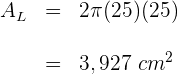
El área lateral de un cilindro es igual a la mitad del área de su base. Si el radio de la base es de 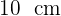. Calcular la altura del cilindro.
1Primero calculamos el área de la base del cilindro
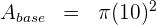
2Igualamos el área lateral con la mitad del área de la base
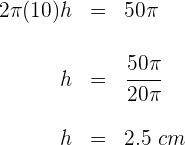
Expresa el área lateral de un cilindro en término de su volumen y su radio.
1A partir de la fórmula de volumen, construimos la fórmula del área lateral
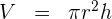
2Multiplicamos ambos lados por 2 y expresamos el radio al cuadrado como un producto de radios
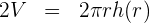
3Despejamos el área lateral
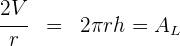
Encuentra el área lateral de un cilindro de radio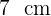 
y volumen 
.
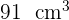1A partir de la fórmula de área lateral de un cilindro en término de su volumen y radio, se obtiene
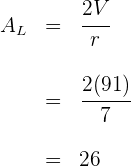
Así, el área lateral es de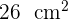 
Encuentra el volumen de un cilindro de radio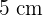 
y área lateral 
.
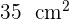1A partir de la fórmula de área lateral de un cilindro en término de su volumen y radio, se obtiene
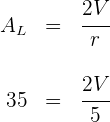
2Despejando el volumen se obtiene
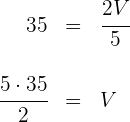
Así, el volumen del cilindro es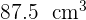 
Encuentra el área total de un cilindro de radio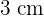 
y área lateral 
.
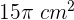1El área total de un cilindro es igual a la suma de su área lateral con el doble del área de su base. Como conocemos el área lateral, solamente nos falta el área de la base.
2Cálculamos el área de la base
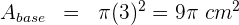
Así, el área total es
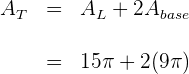
Luego, el área total del cilindro es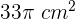 
En una probeta de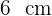 
de radio se echan cuatro cubitos de hielo de 
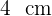de arista. ¿A qué altura llegará el agua cuando se derritan?
1Calculamos el volumen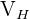 
de un cubito de hielo
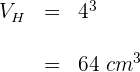
El volumen ocupado por los cuatro cubitos de hielo es 
2Para encontrar la altura de la probeta, igualamos el volumen de la probeta 
con el volumen de agua de los cuatro cubitos
Un recipiente cilíndrico de 10 cm de radio y y 5 cm de altura se llena de agua. Si la masa del recipiente lleno es de 2 kg, ¿cuál es la masa del recipiente vacío?
1Calculamos el volumen del recipiente
2Se sabe que un 
es igual a un 
, por lo que convertimos el volumen a
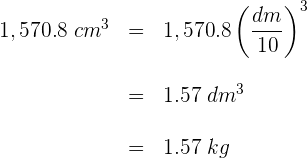
3Así, la masa del recipiente vacio es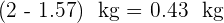 
Si radio de la base de un cilindro se reduce a la mitad, ¿es su volumen igual a la mitad del volumen original?
1Calculamos el volumen del cilindro de radio 
y altura 
2Calculamos el volumen para el cilindro con el radio reducido a la mitad
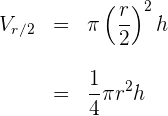
3El volumen del cilindro con el radio reducido a la mitad es igual a una cuarta parte del volumen del cilindro original, y no la mitad de este.
Se desea construir una lata cilíndrica cuyo radio sea la cuarta parte de su altura. Expresa el volumen y el área total de la lata en función del radio de la misma.
1Calculamos el volumen del cilindro de radio y altura
2Utilizamos el hecho de que el radio es igual a un cuarto de la altura, para expresar la altura en término del radio
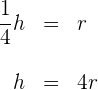
3Sustituimos el valor en la fórmula del volumen, para expresarlo en términos de
4Sustituimos el valor en la fórmula del área total, para expresarlo en términos de
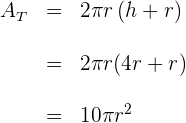
La altura de un cilindro se incrementa 
unidades, ¿cuál es el incremento en su volumen?
1Calculamos el volumen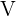 
del cilindro de radio y altura
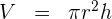
2Calculamos el volumen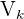 
del cilindro con el incremento de unidades en su altura
El volumen se incrementa 
veces el área de su base
¿Cuál es el volumen de un cilindro de altura 
que se incribe en una esfera de radio ?
1Calculamos el radio del cilindro inscrito en el esfera de radio , empleando el teorema de Pitágoras
2Calculamos el volumen 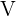del cilindro
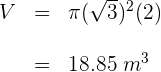
Se construye un cilindro de concreto de diámetro 
, espesor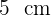 
y altura 
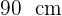. ¿Cuál es el volumen de concreto empleado para construir el cilindro?
1Calculamos el volumen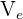 
del cilindro exterior de diámetro y altura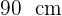
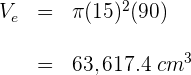
2Calculamos el volumen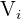 
del cilindro interior de diámetro 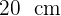y altura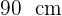
3La cantidad 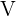de concreto empleado es
.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Necesito aprender más cosas como el teorema de pitagoras
Hola gracias por presentarnos tus inquietudes, tenemos muchos artículos de varios temas por ejemplo del teorema de Pitágoras tenemos «https://www.superprof.es/apuntes/escolar/matematicas/geometria/basica/formulas-del-teorema-de-pitagoras.html» así como varios mas, solo pon el tema en la lupa y te saldrán una gran cantidad de artículos, si tienes mas dudas menciónalo y te ayudamos.
Buenisimo. Estoy haciendo una piñata de Dobby. Y la depreesion de los ojos esta entre un cono truncado y una piramide truncada. Para hacer moldes 3 d lo importante son los angulos que se abrre la piramide desarrollada. A partir de las deformaciones del cuadrado de la base, cuanto angulo en mas o en menos le doy en el desarrollo. (Si un angulo es mas de 90 el desarrolllo de la piramide sse abre mas en angulo? O se abre menos? Yo se que pensarlo sera diverttido para vos.
Tim y Tom están intentando ganar dinero para comprar un nuevo sistema de juegos en un período de 3 meses. Tim ahorró $45,14 cada mes. Si necesitan un total de $212,94 para comprar el sistema de juegos, ¿cuánto necesita ganar Tom cada uno de los 3 meses para comprar el sistema de juegos?
holiiissssss en el primer ejercicio me sale algo diferente pero esta literalmente igual clavulado solo que el resultado es distinto, no se si es por el numero pi o porque pero vamos que no lo pillo.
Por lo general depende de cuantos decimales tomes del número pi.
La verdad no lo entendí me hubiera gustado una mejor explicación gracias
Hola te agradecemos por tu sinceridad, podrías mencionarnos que ejercicio en especial no entendiste y con gusto intentaremos dar una mejor explicación para dar un mejor servicio.