¡Bienvenidos a nuestra página dedicada a problemas de áreas y volúmenes! Aquí encontrarás una colección de desafiantes problemas matemáticos relacionados con la medición de áreas y volúmenes.
Antes que nada, debemos saber que el área es una medida que describe la extensión de una superficie bidimensional. Representa la cantidad de espacio ocupado por una figura en un plano y se expresa en unidades cuadradas, como metros cuadrados (m²) o centímetros cuadrados (cm²).
Por otro lado, el volumen es una medida que describe la cantidad de espacio tridimensional ocupado por un objeto. Representa el espacio encerrado dentro de una figura o un sólido y se expresa en unidades cúbicas, como metros cúbicos (m³) o centímetros cúbicos (cm³). Por su puesto, el área y volumen varían según el objeto.
Estas cantidades son fundamentales en muchas disciplinas, desde la arquitectura y la ingeniería hasta la física y la geometría. Aquí, te proporcionaremos explicaciones claras y paso a paso de cómo calcular el área y volumen de diferentes formas y sólidos que aparecen en problemas matemáticos y/o de la vida cotidiana.
¡Adelante! Prepárate para desarrollar tus habilidades de resolución de problemas. Disfruta y aprende de las técnicas empleadas que hemos desarrollado para ti.
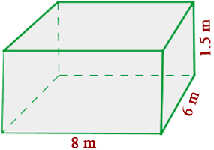
Calcula el volumen, en centímetros cúbicos, de una habitación que tiene 
m de largo, 
m de ancho y 
m de alto
1 Calculamos el volumen
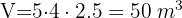
Sabiendo que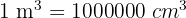 
, convertimos:
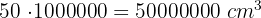
Una piscina tiene 
m de largo, 
m de ancho y 
m de profundidad. Se pinta la piscina a razón de € el metro cuadrado
A Cuánto costará pintarla.
B Cuántos litros de agua serán necesarios para llenarla.
1 Calculamos el área a pintar
2 Calculamos el costo
€
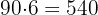3 Los litros necesarios para llenarla es el volumen de la piscina multiplicado por 1000
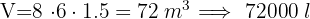
En un almacén de dimensiones m de largo, 
m de ancho y 
m de alto queremos almacenar cajas de dimensiones 
dm de largo, dm de ancho y dm de alto. ¿Cuántas cajas podremos almacenar?
1 Primeramente observamos que
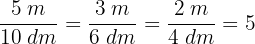
2 Calculamos el volumen del almacen
3 Calculamos el volumen de las cajas
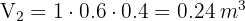
4 La cantidad de cajas se obtiene dividiendo el volumen del almacén entre el volumen de una caja
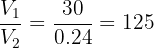cajas
1 El área total de un tetraedro es
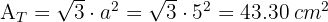
2 El área total de un octaedro es
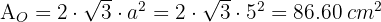
3 El área total de un icosaedro es
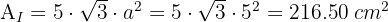
Calcula la altura de un prisma que tiene como área de la base 
dm2 y 
l de capacidad
1 Tenemos que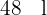 
equivalen a 
de volumen
2 Calculamos el volumen del prisma
3 Igualamos ambos volúmenes
Calcula la cantidad de hojalata que se necesitará para hacer botes de forma cilíndrica de cm de diámetro y 
cm de altura
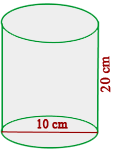
1 Calculamos el área total de un bote
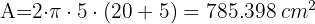
2 La cantidad empleada para 10 botes es
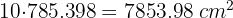
Un cilindro tiene por altura la misma longitud que la circunferencia de la base. Y la altura mide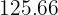 
cm. Calcular:
A El área total.
B El volumen.
1 Calculamos el radio
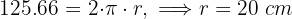
2 Calculamos el área total
3 Calculamos el volumen
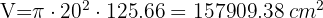
En una probeta de cm de radio se echan cuatro cubitos de hielo de cm de arista. ¿A qué altura llegará el agua cuando se derritan?
1 Calculamos el volumen de los cubos de hielo
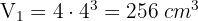
2La probeta es cilíndrica, por lo que su volumen es
3Igualamos los volúmenes y obtenemos
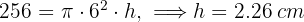
La cúpula de una catedral tiene forma semiesférica, de radio 
m. Si restaurarla tiene un coste de 
€ el m2, ¿A cuánto ascenderá el presupuesto de la restauración?
1 Calculamos el área de la semiesfera
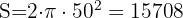
2 El costo de restauración es
€
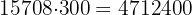¿Cuántas losetas cuadradas de cm de lado se necesitan para recubrir las caras de una piscina de m de largo por m de ancho y de m de profundidad?
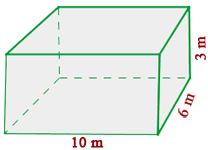
1 Calculamos el área a recubrir
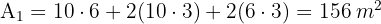
2 Calculamos el área de una loseta
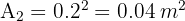
3 El número de losetas requeridas es
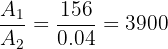
Un recipiente cilíndrico de cm de radio y cm de altura se llena de agua. Si la masa del recipiente lleno es de kg, ¿cuál es la masa del recipiente vacío?
1 Calculamos el volumen
2 El peso del recipiente es
Para una fiesta, Luis ha hecho gorros de forma cónica con cartón. ¿Cuánto cartón habrá utilizado si las dimensiones del gorro son 
cm de radio y 
cm de generatriz?
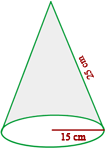
1 Calculamos el área de un cono
2 El área requerida para 10 conos es
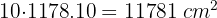
Un cubo de cm de arista está lleno de agua. ¿Cabría esta agua en una esfera de cm de radio?
1 Calculamos el volumen del cubo
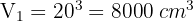
2 Calculamos el volumen e la esfera
Como el volumen de la esfera es mayor que el volumen del cubo, concluimos que si cabe el agua en la esfera.
Calcular la diagonal de un ortoedro de 10 cm de largo, cm de ancho y cm de alto
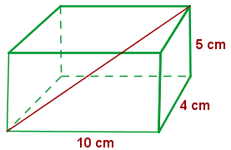
1 La diagonal viene dada por
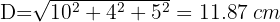
Una ésfera y un cubo son llenados de agua al mismo tiempo a razón de 1m³ por minuto. Si la ésfera tiene un radio de metros y la arista del cubo mide metros, ¿cuál se llenará primero?
Para resolver este problema debemos calcular el volumen de cada recipiente. La fórmula para el volumen de una ésfera es
Si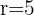 
, entonces el volumen de la ésfera es
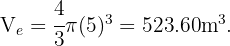
Similarmente, el volumen de un cubo de arista 
está dado por
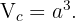
Así, si 
, entonces el volumen del cubo es
Como ambos recipientes se llenan a la misma razón de 1m³ por minuto, entonces la ésfera se llenará en aproximadamente 524 minutos o en 2 horas y 44 minutos. De igual manera, el cubo se llenará en 512 minutos o en 2 horas y 32 minutos. Por lo tanto el cubo se llenará primero de agua.
Recuerda que también puedes encontrar clases particulares de matematicas a través de nuestra plataforma si necesitas apoyo complementario.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Necesito aprender más cosas como el teorema de pitagoras
Hola gracias por presentarnos tus inquietudes, tenemos muchos artículos de varios temas por ejemplo del teorema de Pitágoras tenemos «https://www.superprof.es/apuntes/escolar/matematicas/geometria/basica/formulas-del-teorema-de-pitagoras.html» así como varios mas, solo pon el tema en la lupa y te saldrán una gran cantidad de artículos, si tienes mas dudas menciónalo y te ayudamos.
Buenisimo. Estoy haciendo una piñata de Dobby. Y la depreesion de los ojos esta entre un cono truncado y una piramide truncada. Para hacer moldes 3 d lo importante son los angulos que se abrre la piramide desarrollada. A partir de las deformaciones del cuadrado de la base, cuanto angulo en mas o en menos le doy en el desarrollo. (Si un angulo es mas de 90 el desarrolllo de la piramide sse abre mas en angulo? O se abre menos? Yo se que pensarlo sera diverttido para vos.
Tim y Tom están intentando ganar dinero para comprar un nuevo sistema de juegos en un período de 3 meses. Tim ahorró $45,14 cada mes. Si necesitan un total de $212,94 para comprar el sistema de juegos, ¿cuánto necesita ganar Tom cada uno de los 3 meses para comprar el sistema de juegos?
holiiissssss en el primer ejercicio me sale algo diferente pero esta literalmente igual clavulado solo que el resultado es distinto, no se si es por el numero pi o porque pero vamos que no lo pillo.
Por lo general depende de cuantos decimales tomes del número pi.
La verdad no lo entendí me hubiera gustado una mejor explicación gracias
Hola te agradecemos por tu sinceridad, podrías mencionarnos que ejercicio en especial no entendiste y con gusto intentaremos dar una mejor explicación para dar un mejor servicio.