Te damos la bienvenida a la segunda edición de nuestra sección dedicada a la resolución de problemas de Áreas y Volúmenes. En esta segunda entrada, exploraremos aún más a fondo el emocionante mundo de las mediciones geométricas, centrándonos en la determinación de áreas de superficies y volúmenes de sólidos.
A lo largo de esta guía, te presentaremos problemas resueltos que abarcan una amplia gama de figuras tridimensionales y bidimensionales. Cada ejemplo incluirá una descripción paso a paso de la estrategia utilizada, desde la aplicación de fórmulas específicas hasta la consideración de casos especiales que hacen que cada problema sea único.
Además, nos sumergiremos en la resolución de problemas más desafiantes que involucran la combinación de áreas y volúmenes, proporcionándote las herramientas necesarias para enfrentarte a situaciones geométricas complejas.
.
Calcula el área y el volumen de un tetraedro de 5 cm de arista.
Calcula el área y el volumen de un tetraedro de 5 cm de arista.
1 Para calcular el área total de un tetraedro usamos 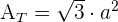
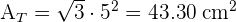
2 Para calcular el volumen de un tetraedro usamos 
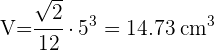
Calcular la diagonal, el área lateral, el área total y el volumen de un cubo de 5 cm de arista.
Calcular la diagonal, el área lateral, el área total y el volumen de un cubo de 5 cm de arista
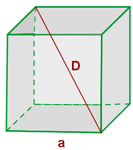
1 Para calcular la diagonal usamos 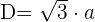
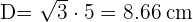
2 Para calcular el área lateral usamos 
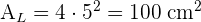
3 Para calcular el área total usamos 
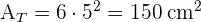
4 Para calcular el volumen usamos 
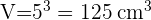
Calcula el área y el volumen de un octaedro de 5 cm de arista.
Calcula el área y el volumen de un octaedro de 5 cm de arista.
1 Para calcular el área total de un octaedro usamos 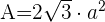
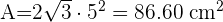
2 Para calcular el volumen de un octaedro usamos 
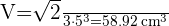
Calcula el área y el volumen de un dodecaedro de 10 cm de arista, sabiendo que la apotema de una de sus caras mide 6.88 cm.
Calcula el área y el volumen de un dodecaedro de 10 cm de arista, sabiendo que la apotema de una de sus caras mide 6.88 cm.
1 Para calcular el área total de un dodecaedro usamos 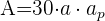
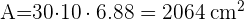
2 Para calcular el volumen de un dodecaedro usamos 
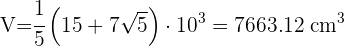
Calcula el área y el volumen de un icosaedro de 5 cm de arista.
Calcula el área y el volumen de un icosaedro de 5 cm de arista.
1 Para calcular el área total de un icosaedro usamos 
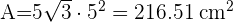
2 Para calcular el volumen de un icosaedro usamos 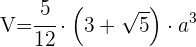

Calcula el área lateral, el área total y el volumen de un prisma cuya base es un rombo de de diagonales 12 y 18 cm.
Calcula el área lateral, el área total y el volumen de un prisma cuya base es un rombo de de diagonales 12 y 18 cm.
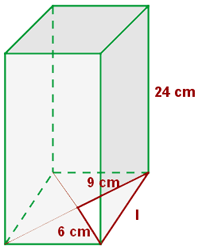
1 Al trazar las diagonales en la base se forman triángulos rectángulos por lo que podemos calcular las medidas de las aristas de la base

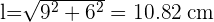
2 El área lateral es el área de los 4 rectángulos laterales

3 El área total es la suma del área lateral con las áreas de las bases
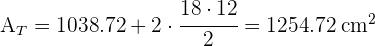
4 El volumen es igual a el área de la base multiplicada por la altura
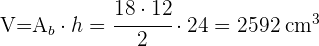
Calcula el área lateral, total y el volumen de una pirámide cuadrangular de 10 cm de arista básica y 12 cm de altura.
Calcula el área lateral, total y el volumen de una pirámide cuadrangular de 10 cm de arista básica y 12 cm de altura.
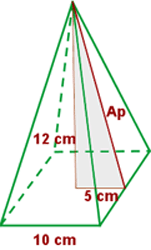
1 Calculamos la altura,  , de uno de los triángulos laterales
, de uno de los triángulos laterales
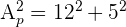
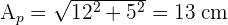
2 El área lateral es el área de los 4 triángulos laterales
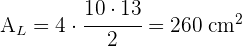
3 El área total es la suma del área lateral con el área de la base

4 El volumen de una pirámide se calcula con: 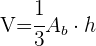
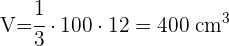
Calcula el área lateral, total y el volumen de una pirámide hexagonal de 16 cm de arista básica y 28 cm de arista lateral.
Calcula el área lateral, total y el volumen de una pirámide hexagonal de 16 cm de arista básica y 28 cm de arista lateral.
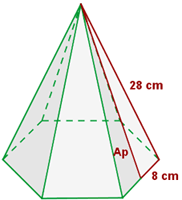
1 Calculamos la altura,  , de uno de los triángulos laterales
, de uno de los triángulos laterales
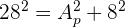
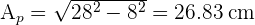
2 El área lateral es el área de los 6 triángulos laterales
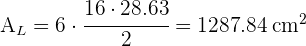
3 El área total es la suma del área lateral con el área de la base, así que debemos calcular el apotema del hexágono y luego sustituimos en la fórmula del área del hexágono
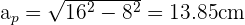
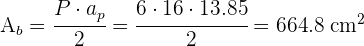
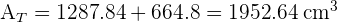
4 El volumen de una pirámide se calcula con: 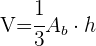 . Debemos calcular primero la altura de la pirámide:
. Debemos calcular primero la altura de la pirámide:
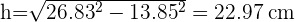
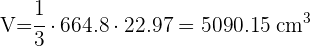
Calcular el área lateral, el área total y el volumen de un tronco de pirámide cuadrangular de aristas básicas 24 y 14 cm, y de arista lateral 13 cm.
Calcular el área lateral, el área total y el volumen de un tronco de pirámide cuadrangular de aristas básicas 24 y 14 cm, y de arista lateral 13 cm.
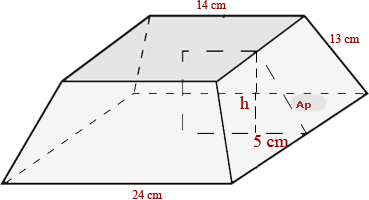
1 La apotema coincide con la altura del trapecio lateral:

2 La altura del tronco de pirámide se calcula con el teorema de Pitágoras:
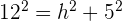
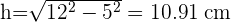
3 Calculamos el Perímetro, P, de la base mayor y el Perímetro, P', de la base menor:
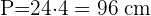

4 El área lateral se obtiene con 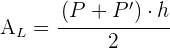 , que es equivalente a la suma de las áreas de los 4 trapecios laterales
, que es equivalente a la suma de las áreas de los 4 trapecios laterales
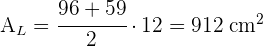
5 Calculamos el Área, A, de la base mayor y el Área, A', de la base menor y las sumamos con el área lateral para obtener el área total

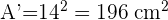

6 El volumen se calcula con 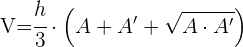
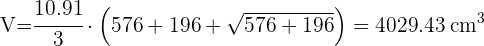
Calcula el área lateral, total y el volumen de un cono cuya generatriz mide 13 cm y el radio de la base es de 5 cm.
Calcula el área lateral, total y el volumen de un cono cuya generatriz mide 13 cm y el radio de la base es de 5 cm.
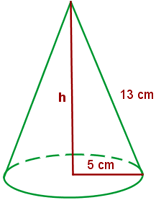
1 El área lateral se calcula con 
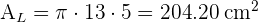
2 El área total la calculamos sumando el área lateral con el área de la base
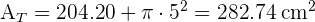
3 El volumen se calcula con 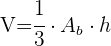 , la altura se calcula con el teorema de pitágoras
, la altura se calcula con el teorema de pitágoras

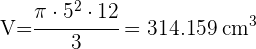
Calcula el área lateral, total y el volumen de un cono cuya altura mide 4 cm y el radio de la base es de 3 cm.
Calcula el área lateral, total y el volumen de un cono cuya altura mide 4 cm y el radio de la base es de 3 cm.
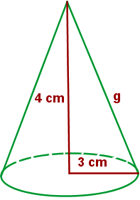
1 Calculamos la generatriz con el teorema de Pitágoras:
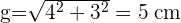
2 Calculamos el área lateral

3 Calculamos el área total:
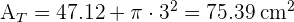
4 Calculamos el volumen
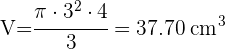
Calcular el área lateral, el área total y el volumen de un tronco de cono de radios 6 y 2 cm, y de altura 10 cm.
Calcular el área lateral, el área total y el volumen de un tronco de cono de radios 6 y 2 cm, y de altura 10 cm.
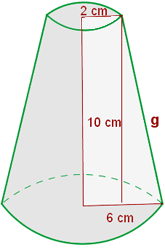
1 Calculamos la generatriz con el teorema de Pitágoras:
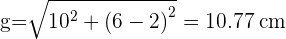
2 Calculamos el área lateral

3 Calculamos el área total:

4 Calculamos el volumen
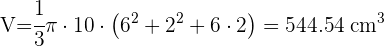
Calcular el área lateral, el área total y el volumen del tronco de cono de radios 12 y 10 cm, y de generatriz 15 cm.
Calcular el área lateral, el área total y el volumen del tronco de cono de radios 12 y 10 cm, y de generatriz 15 cm.
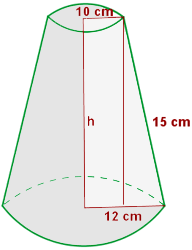
1 Calculamos la altura con el teorema de Pitágoras:

2 Calculamos el área lateral
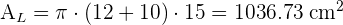
3 Calculamos el área total:
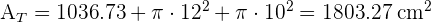
4 Calculamos el volumen
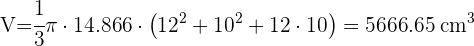
Calcular el área del círculo resultante de cortar una esfera de 35 cm de radio mediante un plano cuya distancia al centro de la esfera es de 21 cm.
Calcular el área del círculo resultante de cortar una esfera de 35 cm de radio mediante un plano cuya distancia al centro de la esfera es de 21 cm.
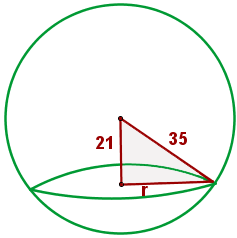
1 Calculamos el radio con el teorema de Pitágoras:

2 Calculamos el área

Calcular el área y el volumen de una esfera inscrita en un cilindro de 2 m de altura.
Calcular el área y el volumen de una esfera inscrita en un cilindro de 2 m de altura.
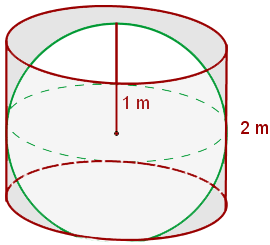
1 El radio de la esfera sería la mitad de la altura del cilindro, r=1 m, por lo que procedemos a calcular el área:
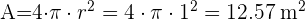
2 Calculamos el volumen:
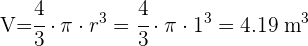
Calcular el volumen de una semiesfera de 10 cm de radio.
Calcular el volumen de una semiesfera de 10 cm de radio.
1 Una semiesfera es la mitad de una esfera por lo que su volumen sería:
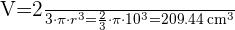
Calcular el área y el volumen de una zona esférica cuyas circunferencias tienen de radio 10 y 8 cm, y la distancia entre ellas es de 6 cm.
Calcular el área y el volumen de una zona esférica cuyas circunferencias tienen de radio 10 y 8 cm, y la distancia entre ellas es de 6cm.
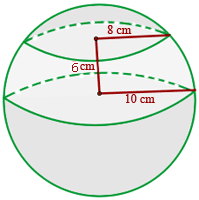
1 El área de un superficie esférica se calcula con: 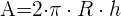

2 El volumen de un superficie esférica se calcula con: 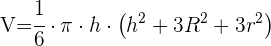
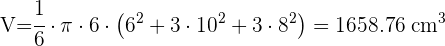
Un cubo de 20 cm de arista está lleno de agua. ¿Cabría esta agua en una esfera de 20 cm de radio?
Un cubo de 20 cm de arista está lleno de agua. ¿Cabría esta agua en una esfera de 20 cm de radio?
1 Calculamos el volumen del cubo y de la esfera y los comparamos:
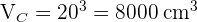

Ya que el volumen de la esfera es mayor que la del cubo, si cabe el agua en ella.
La cúpula de una catedral tiene forma semiesférica, de diámetro 50 m. Si restaurarla tiene un coste de 300 € el m2, ¿A cuánto ascenderá el presupuesto de la restauración?
La cúpula de una catedral tiene forma semiesférica, de diámetro 50 m. Si restaurarla tiene un coste de 300 € el m2, ¿A cuánto ascenderá el presupuesto de la restauración?
1 Calculamos la superficie de la semiesfera
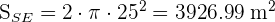
2 Multiplicamos la superficie por el costo de cada 
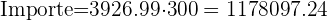
Supongamos que tenemos un cubo de lado 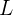 lleno de agua, y queremos vertirlo sobre una esfera de cierto radio. ¿Qué radio debe tener la esfera para que quepa exactamente el volumen del cubo?
lleno de agua, y queremos vertirlo sobre una esfera de cierto radio. ¿Qué radio debe tener la esfera para que quepa exactamente el volumen del cubo?
El volumen de un cubo de lado 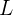 es
es 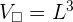 . Sea
. Sea  el radio de la esfera. Queremos encontrar una expresión para
el radio de la esfera. Queremos encontrar una expresión para  en términos de
en términos de 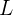 . El volumen de la esfera es
. El volumen de la esfera es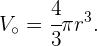
Entonces, queremos que se cumpla la ecuación
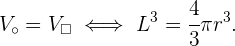
Entonces, despejamos para  .
.
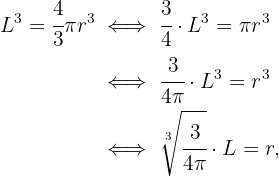
donde 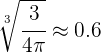 .
.
Si una bola de metal de 5 cm de radio tiene una masa de 2kg, ¿cuánta masa tiene una de 20cm de radio?
El volumen de la bola de 5 cm es
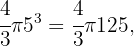
mientras que el volumen de una de 20cm es de
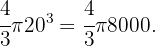
Ahora, veamos la cantidad de veces que cabe la masa de la bola pequeña en la grande:
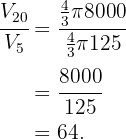
Cada una de las bolas pesa 2kg, por lo que en total son  .
.
Calcular el volumen del siguiente prisma trapezoidal:
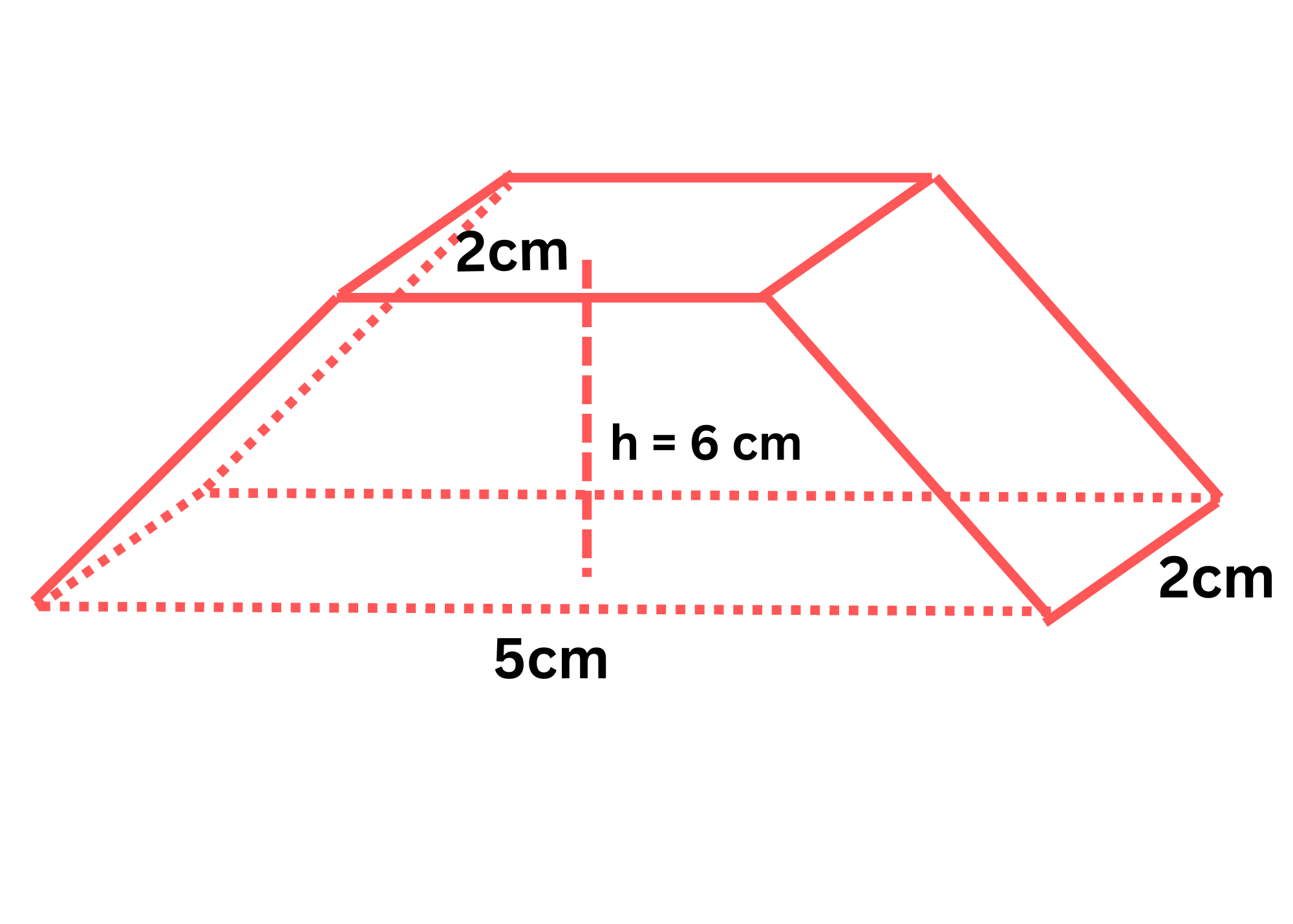
Recordemos primero que el área de un trapezoide se calcula sabiendo la base menos, mayor, y altura. En este caso, la base mayor es de 5cm, la base menor es de 2cm, y la altura es de 6cm. Entonces, su área es de
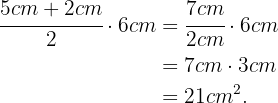
Ahora, simplemente multiplicamos esta área por la anchura, que es de 2cm, para obtener el volumen:
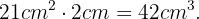
Supongamos que tenemos un vaso en forma de cono de radio  y altura
y altura  , y lo llenamos de agua. ¿Cuántos vasos necesitamos para llenar una pecera en forma de esfera con un radio de
, y lo llenamos de agua. ¿Cuántos vasos necesitamos para llenar una pecera en forma de esfera con un radio de  ?
?
El volumen de un cono es igual a
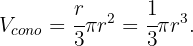
El volumen de una esfera es de
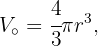
por lo que notamos que necesitamos exactamente 4 vasos para llenar la pecera, ya que
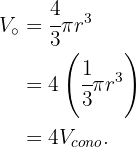
Supongamos que tenemos un vaso en forma de cilindro de radio  y altura
y altura 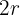 , y lo llenamos de agua. ¿Cuántos vasos necesitamos para llenar un plato hondo en forma de media esfera de radio
, y lo llenamos de agua. ¿Cuántos vasos necesitamos para llenar un plato hondo en forma de media esfera de radio  ?
?
El volumen de este cilindro es igual a
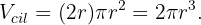
El volumen de una esfera es de
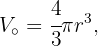
pero como necesitamos solamente la mitad de este volumen, queremos
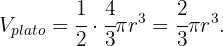
por lo que notamos que necesitamos solamente una tercera parte (1/3) de la capacidad total del vaso, ya que
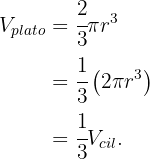
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Necesito aprender más cosas como el teorema de pitagoras
Hola gracias por presentarnos tus inquietudes, tenemos muchos artículos de varios temas por ejemplo del teorema de Pitágoras tenemos «https://www.superprof.es/apuntes/escolar/matematicas/geometria/basica/formulas-del-teorema-de-pitagoras.html» así como varios mas, solo pon el tema en la lupa y te saldrán una gran cantidad de artículos, si tienes mas dudas menciónalo y te ayudamos.
Buenisimo. Estoy haciendo una piñata de Dobby. Y la depreesion de los ojos esta entre un cono truncado y una piramide truncada. Para hacer moldes 3 d lo importante son los angulos que se abrre la piramide desarrollada. A partir de las deformaciones del cuadrado de la base, cuanto angulo en mas o en menos le doy en el desarrollo. (Si un angulo es mas de 90 el desarrolllo de la piramide sse abre mas en angulo? O se abre menos? Yo se que pensarlo sera diverttido para vos.
Tim y Tom están intentando ganar dinero para comprar un nuevo sistema de juegos en un período de 3 meses. Tim ahorró $45,14 cada mes. Si necesitan un total de $212,94 para comprar el sistema de juegos, ¿cuánto necesita ganar Tom cada uno de los 3 meses para comprar el sistema de juegos?
holiiissssss en el primer ejercicio me sale algo diferente pero esta literalmente igual clavulado solo que el resultado es distinto, no se si es por el numero pi o porque pero vamos que no lo pillo.
Por lo general depende de cuantos decimales tomes del número pi.
La verdad no lo entendí me hubiera gustado una mejor explicación gracias
Hola te agradecemos por tu sinceridad, podrías mencionarnos que ejercicio en especial no entendiste y con gusto intentaremos dar una mejor explicación para dar un mejor servicio.