
Definición de cono
Es el cuerpo de revolución obtenido al hacer girar un triángulo rectángulo alrededor de uno de sus catetos.
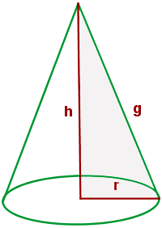
Elementos de un cono

Desarrollo del cono

Desarrollo del tronco de cono

Eje
Es el cateto fijo alrededor del cual gira el triángulo.
Bases
Es el círculo que forma el otro cateto.
Generatriz
Es la hipotenusa del triángulo rectángulo.
Por el teorema de Pitágoras la generatriz del cono será igual a:
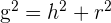
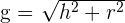
Altura
Es la distancia del vértice a la base.
Área y volumen del cono

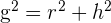
Área lateral de un cono
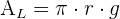
Área de un cono

Volumen de un cono
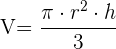
Tronco de un cono
Es el cuerpo geométrico que resulta al cortar un cono por un plano paralelo a la base y separar la parte que contiene al vértice
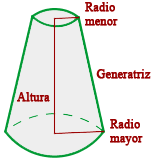
La sección determinada por al corte es la base menor
Área y volumen del tronco de cono



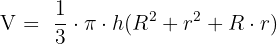
Ejercicios para practicar
Para una fiesta, Luís ha hecho 10 gorros de forma cónica con cartón. ¿Cuánto cartón habrá utilizado si las dimensiones del gorro son 15 cm de radio y 25 cm de generatriz?
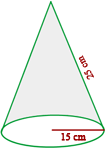
Solo necesitamos calcular el área lateral para saber cuanto cartón será utilizado.
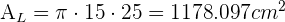
Luego lo multiplicamos por 10, ya que necesitamos 10 gorros.
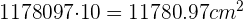
Calcula el área lateral, total y el volumen de un cono cuya generatriz mide 13 cm y el radio de la base es de 5 cm.
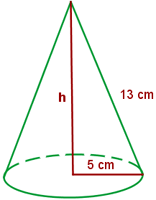
Comenzamos por calcular el área lateral,
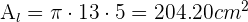
Ahora calculamos el área total,
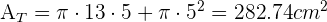
Usando la fórmula de la generatriz encontramos la altura del cono
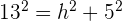

Finalmente, calculamos el volumen del cono
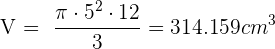
Calcula el área lateral, total y el volumen de un cono cuya altura mide 4 cm y el radio de la base es de 3 cm.
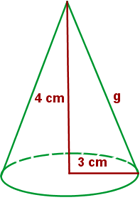
Comenzamos por encontrar el valor de la generatriz

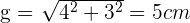
Calculamos el área lateral,
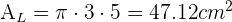
Ahora calculamos el área total,
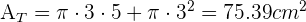
Finalmente calculamos el volumen del cono.
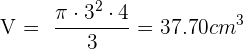
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Necesito aprender más cosas como el teorema de pitagoras
Hola gracias por presentarnos tus inquietudes, tenemos muchos artículos de varios temas por ejemplo del teorema de Pitágoras tenemos «https://www.superprof.es/apuntes/escolar/matematicas/geometria/basica/formulas-del-teorema-de-pitagoras.html» así como varios mas, solo pon el tema en la lupa y te saldrán una gran cantidad de artículos, si tienes mas dudas menciónalo y te ayudamos.
Buenisimo. Estoy haciendo una piñata de Dobby. Y la depreesion de los ojos esta entre un cono truncado y una piramide truncada. Para hacer moldes 3 d lo importante son los angulos que se abrre la piramide desarrollada. A partir de las deformaciones del cuadrado de la base, cuanto angulo en mas o en menos le doy en el desarrollo. (Si un angulo es mas de 90 el desarrolllo de la piramide sse abre mas en angulo? O se abre menos? Yo se que pensarlo sera diverttido para vos.
Tim y Tom están intentando ganar dinero para comprar un nuevo sistema de juegos en un período de 3 meses. Tim ahorró $45,14 cada mes. Si necesitan un total de $212,94 para comprar el sistema de juegos, ¿cuánto necesita ganar Tom cada uno de los 3 meses para comprar el sistema de juegos?
holiiissssss en el primer ejercicio me sale algo diferente pero esta literalmente igual clavulado solo que el resultado es distinto, no se si es por el numero pi o porque pero vamos que no lo pillo.
Por lo general depende de cuantos decimales tomes del número pi.
La verdad no lo entendí me hubiera gustado una mejor explicación gracias
Hola te agradecemos por tu sinceridad, podrías mencionarnos que ejercicio en especial no entendiste y con gusto intentaremos dar una mejor explicación para dar un mejor servicio.