Capítulos

Método de conversión de decimales a fracciones
Para convertir decimales en fracciones, hay que saber 3 cosas importantes:
- Cuando el decimal no sea periódico, dividiremos entre
1, 10, 100, ..., según sea el caso - Cuando los decimales sean periódicos, dividiremos entre
9,99,999,.., según sea el caso - Cuando existan decimales donde solo una parte es periódica
se usara como denominador el 9,90,900,..., según sea el caso
Usaremos de ejemplo estos 3 números:
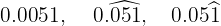
El primer caso es bastante sencillo, se trata de una cifra con 4 números
decimales y ninguno de ellos es periódico, para convertirlo a fracción
basta con escribir el 51 como numerador y en el denominador se colocara
un 1 con cuatro ceros, ya que son 4 cifras decimales, de este modo tenemos:
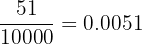
En el segundo caso, tenemos un numero con 3 cifras decimales y las 3
cifras son periódicas, entonces, tomaremos como numerador al numero 51
y como denominador colocaremos tres nueves, ya que son 3 cifras periódicas
de este modo tenemos:

En el tercer caso tenemos un numero con tres decimales, pero solo uno es
periódico, así que tomaremos como numerador el numero 51 y le restaremos
5 unidades, ya que el numero 5 que esta en los decimales, no es periódico y
como denominador colocaremos al numero 9 con dos ceros.
Recuerden que ocupamos el 9 por que hay un numero periódico y
agregamos dos ceros por que hay 2 decimales no periódicos. De
este modo tenemos:

Después, si es posible simplificamos las fracciones
Convertir los siguientes decimales a fracciones
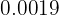
Se trata de una cifra con 4 números decimales y ninguno de ellos es periódico,
para convertirlo a fracción basta con escribir el 19 como numerador y en el
denominador se colocara un 1 con cuatro ceros, ya que son 4 cifras decimales,
de este modo tenemos:
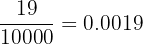
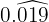
En el numerador escribimos el número sin la coma y en denominador 3 nueves
porque hay 3 cifras periódicas
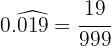
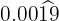
En el numerador escribimos el número sin la coma y en denominador hay dos nueves
y dos ceros porque tenemos una cifra en el período y hay dos cifras decimales
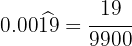
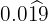
En el numerador escribimos el número sin la coma y en denominador hay dos nueves
y un cero porque tenemos dos cifras en el período y hay una cifra decimal
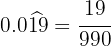
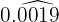
En el numerador escribimos el número sin la coma y en denominador hay cuatro nueves
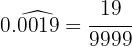
Realiza las siguientes operaciones con potencias
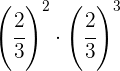
Para multiplicar potencias con la misma base se suman los exponentes
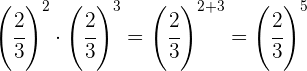
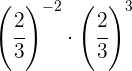
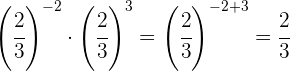
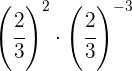
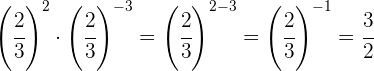
Para quitar el signo negativo del exponente tenemos que escribir la fracción inversa
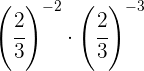
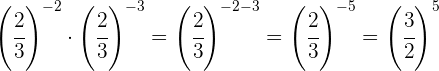
Quitamos el signo negativo del exponente tomando la fracción inversa
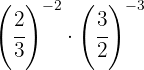
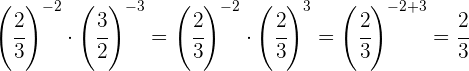
Como no tienen la misma base, tomamos la fracción inversa de la segunda potencia porque su exponente era negativo
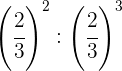
Para dividir potencias con la misma base restamos los exponentes
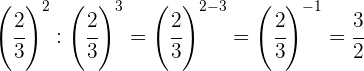
Tomamos la fracción inversa, por lo que cambiamos el signo del exponente
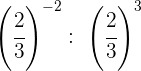
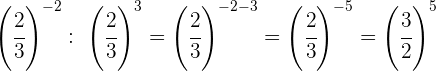
Cambiamos el signo del exponente tomando la fracción inversa
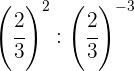
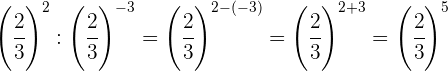
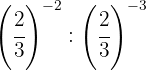
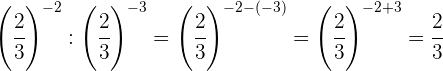
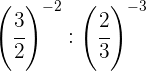
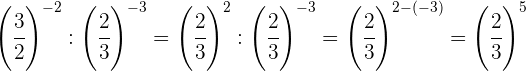
Tomamos la fracción inversa de la primera potencia para cambiar el
signo del exponente
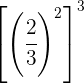
Para multiplicar potencias con la misma base se multiplican los exponentes
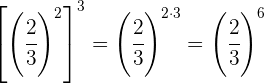
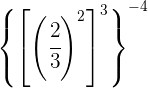
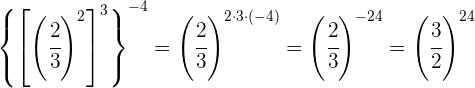
Tomamos la fracción inversa para cambiar el signo del exponente
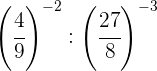
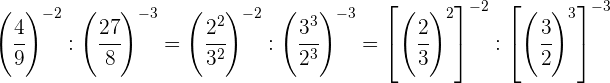
Descomponemos los números en factores, dentro de cada paréntesis
dividimos potencias con el mismo exponente, por tanto dividimos las
bases y dejamos el mismo exponente
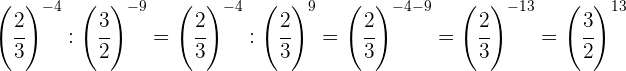
Tomamos la fracción inversa de la primera potencia para cambiar el signo del exponente y hacemos lo mismo con el resultado
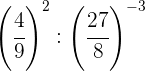
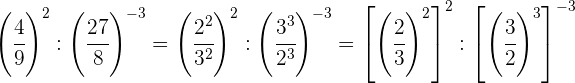
Descomponemos los números en factores, dentro de cada paréntesis
dividimos potencias con el mismo exponente, por tanto dividimos las
bases y dejamos el mismo exponente
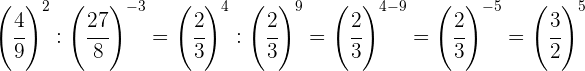
Tomamos la fracción inversa de la primera potencia para cambiar el signo del exponente y hacemos lo mismo con el resultado
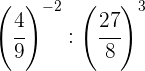
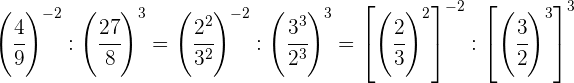
Descomponemos los números en factores, dentro de cada paréntesis
dividimos potencias con el mismo exponente, por tanto dividimos las
bases y dejamos el mismo exponente
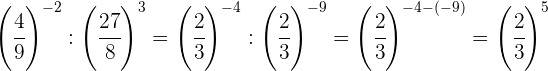
Tomamos la fracción inversa de la primera potencia para cambiar el signo del exponente y hacemos lo mismo con el resultado
Efectúa las operaciones siguientes
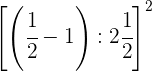
Pasamos a fracción el número mixto 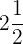 .
.
Dejamos el mismo denominador (2) y el numerador es la suma de la
multiplicación del entero (2) por el denominador (2) más el numerador
del número mixto (1).
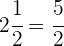
Reducimos las fracciones a su común denominador.
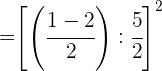
Realizamos las operaciones en los numeradores
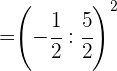
Dividimos
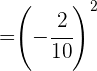
Simplificamos y realizamos la potencia
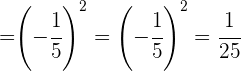
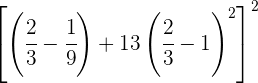
Reducimos las fracciones a su común denominador.
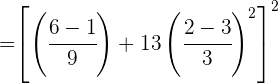
Realizamos las operaciones en los numeradores
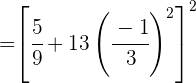
Realizamos la potencia
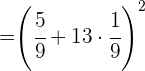
Multiplicamos
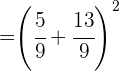
Hacemos la suma y realizamos la potencia
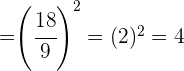
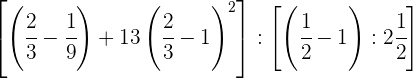
Pasamos a fracción el número mixto 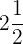 .
.
Dejamos el mismo denominador (2) y el numerador es la suma de la
multiplicación del entero (2) por el denominador (2) más el numerador
del número mixto (1).
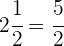
Reducimos las fracciones de cada paréntesis a su común denominador.
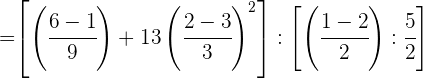
Realizamos las operaciones en los numeradores
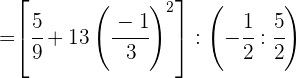
Realizamos la potencia
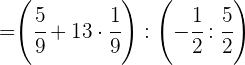
Multiplicamos en el primer paréntesis y dividimos en el 2º
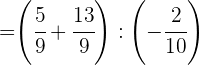
Hacemos la suma del primer paréntesis y simplificamos en el 2º
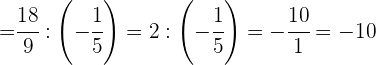
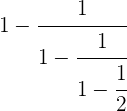
En primer lugar efectuamos la última parte del denominador
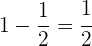
Hacemos el inverso
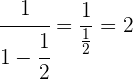
Realizamos la resta
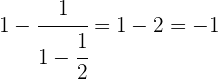
Hacemos el inverso
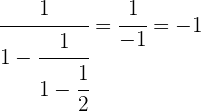
Realizamos la resta
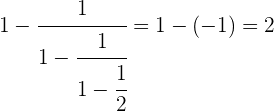
Realizando de manera consecutiva los pasos se tiene
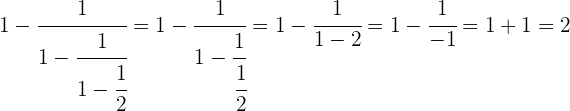
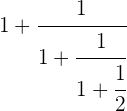
En primer lugar efectuamos la última parte del denominador
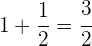
Hacemos el inverso
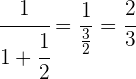
Realizamos la suma
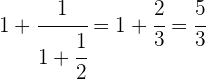
Hacemos el inverso
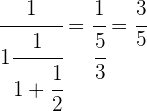
Realizamos la suma
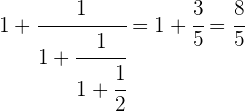
Realizando de manera consecutiva los pasos se tiene
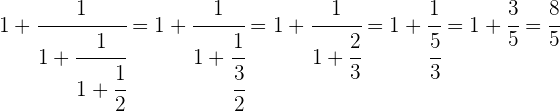
Calcula qué fracción de la unidad representa
La mitad de la mitad
La mitad de la mitad.
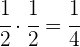
La mitad de la tercera parte
La mitad de la tercera parte.
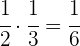
La tercera parte de la mitad
La tercera parte de la mitad.
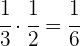
La mitad de la cuarta parte
La mitad de la cuarta parte.
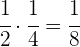
La mitad de la cuarta parte de un tercio
La mitad de la cuarta parte de un tercio.
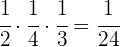
Aplicaciones
Elena va de compras con 180 €. Se gasta 3/5 de esa cantidad. ¿Cuánto le queda?
Para hallar los 3/5 de 180 tenemos que multiplicar por 3 y el resultado dividirlo por 5
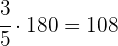 €
€
Se quedará con la cantidad original (180) menos los 3/5 gastados (108)
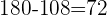 €
€
Dos automóviles A y B hacen un mismo trayecto de 572 km. El automóvil A lleva recorridos los 5/11 del trayecto cuando el B ha recorrido los 6/13 del mismo. ¿Cuál de los dos va primero? ¿Cuántos kilómetros lleva recorridos cada uno?
Vamos a comparar los recorridos de A y B, para ello vamos a poner a común denominador las fracciones, la que tenga mayor numerador será la del mayor recorrido
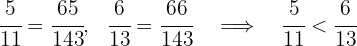
Simplificamos las fracciones y observamos que B va primero
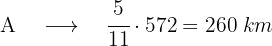
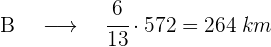
Hace unos años Pedro tenía 24 años, que representan los 2/3 de su edad actual. ¿Qué edad tiene Pedro?

24 equivale a dos partes de la edad, entonces calculamos cuánto vale
una parte (24:2) y el resultado se multiplica por el número total de partes (3)
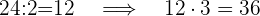 años
años
En las elecciones locales celebradas en un pueblo, 3/11 de los votos fueron para el partido A, 3/10 para el partido B, 5/14 para C y el resto para el partido D. El total de votos ha sido de 15 400. Calcular:
1 El número de votos obtenidos por cada partido.
2 El número de abstenciones sabiendo que el número de votantes representa 5/8 del censo electoral.
Calculamos los votos de cada uno de los partidos
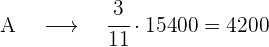 votos
votos
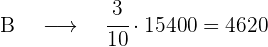 votos
votos
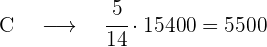 votos
votos
D tendrá el total de votos menos el número de votos conseguido por
los otros partidos
El total de votantes es 8/8, es decir, que es 1
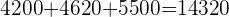
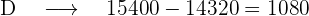
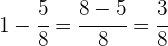

La recta está dividida en 8 partes iguales para saber la cantidad que
representa cada parte tenemos en cuenta que las 5 primeras partes
(la de los votos) suman 15 400 por tanto una parte será 15 400
dividido entre 5 que es igual a 3080. Y las otras tres partes (la de las
abstenciones) se obtendrán multiplicando 3 por 3080.
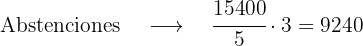
Un padre reparte entre sus hijos 1 800 €. Al mayor le da 4/9 de esa cantidad, al mediano 1/3 y al menor el resto. ¿Qué cantidad recibió cada uno?, ¿Qué fracción del dinero recibió el tercero?
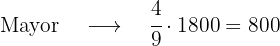
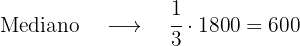
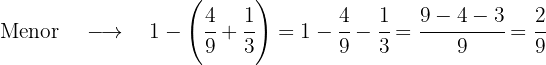
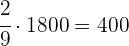
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Si van a poner ejercicio pónganlo bien si van a poner división póngame en el signo de división si van a poner multiplicación ponga bien el signo de multiplicación
Fracciónes y la unidad que representan problemas de la vida diaria usando las fracciones y las unidades que representan
La mitad y la mitad
En otro problema podemos ver qué está fracciones y litros ahí podemos ver los litros de agua y que tienes que saber cuántos litros de agua quedan
Por lo tanto quedan 90 litros de agua en el tanque
Hola, muchas gracias por tu aportación.
Hola lamentamos los errores cometidos, podrías hacernos el favor de mencionarnos donde están las fallas para poder corregirlas.
En el ejercicio dos no da esa respuesta
Hola el artículo que revise hay varios ejercicios 2, pero no encontré el error que mencionas, podrías dar mas detalles por favor, así se podrá corregir.