Pasos a seguir para resolver operaciones con fracciones
1 Pasar a fracción impropia los números mixtos y decimales.
2 Si aparece una fracción impropia con potencia o raíz, resuévela
3 Efectuar las operaciones entre paréntesis, corchetes y llaves, de dentro hacia afuera.
Considerar la siguiente prioridad
Primero productos y cocientes, de izquierda a derecha.
Al final las sumas y restas.
Ejemplo 1
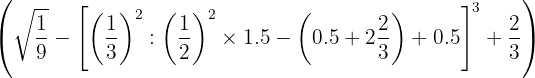
1Convertimos números mixtos o con decimales (Paso 1)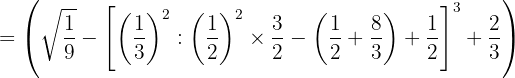
2Calculamos potencias o raices (Paso 2)
3Resolvemos los parentesis de más "adentro" (Paso 3)
Es decir, desarrollaremos los paréntesis que cumplen que dentro de ellos no hay más paréntesis. No olvidemos considerar la prioridad de operaciones.
En este caso: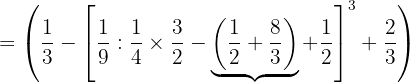
Así obtenemos la expresión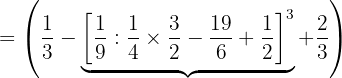
4Desarrollamos considerando nuevamente los pasos hasta finalizar
Basándonos en prioridad de operaciones, resolvemos primero las multiplicaciones y divisiones de izquierda a derecha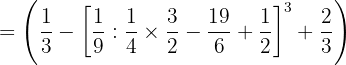
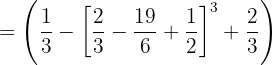
Luego las sumas y restas.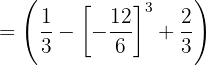
Aplicando una vez más los pasos, nos deshacemos del paréntesis calculando la potencia y tomando en cuenta la ley de los signos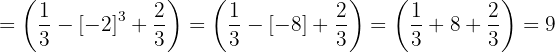
Ejemplo 2
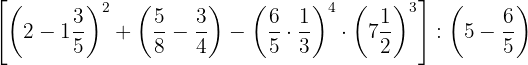
1 Convertimos números mixtos o con decimales (Paso 1)
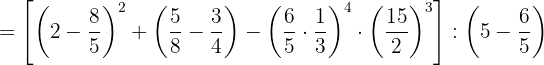
2 Resolvemos potencias o raices (Paso 2)
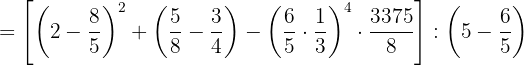
3 Resolvemos los parentesis de más "adentro" (Paso 3)
En este caso, podemos proceder con los siguientes paréntesis
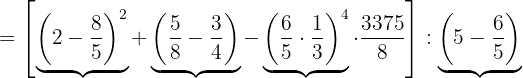
En cada uno de ellos, debemos considerar la prioridad de operaciones.
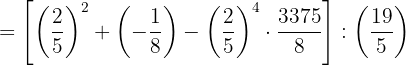
4 Desarrollamos considerando nuevamente los pasos hasta finalizar
Elevamos las potencias
Por prioridad de operaciones, (realizando primero la multiplicación y simplificando)
Realizamos las sumas y restas en el paréntesis poniendo a común denominador
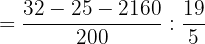
Sumando los terminos, desarrollando el cociente y simplificando se obtiene:
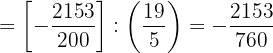
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Hagan ejercicios de muchas multiplicaciones, divisiones y potencias
Hola te agradecemos tu sugerencia, en el buscador puedes poner multiplicaciones, divisiones y potencia, entonces van aparecer muchos artículos con gran variedad de ejercicios, pruébalo y no te arrenpentiras.
el ejercicio 6 esta mal hecho la respuesta no coincide
Hola si es el problema de los votos, revise y no encontré el error pues el inciso a) difiere del inciso b), pero si puedes ser mas especifico y darme mas detalles podría darme una explicación mas completa.
No me dejó acomodar las dos primeras imágenes
Hola otra vez, revise lo que mencionas si te refieres a mover fracciones, tienes que hacerlo con cuidado pues si lo haces muy rápido no te deja, ya lo hice yo y si pude, pero tuve que ser cuidadoso.
Hola una disculpa por el fallo, estamos trabajando en la mejora de la plataforma, por favor ten un poco de paciencia para que este tipo de errores desaparezcan.
El ejercicio 10 de Simplificación de Fracciones esta mal hecho. En la multiplicación de fracciones se multiplica numero con numerador y denominado con denominador, no se suma nada. Habéis cometido un error
Hola tienes razón en la multiplicación de fracciones se multiplica de manera directa numerador por numerador y denominador por denominador, pero no encontré el error que mencionas, podrías dar mas detalles por favor.