Capítulos
Las fracciones son una de las bases fundamentales de las matemáticas, utilizadas para representar partes de un todo. El manejo adecuado de las fracciones es esencial en diversos campos, ya que nos permite resolver problemas en situaciones cotidianas y académicas, tales como la división de cantidades, la comparación de proporciones y la simplificación de expresiones matemáticas.
En este conjunto de ejercicios resueltos, se abordan diferentes tipos de problemas relacionados con las fracciones, incluyendo operaciones como suma, resta, multiplicación, división, simplificación y conversión entre fracciones y decimales. Cada ejercicio está acompañado de una explicación detallada de los pasos a seguir para obtener la solución correcta, lo que permite una comprensión profunda de los procedimientos involucrados.

Problemas de la vida diaria
Pedro tiene 500 € y destina  partes para alimentos. ¿Cuánto le queda después de comprar sus alimentos?
partes para alimentos. ¿Cuánto le queda después de comprar sus alimentos?
Gasto en alimentos 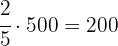 €
€
Dineros restante 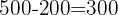 €
€
Un árbol de manzana tiene 350 frutos. Durante una lluvia intensa, se pierde  de los frutos cayendo del manzano. ¿Cuántas manzanas quedan en el árbol después de la lluvia?
de los frutos cayendo del manzano. ¿Cuántas manzanas quedan en el árbol después de la lluvia?
Manzanas caidas 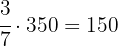
Manzanas restantes en el árbol 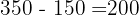
Un depósito de agua contiene 1000 litros, de los cuales  es empleado para regar las plantas del jardín y el restante para para el consumo del hogar. ¿Qué cantidad está destinada para el consumo de la casa?
es empleado para regar las plantas del jardín y el restante para para el consumo del hogar. ¿Qué cantidad está destinada para el consumo de la casa?
Agua empleada para regar el jardín 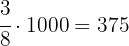 litros
litros
Agua para el consumo de la casa  litros
litros
Alicia dispone de  € para compras. El jueves gastó
€ para compras. El jueves gastó  de esa cantidad y el sábado los
de esa cantidad y el sábado los  de lo que le quedaba. ¿Cuánto gastó cada día y cuánto le queda al final?
de lo que le quedaba. ¿Cuánto gastó cada día y cuánto le queda al final?
Gasto del jueves 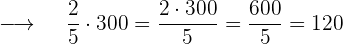 €
€
Dinero restante  €
€
Gasto del sabado 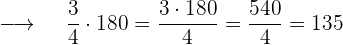 €
€
Dinero restante final  €
€
De los ingresos de una comunidad de vecinos se emplean  en combustible,
en combustible,  se emplea en electricidad,
se emplea en electricidad, 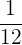 en la recogida de basuras,
en la recogida de basuras,  en mantenimiento del edificio y el resto se emplea en limpieza.
en mantenimiento del edificio y el resto se emplea en limpieza.
¿Qué fracción de los ingresos se emplea en limpieza?
De acuerdo con la fracción de ingresos empleada, ordena las partidas enumeradas de menor a mayor.
1 Encontrar una expresión que relacione los datos y desarrollar
Sea  la fracción de dinero usado en limpieza
la fracción de dinero usado en limpieza
Se utiliza todo el dinero por lo que las fracciones del dinero empleadas en cada gasto deben sumar  .
.
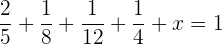
Buscamos el minimo común múltiplo de los denominadores

Se obtienen fracciones equivalentes al dividir el m.c.m entre el denominador, el número resultante multiplicarlo por el numerador, y poner al m.c.m como denominador.
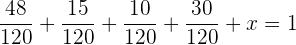
Sumamos las fracciones


Despejamos la

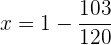
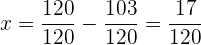
Finalmente, se gastó 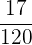 en limpieza
en limpieza
2 Ordenar las fracciones
Para ordenar las fracciones tenemos que reducir a común denominador, que ya lo hemos hecho al realizar la suma
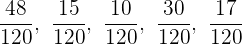
Ordenadas quedarían así
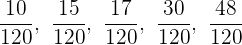
Simplificamos a las fracciones originales que teníamos
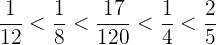
Pasar de decimal a fracción
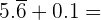
En este ejercicio tenemos sumas de decimales exactos, peródicos puros y mixtos, que los pasaremos a sus respectivas fracciones.
Si la fracción es decimal exacta, la fracción tiene como numerador el número dado sin la coma, y por denominador, la unidad seguida de tantos ceros como cifras decimales tenga.
Si la fracción es periódica pura, la fracción generatriz tiene cómo numerador el número dado sin la coma, menos la parte entera, y por denominador un número formado por tantos nueves como cifras tenga el período.
Si la fracción es periódica mixta, la fracción generatriz tiene como numerador el número dado sin la coma, menos la parte entera seguida de las cifras decimales no periódicas, y por denominador, un número formado por tantos nueves como cifras tenga el período, seguidos de tantos ceros como cifras tenga la parte decimal no periódica.
Entonces,
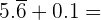
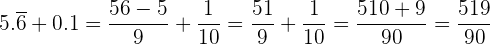

En este ejercicio tenemos sumas de decimales exactos, peródicos puros y mixtos, que los pasaremos a sus respectivas fracciones.
Si la fracción es decimal exacta, la fracción tiene como numerador el número dado sin la coma, y por denominador, la unidad seguida de tantos ceros como cifras decimales tenga.
Si la fracción es periódica pura, la fracción generatriz tiene cómo numerador el número dado sin la coma, menos la parte entera, y por denominador un número formado por tantos nueves como cifras tenga el período.
Si la fracción es periódica mixta, la fracción generatriz tiene como numerador el número dado sin la coma, menos la parte entera seguida de las cifras decimales no periódicas, y por denominador, un número formado por tantos nueves como cifras tenga el período, seguidos de tantos ceros como cifras tenga la parte decimal no periódica.
Entonces,

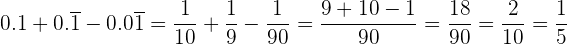

En este ejercicio tenemos sumas de decimales exactos, peródicos puros y mixtos, que los pasaremos a sus respectivas fracciones.
Si la fracción es decimal exacta, la fracción tiene como numerador el número dado sin la coma, y por denominador, la unidad seguida de tantos ceros como cifras decimales tenga.
Si la fracción es periódica pura, la fracción generatriz tiene cómo numerador el número dado sin la coma, menos la parte entera, y por denominador un número formado por tantos nueves como cifras tenga el período.
Si la fracción es periódica mixta, la fracción generatriz tiene como numerador el número dado sin la coma, menos la parte entera seguida de las cifras decimales no periódicas, y por denominador, un número formado por tantos nueves como cifras tenga el período, seguidos de tantos ceros como cifras tenga la parte decimal no periódica.
Entonces,

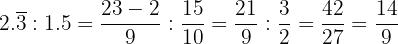
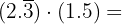
En este ejercicio tenemos sumas de decimales exactos, peródicos puros y mixtos, que los pasaremos a sus respectivas fracciones.
Si la fracción es decimal exacta, la fracción tiene como numerador el número dado sin la coma, y por denominador, la unidad seguida de tantos ceros como cifras decimales tenga.
Si la fracción es periódica pura, la fracción generatriz tiene cómo numerador el número dado sin la coma, menos la parte entera, y por denominador un número formado por tantos nueves como cifras tenga el período.
Si la fracción es periódica mixta, la fracción generatriz tiene como numerador el número dado sin la coma, menos la parte entera seguida de las cifras decimales no periódicas, y por denominador, un número formado por tantos nueves como cifras tenga el período, seguidos de tantos ceros como cifras tenga la parte decimal no periódica.
Entonces,
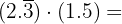
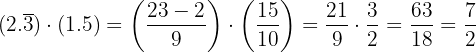
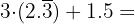
En este ejercicio tenemos sumas de decimales exactos, peródicos puros y mixtos, que los pasaremos a sus respectivas fracciones.
Si la fracción es decimal exacta, la fracción tiene como numerador el número dado sin la coma, y por denominador, la unidad seguida de tantos ceros como cifras decimales tenga.
Si la fracción es periódica pura, la fracción generatriz tiene cómo numerador el número dado sin la coma, menos la parte entera, y por denominador un número formado por tantos nueves como cifras tenga el período.
Si la fracción es periódica mixta, la fracción generatriz tiene como numerador el número dado sin la coma, menos la parte entera seguida de las cifras decimales no periódicas, y por denominador, un número formado por tantos nueves como cifras tenga el período, seguidos de tantos ceros como cifras tenga la parte decimal no periódica.
Entonces,
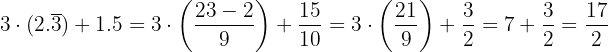
Ejercicios de operaciones combinadas
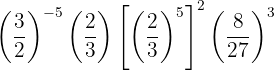
Trataremos de poner todas las fracciones con el mismo numerador y denominador, para ello descomponemos en factores los números que no sean primos
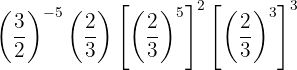
Aplicamos ley de los exponentes, pues es una potencia de potencia de fracción, los exponentes se multiplican
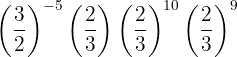
Para pasar de una potencia con exponente negativo a exponente positivo tenemos que hacer la inversa de la fracción
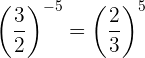
Entonces
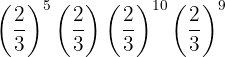
Multiplicamos las potencias con la misma base y dividimos los resultados
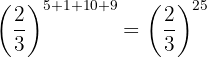
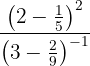
Realizamos las operaciones indicadas en los paréntesis.

Efectuamos las operaciones indicadas y simplificamos
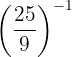
Tenemos en cuenta que en una fracción elevada a un número negativo tenemos que cambiar el numerador por el denominador y posteriormente elevar al exponente
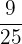
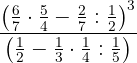
Realizamos las operaciones indicadas en los paréntesis. En el paréntesis del denominador tenemos que multiplicar primero y en siguiente paso dividimos.
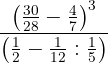
Efectuamos las operaciones indicadas y simplificamos
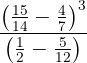
Realizamos las operaciones indicadas y reducimos a común denominador

Efecuamos la operaciones y simplificamos
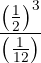
Realizamos la potencias
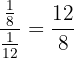
Simplificamos

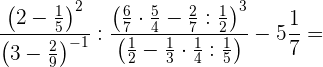
Realizamos las operaciones indicadas en los paréntesis. En el paréntesis del segundo denominador tenemos que multiplicar primero y en siguiente paso dividimos.
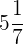 es un número mixto por tanto dejamos el mismo denominador
es un número mixto por tanto dejamos el mismo denominador  y el numerador es la suma de la multiplicación del entero
y el numerador es la suma de la multiplicación del entero  , por el denominador
, por el denominador  más el numerador del número mixto
más el numerador del número mixto  .
.
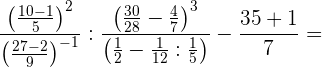
Efectuamos las operaciones indicadas y simplificamos 
Realizamos las operaciones indicadas y reducimos a común denominador en la segunda fracción

Efecuamos la operaciones en la segunda fracción y simplificamos

Realizamos la potencias y tenemos en cuenta que en una fracción elevada a un número negativo tenemos que cambiar el numerador por el denominador y posteriormente elevar al exponente
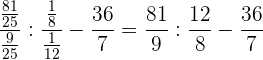
En el paso anterior operamos teniendo en cuenta que:
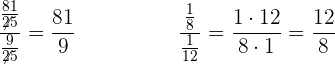
Simplificamos y operamos.
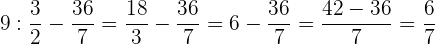
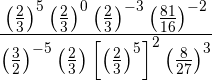
Trataremos de poner todas las fracciones con el mismo numerador y denominador, para ello descomponemos en factores los números que no sean primos

Aplicamos ley de los exponentes, pues es una potencia de potencia de fracción, los exponentes se multiplican
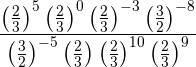
Para pasar de una potencia con exponente negativo a exponente positivo tenemos que hacer la inversa de la fracción
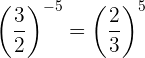

Entonces
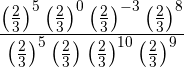
Tanto en el numerador como en el denominador multiplicamos las potencias con la misma base y dividimos los resultados
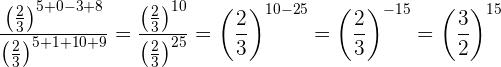
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Si van a poner ejercicio pónganlo bien si van a poner división póngame en el signo de división si van a poner multiplicación ponga bien el signo de multiplicación
Fracciónes y la unidad que representan problemas de la vida diaria usando las fracciones y las unidades que representan
La mitad y la mitad
En otro problema podemos ver qué está fracciones y litros ahí podemos ver los litros de agua y que tienes que saber cuántos litros de agua quedan
Por lo tanto quedan 90 litros de agua en el tanque
Hola, muchas gracias por tu aportación.
Hola lamentamos los errores cometidos, podrías hacernos el favor de mencionarnos donde están las fallas para poder corregirlas.
En el ejercicio dos no da esa respuesta
Hola el artículo que revise hay varios ejercicios 2, pero no encontré el error que mencionas, podrías dar mas detalles por favor, así se podrá corregir.