Repaso de las leyes de los exponentes
1
2
3
4
5
6
Ejercicios propuestos
Simplifica empleando las leyes de los exponentes
1 
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
Para multiplicar potencias con la misma base dejamos la misma base y sumamos los exponentes
2
Para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
3
Para hallar la potencia de una potencia multiplicamos los exponentes
4
Para hallar la potencia de un producto, elevamos cada alemento a la potencia dada
5
Para hallar la potencia de una potencia multiplicamos los exponentes
6
Para hallar la potencia de una potencia multiplicamos los exponentes
7
Primero expresamos la base como producto de números primo y luego hallamos la potencia de una potencia multiplicando los exponentes
8
Primero expresamos la base como producto de números primo y luego hallamos la potencia de una potencia multiplicando los exponentes
9
Para multiplicar potencias con la misma base dejamos la misma base y sumamos los exponentes
10
Para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
11
Hallamos la potencia de una potencia multiplicando los exponentes
12
Para hallar la potencia de un producto, elevamos cada elemento a la potencia dada
13
Para hallar la potencia de una potencia multiplicamos los exponentes
14
Primero hallamos la potencia de una potencia multiplicando los exponentes y aplicamos que todo número distinto de cero elevado a la potencia cero es igual a uno
15
Primero expresamos la base como producto de números primos y luego hallamos la potencia de una potencia multiplicando los exponentes
16
Primero expresamos la base como producto de números primos y luego hallamos la potencia de una potencia multiplicando los exponentes
Realizar las siguientes operaciones con potencias:
1
2
3
4
5
6
7
8
9
10
1
Para multiplicar potencias con la misma base dejamos la misma base y sumamos los exponentes
El resultado tendrá signo negativo porque la base es negativa y el exponente es impar
2
Primero hemos descompuesto 8 en factores y luego multiplicamos potencias con la misma base
El resultado tendrá signo positivo porque la base es negativa y el exponente es par
3
Para multiplicar potencias con la misma base dejamos la misma base y sumamos los exponentes
El resultado tendrá signo negativo porque la base es negativa y el exponente es impar
4
Para multiplicar potencias con la misma base dejamos la misma base y sumamos los exponentes
Al ser negativo el exponente, tenemos que tomar el inverso de la base
5
Para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
Al ser negativo el exponente, tenemos que tomar el inverso de la base
6
Para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
Al ser negativo el exponente, tenemos que tomar el inverso de la base con exponente positivo y desarrollamos
7
Para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
8
Para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
9
Para elevar una potencia a una potencia dejamos la misma base y multiplicamos los exponentes
Para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
10
Resolvemos los corchetes por lo que para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
Para elevar una potencia a una potencia dejamos la misma base y multiplicamos los exponentes
El resultado tendrá signo positivo porque la base es negativa y el exponente es par
Realizar las siguientes operaciones con potencias:
1
2
3 
4
5
6
7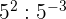
8
9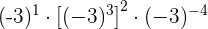
10
1
Para multiplicar potencias con la misma base dejamos la misma base y sumamos los exponentes
El resultado tendrá signo positivo porque la base es negativa y el exponente es par
2
Primero hemos descompuesto 27 en factores y luego multiplicamos potencias con la misma base
El resultado tendrá signo positivo porque la base es negativa y el exponente es par
3
Para multiplicar potencias con la misma base dejamos la misma base y sumamos los exponentes
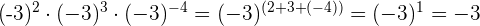
El resultado tendrá signo negativo porque la base es negativa y el exponente es impar
4
Para multiplicar potencias con la misma base dejamos la misma base y sumamos los exponentes
Al ser negativo el exponente, tenemos que tomar el inverso de la base con exponente positivo y luego desarrollamos
5
Para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
Al ser negativo el exponente, tenemos que tomar el inverso de la base
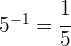
6
Para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
Al ser negativo el exponente, tenemos que tomar el inverso de la base con exponente positivo y desarrollamos
7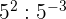
Para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
8
Para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
9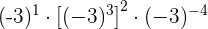
Para elevar una potencia a una potencia dejamos la misma base y multiplicamos los exponentes
Para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
El resultado tendrá signo negativo porque la base es negativa y el exponente es impar
10
Resolvemos los corchetes por lo que para dividir potencias con la misma base dejamos la misma base y restamos los exponentes
Para elevar una potencia a una potencia dejamos la misma base y multiplicamos los exponentes
El resultado tendrá signo negativo porque la base es negativa y el exponente es impar
Realizar las siguientes operaciones con potencias:
1
2
3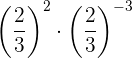
4
5
6
7
8
9
10
11
12
13
1
Como se trata de multiplicar potencias con la misma base, se conserva la base y sumamos los exponentes
2
Como se trata de multiplicar potencias con la misma base, se conserva la base y sumamos los exponentes
Como la potencia resultante tiene exponente uno, entonces la potencia es igual a la base
3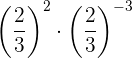
Como se trata de multiplicar potencias con la misma base, se conserva la base y sumamos los exponentes
Como la potencia resultante tiene exponente negativo, entonces la potencia es igual al inverso de la base con exponente positivo. Finalmente la potencia resultante tiene exponente uno, entonces la potencia es igual a la nueva base
4
Como se trata de multiplicar potencias con la misma base, se conserva la base y sumamos los exponentes
Como la potencia resultante tiene exponente negativo, entonces la potencia es igual al inverso de la base con exponente positivo.
5
Cambiamos el segundo elemento a exponente positivo, para ello la base cambia por su inversa y resolvemos la multiplicación de potencias con la misma base
La potencia resultante tiene exponente uno, entonces la potencia es igual a la base
6
Como se trata de dividir potencias con la misma base, se conserva la base y restamos los exponentes
Como la potencia resultante tiene exponente negativo, entonces la potencia es igual al inverso de la base con exponente positivo. Finalmente como la potencia resultante tiene exponente uno, entonces la potencia es igual a la nueva base
7
Como se trata de dividir potencias con la misma base, se conserva la base y restamos los exponentes
Como la potencia resultante tiene exponente negativo, entonces la potencia es igual al inverso de la base con exponente positivo.
8
Como se trata de dividir potencias con la misma base, se conserva la base y restamos los exponentes
9
Como se trata de dividir potencias con la misma base, se conserva la base y restamos los exponentes
Como la potencia resultante tiene exponente uno, entonces la potencia es igual a la nueva base
10
Cambiamos el primer elemento a exponente positivo, para ello la base cambia por su inversa y resolvemos la división de potencias con la misma base
11
Como se trata de potencia de una potencias, se conserva la base y multiplicamos los exponentes
12
Como se trata de potencia de una potencias, se conserva la base y multiplicamos los exponentes
Como la potencia resultante tiene exponente negativo, entonces la potencia es igual al inverso de la base con exponente positivo.
13
Expresamos como potencias de números primos las bases de las potencias
Cambiamos el primer elemento a exponente positivo, para ello la base cambia por su inversa y resolvemos la división de potencias con la misma base
Simplifica la siguiente expresión:
1Ponemos todas las fracciones con el mismo numerador y denominador, para ello descomponemos en factores los números que no sean primos
2Se tienen elementos que son potencias de potencias, entonces se conserva la base y se multiplican los exponentes
3Para las potencias con base 
y exponentes negativos, ponemos la fracción inversa con exponente positivo
4Tanto en el numerador como en el denominador multiplicamos las potencias con la misma base y dividimos los resultados. Finalmente, ponemos la fracción inversa con exponente positivo
Simplifica la siguiente expresión:
1Realizamos primeramente las multiplicaciones y divisiones dentro de los paréntesis
2Simplificamos aquellas fracciones donde sea posible realizarlo, reescribimos las fracciones mixtas y después calculamos la suma en los paréntesis
3Reescribimos la última expresión y aplicamos las propiedades de las potencias de números racionales
4Realizamos las divisiones y simplificamos. Finalmente realizamos la rsta de las fracciones resultantes
Calcula los valores de las siguientes potencias:
1 
2 
3 
4 
1
Una potencia con exponente fraccionario es igual a una raíz cuyo índice es el denominador de la fracción y el exponente del radicando es el numerador. Descomponemos 
en factores, efectuamos las operaciones en el radicando y extraemos factores
2
Descomponemos 
en factores, efectuamos las operaciones en el radicando y extraemos factores
3
En este caso pasamos el exponente que es un número decimal exacto a fracción, efectuamos las operaciones en el radicando y extraemos factores
4 
El exponente que es un periódico puro lo pasamos a fracción.
Sustituimos, efectuamos las operaciones en el radicando y extraemos factores
¿Qué te parece un repaso personalizado a través de unas clases particulares de matematicas?
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Si van a poner ejercicio pónganlo bien si van a poner división póngame en el signo de división si van a poner multiplicación ponga bien el signo de multiplicación
Hola lamentamos los errores cometidos, podrías hacernos el favor de mencionarnos donde están las fallas para poder corregirlas.
En el ejercicio dos no da esa respuesta
Hola el artículo que revise hay varios ejercicios 2, pero no encontré el error que mencionas, podrías dar mas detalles por favor, así se podrá corregir.
Buenos días, saludos desde México, quiero hacerle la observación de que el resultado del inciso b del problema 6 de la primera sección es incorrecto, porque está considerando al censo como 15,400 y no es verdad, ese es el número de votantes, por tanto el censo debe tener mayor cantidad de personas
Hola gracias por visitar la pagina, una disculpa ya se corrigió.
Hola agradecemos tu observación, una disculpa ya se corrigió.