Fracciones propias
Las fracciones propias son aquellas cuyo numerador es menor que el denominador. Su valor está comprendido entre cero y uno.
Ejemplo:
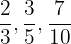
Fracciones impropias
Las fracciones impropias son aquellas cuyo numerador es mayor que el denominador. Su valor es mayor que 1.
Ejemplo:
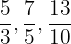
Número mixto
El número mixto o fracción mixta está compuesto de una parte entera y otra fraccionaria.
Para pasar de número mixto a fracción impropia:
1 Se deja el mismo denominador
2 El numerador se obtiene de la suma del producto del entero por el denominador más el numerador, del número mixto.
Ejemplo:
Para pasar una fracción impropia a número mixto:
1 Se divide el numerador por el denominador.
2 El cociente es el entero del número mixto.
3 El resto es el numerador de la fracción.
4 El denominador es el mismo que el de la fracción impropia.
Ejemplo:
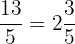
Fracciones decimales
Las fracciones decimales tienen como denominador una potencia de 10.
Ejemplo:
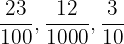
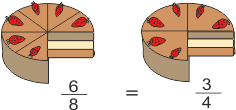
Fracciones equivalentes
Dos fracciones son equivalentes cuando el producto de extremos es igual al producto de medios
y 
son los extremos
y 
son los medios
Ejemplo:
Calcula si son equivalentes las fracciones 
y 
entonces si son equivalentes.
Si se multiplica o divide el numerador y denominador de una fracción por un número entero, distinto de cero, se obtiene otra fracción equivalente a la dada.
Al primer caso le llamamos ampliar o amplificar.
Ejemplo:
Simplificar fracciones
Simplificar una fracción es transformarla en una fracción equivalente más simple.
1 Para simplificar una fracción dividimos numerador y denominador por un mismo número.
2 Empezaremos a simplificar probando por los primeros números primos: 2, 3, 5, 7, ... Es decir, probamos a dividir numerador y denominador entre 2 mientras se pueda, después pasamos al 3 y así sucesivamente.
3 Se repite el proceso hasta que no haya más divisores comunes.
4 Si los términos de la fracción terminan en ceros, empezaremos quitando los ceros comunes finales del numerador y denominador, lo cual es equivalente a dividir numerador y denominador por la misma potencia de 10.
5 Si el número por el que dividimos es el máximo común divisor del numerador y denominador llegamos a una fracción irreducible que es equivalente a la inicial.
Ejemplo:
Fracciones irreducibles
Las fracciones irreducibles son aquellas que no se pueden simplificar, esto sucede cuando el numerador y el denominador son primos entre sí, o lo que es lo mismo, cuando el mcd de ambos números es 1.
Ejemplo:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Si van a poner ejercicio pónganlo bien si van a poner división póngame en el signo de división si van a poner multiplicación ponga bien el signo de multiplicación
Fracciónes y la unidad que representan problemas de la vida diaria usando las fracciones y las unidades que representan
La mitad y la mitad
En otro problema podemos ver qué está fracciones y litros ahí podemos ver los litros de agua y que tienes que saber cuántos litros de agua quedan
Por lo tanto quedan 90 litros de agua en el tanque
Hola, muchas gracias por tu aportación.
Hola lamentamos los errores cometidos, podrías hacernos el favor de mencionarnos donde están las fallas para poder corregirlas.
En el ejercicio dos no da esa respuesta
Hola el artículo que revise hay varios ejercicios 2, pero no encontré el error que mencionas, podrías dar mas detalles por favor, así se podrá corregir.