Capítulos
¡Bienvenido a los emocionantes ejercicios de operaciones con fracciones! En esta serie de desafíos matemáticos, exploraremos el fascinante mundo de las fracciones y aprenderemos cómo realizar diversas operaciones con ellas.
Las fracciones son una parte esencial de las matemáticas y tienen una amplia aplicación en la vida cotidiana, desde la cocina y la construcción hasta las finanzas y la ciencia. Durante esta práctica, dominaremos las operaciones fundamentales con fracciones, como la suma, resta, multiplicación y división.
Ya sea que estés buscando mejorar tus habilidades matemáticas o simplemente desees consolidar tus conocimientos, estos ejercicios te proporcionarán una sólida comprensión de cómo trabajar con fracciones y cómo aplicarlas en situaciones del mundo real.

Operaciones básicas con fracciones
Expresa cada una de las siguientes fracciones de hora en minutos:

Recordemos que  hora
hora 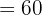 minutos. Por lo cual para convertir cada fracción en minutos se puede utilizar una regla de tres simple.
minutos. Por lo cual para convertir cada fracción en minutos se puede utilizar una regla de tres simple.
1 Conversión de
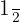 hora en minutos:
hora en minutos: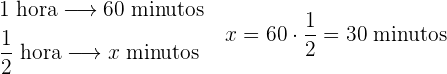
2 Conversión de
 hora en minutos:
hora en minutos: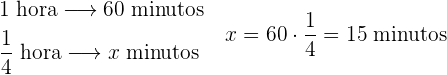
3 Conversión de
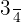 hora en minutos:
hora en minutos: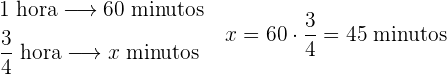
4 Conversión de
 hora en minutos:
hora en minutos: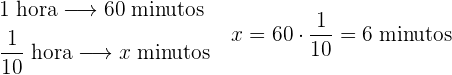
5 Conversión de
 hora en minutos:
hora en minutos: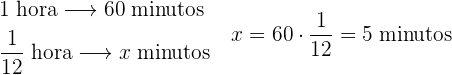
6 Conversión de
 hora en minutos:
hora en minutos: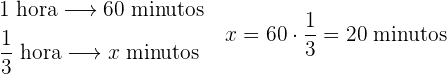
Halla los pares de fracciones equivalentes y colócalas en parejas:
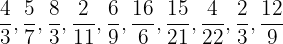
Para resolver este ejercicio, por practicidad utilizaremos la reducción de fracciones. Así notemos que las fracciones:
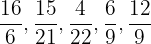 son reducibles.
son reducibles.
1 Reducimos la fracción 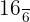 :
:
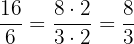
Por tanto el par equivalente de la fracción 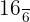 es
es 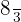 .
.
2 Reducimos la fracción 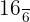 :
:
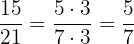
Por tanto el par equivalente de la fracción 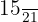 es
es 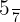 .
.
3 Reducimos la fracción 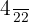 :
:
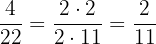
Por tanto el par equivalente de la fracción 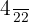 es
es 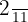 .
.
4Reducimos la fracción  :
:
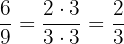
Por tanto el par equivalente de la fracción  es
es 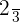 .
.
5Reducimos la fracción 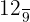 :
:
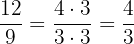
Por tanto el par equivalente de la fracción 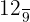 es
es 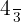 .
.
Escribe los inversos de:
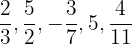
Primero, recordemos que un número y su inverso satisfacen que su producto es igual a 1.
1 El inverso  de
de 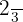 debe satisfacer que
debe satisfacer que 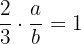 , por lo tanto
, por lo tanto 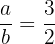 .
.
2 El inverso  de
de 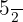 debe satisfacer que
debe satisfacer que 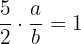 , por lo tanto
, por lo tanto 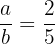 .
.
3 El inverso  de
de 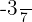 debe satisfacer que
debe satisfacer que 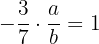 , por lo tanto
, por lo tanto 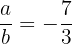 .
.
4 El inverso  de
de 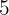 debe satisfacer que
debe satisfacer que 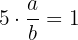 , por lo tanto
, por lo tanto 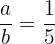 .
.
5 El inverso  de
de 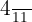 debe satisfacer que
debe satisfacer que 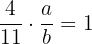 , por lo tanto
, por lo tanto 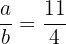 .
.
Compara las fracciones dadas y escribe el signo "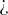 " o "
" o "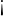 " donde corresponda.
" donde corresponda.
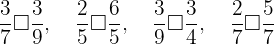
Para resolver este ejercicio, utilizaremos los siguientes dos resultados:
- De dos fracciones que tienen el mismo numerador es menor el que tiene mayor denominador.
- De dos fracciones que tienen el mismo denominador es menor la que tiene menor numerador.
De tal manera que de lo anterior se sigue:
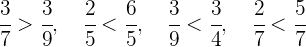
Compara las siguientes fracciones:
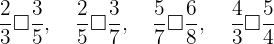
Para resolver este ejercicio necesitamos calcular el común denominador de cada una de las fracciones que se están comparando. Recordemos que será menor la de numerador más pequeño. Así bien tenemos lo siguiente:
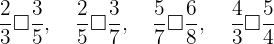
Calculando un común denominador para cada uno de los casos tenemos lo siguiente:
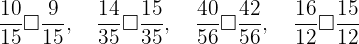
Por lo tanto se satisfacen las siguientes desigualdades:
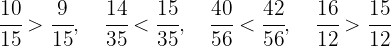
Es decir:
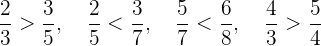
Ordenar de menor o mayor:
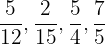
En primer lugar tenemos que calcular el m.c.m.de los denominadores para poder poner las fracciones a común denominador, es menor la que tiene menor numerador.
El mínimo común múltiplo 60, nos indica que es un número que divide a cada uno de los denominadores. Reescribimos cada una de las fracciones, de tal manera que obtengamos una fracción equivalente a las iniciales pero con denominador 60:
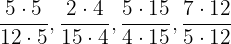
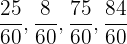
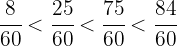
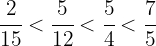
Desarrolla de dos formas distintas la siguiente operación:
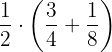
1 Aplicando primero la propiedad distributiva:
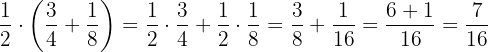
2 Desarrollando primero la suma:
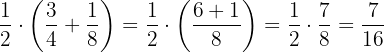
Calcula el resultado de cada una de las sumas, apoyándote en la factorización del factor común.
a 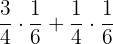
b 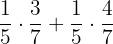
Factorizar es el proceso inverso a la propiedad distributiva, podemos transformar la suma en producto extrayendo dicho factor, es decir:
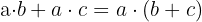
a Para calcular 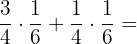 factorizamos
factorizamos 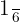 y después resolvemos:
y después resolvemos:
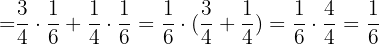
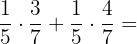 factorizamos
factorizamos  y después resolvemos:
y después resolvemos:
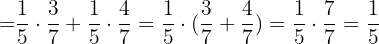
Clasifica las siguientes fracciones en propias o impropias:
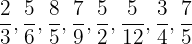
Para responder recordemos dos cosas:
- En las fracciones propias el denominador es mayor que el numerador.
- En las fracciones impropias el denominador es menor que el numerador.
1 Fracciones propias:
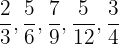
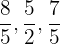
Calcula la suma de las siguientes fracciones:
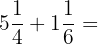
Reescribimos y desarrollamos la suma:
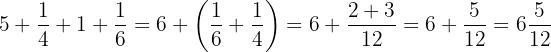
Conversiones de expresiones decimales a fracciones
Convertir en fracción las siguientes expresiones decimales:

1 Conversión en fracción de 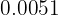 :
:
- Al ser un número decimal exacto en el numerador escribimos el número sin la coma y en denominador la unidad seguida de 4 ceros porque hay 4 cifras decimales, como se muestra a continuación:
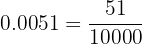
2 Conversión en fracción de 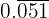 :
:
- Al ser un número periódico puro en el numerador escribimos el número sin la coma y en denominador 3 nueves porque hay 3 cifras periódicas:
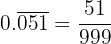 .
.
3 Conversión en fracción de  :
:
- Al ser un número periódico mixto en el numerador escribimos el número sin la coma y restamos la parte que queda fuera del periodo. En denominador hay un nueve y dos ceros porque tenemos una cifra en el período y hay dos cifras decimales:
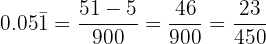
Convierte en fracción las siguientes expresiones decimales:
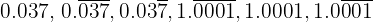
1 Conversión a fracción de 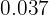 :
:
2 Conversión a fracción de 3 Conversión a fracción de 4 Conversión a fracción de 5 Conversión a fracción de 6 Conversión a fracción de 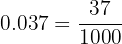
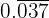 :
: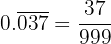
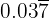 :
: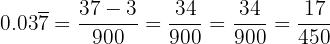
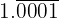 :
: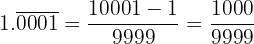
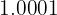 :
: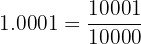
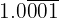 :
: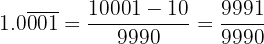
Operaciones con fracciones y decimales periódicos
Realizar las siguientes operaciones:
a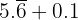
b
a Para calcular la suma de 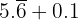 .
.
Primero, convertiremos en fracción ambas expresiones decimales y luego desarrollaremos la suma:
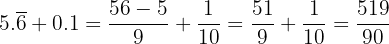
b Para calcular 
Primero, convertiremos en fracción ambas expresiones decimales y luego desarrollaremos la razón:
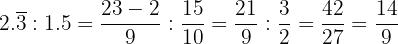
Resuelve las siguientes operaciones con fracciones:
a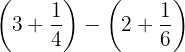
b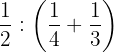
c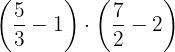
d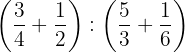
a Resolvemos 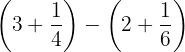 :
:
Quitamos paréntesis, en el 2º como tenemos el signo menos delante tomamos el opuesto, es decir, que cambiamos todo de signo.
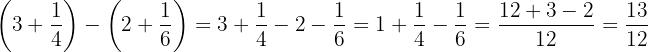
bResolvemos 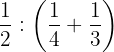
En primer lugar efectuamos la suma del interior del paréntesis, posteriormente dividimos las fracciones y por último simplificamos.
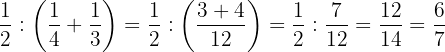
cResolvemos 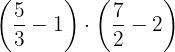
- Realizamos las operaciones de los paréntesis, efectuamos el producto de los resultados y simplificamos
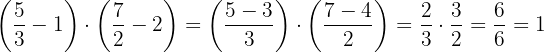
dResolvemos  :
:
- Realizamos las operaciones de los paréntesis, efectuamos la división de los resultados y simplificamos.
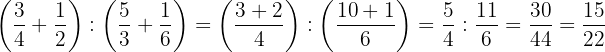
Efectúa las siguientes divisiones:
a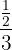
b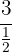
c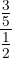
Para resolver cada una de las divisiones recordemos que se multiplican los valores extremos (arriba y abajo) el producto es el numerador, mientras que el producto de los valores internos es el denominador. De tal manera que obtenemos los siguientes resultados:
a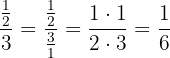
b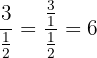
c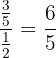
Realiza las operaciones correspondientes:
a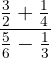
b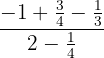
aPara calcular la suma de 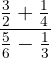 , primero:
, primero:
- Realizamos las operaciones en el numerador y denominador.
- La fracción resultante la ponemos como un división de dos fracciones, simplificamos, realizamos la división y volvemos a simplificar.
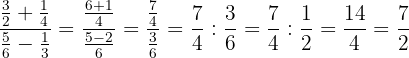
bPara realizar la suma de 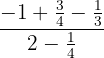 :
:
- Operamos igual que el ejercicio anterior:
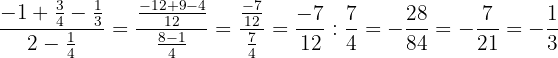 .
.
Efectúa esta operación:
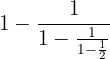
1En primer lugar efectuamos 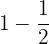
2Hacemos el inverso de 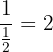 , de tal manera que obtenemos lo que se muestra a continuación:
, de tal manera que obtenemos lo que se muestra a continuación:
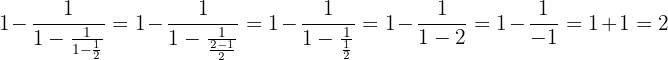
Realiza las siguientes operaciones con potencias:
a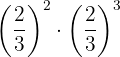
b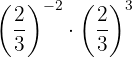
c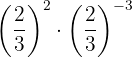
d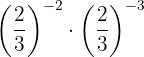
e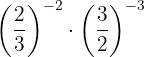
f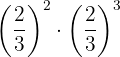
g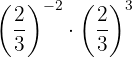
h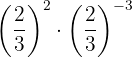
i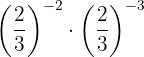
j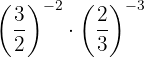
k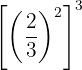
l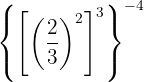
m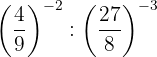
aUtilizamos que tenemos la misma base y sumamos las potencias:
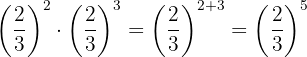
bUsamos que tenemos la misma base y restamos las potencias:
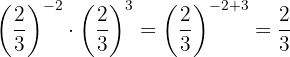
cUsamos que tenemos la misma base y restamos las potencias:
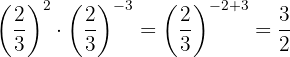
dUsamos que tenemos la misma base y restamos las potencias:
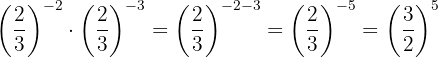
eRealizamos el siguiente procedimiento:
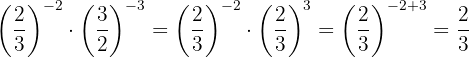
fNecesitamos dividir potencias con la misma base restamos los exponentes:
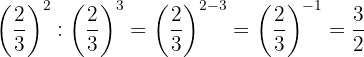
gHacemos un procedimiento similar al anterior:
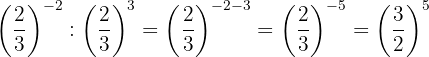
hHacemos un procedimiento similar al anterior:
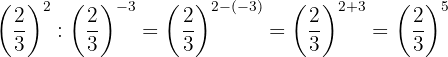
iHacemos un procedimiento similar al anterior:
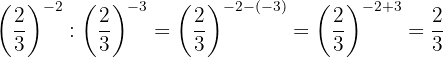
jHacemos un procedimiento similar al anterior:
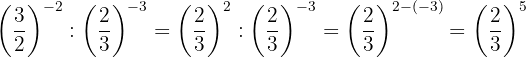
kRecordemos que para multiplicar potencias con la misma base se multiplican los exponentes:
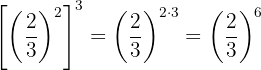
lAplicamos un procedimiento similar al ejercicio anterior, considerando al final la fracción inversa para cambiar el signo del exponente de la fracción a positivo:
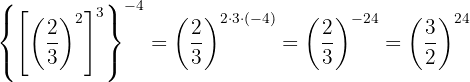
mDescomponemos los números en factores, dentro de cada paréntesis dividimos potencias con el mismo exponente, por tanto dividimos las bases y dejamos el mismo exponente, de la siguiente manera:
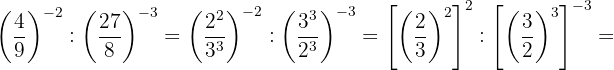
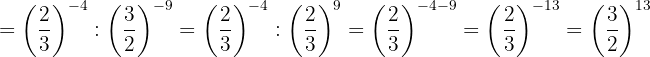
Efectúa:
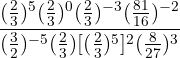
1Trataremos de poner todas las fracciones con el mismo numerador y denominador, para ello descomponemos en factores los números que no sean primos
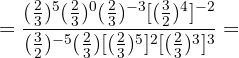
2Para pasar de una potencia con exponente negativo a exponente positivo tenemos que hacer la inversa de la fracción 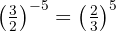 :
:
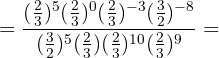
3Volvemos a poner la fracción inversa con exponente positivo 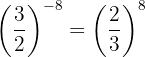 :
:
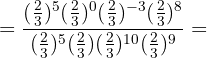
4Tanto en el numerador como en el denominador multiplicamos las potencias con la misma base y dividimos los resultados:
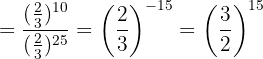
Desarrolla la siguiente operación:
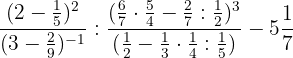
1Realizamos las operaciones indicadas en los paréntesis, en el paréntesis del 2º denominador tenemos que multiplicar primero y en siguiente paso dividimos. $5 \frac{1}{7}$ es un número mixto por tanto dejamos el mismo denominador (7) y el numerador es la suma de la multiplicación del entero (5) por el denominador (7) más el numerador del número mixto (1).
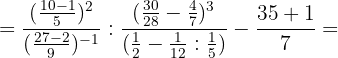
2Efectuamos las operaciones indicadas y simplificamos 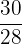 :
:
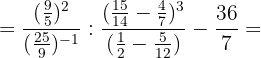
3Realizamos las operaciones indicadas y reducimos a común denominador en la 2ª fracción:
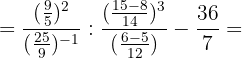
4Efectuamos la operaciones en la segunda fracción y simplificamos:
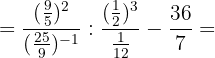
5Realizamos la potencias y tenemos en cuenta que en una fracción elevada a un número negativo tenemos que cambiar el numerador por el denominador y posteriormente elevar al exponente:
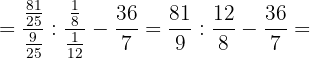
6Simplificamos y operamos:
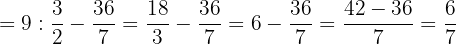
Resuelve:
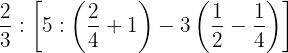
1Efectuamos las operaciones en los dos paréntesis:
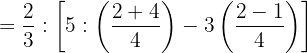
2Como hemos quitado los paréntesis el corchete se convierte en paréntesis:
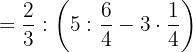
3Realizamos la división y multiplicación del paréntesis y simplificamos los resultados:
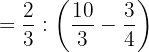
4Dividimos 2/3 por el resultado del paréntesis y simplificamos
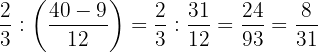
Opera:
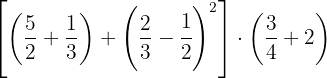
1Realizamos las operaciones en los paréntesis:
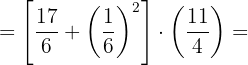
2Realizamos la potencia y sustituimos el corchete por un paréntesis
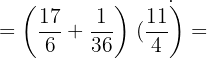
3Resolvemos el primer paréntesis
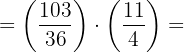
4Hacemos la multiplicación y simplificamos:
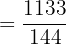
Efectúa:
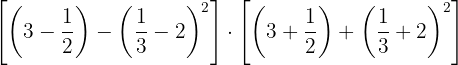
1Operamos en los paréntesis:
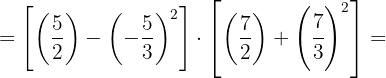
2Realizamos las potencias:
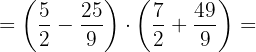
3Realizamos las operaciones del paréntesis
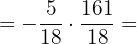
4Hacemos la multiplicación y simplificamos el resultado
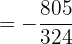
Opera:
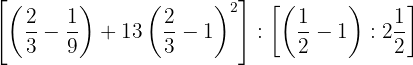
1Pasamos a fracción el número mixto 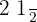 . Dejamos el mismo denominador (2) y el numerador es la suma de la multiplicación del entero (2) por el denominador (2) más el numerador del número mixto (1). Reducimos las fracciones de cada paréntesis a su común denominador.
. Dejamos el mismo denominador (2) y el numerador es la suma de la multiplicación del entero (2) por el denominador (2) más el numerador del número mixto (1). Reducimos las fracciones de cada paréntesis a su común denominador.
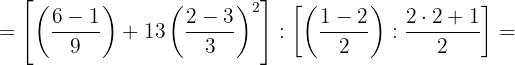
2Realizamos las operaciones en los numeradores, como dentro del 2º corchete quitamos los paréntesis, el corchete se convierte en paréntesis:
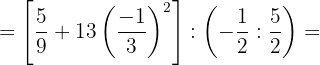
3Realizamos la potencia y como no quedan paréntesis en el primer corchete, sustituimos este por un paréntesis
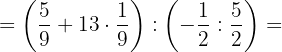
4Multiplicamos en el primer paréntesis y dividimos en el 2º
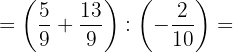
5Hacemos la suma del primer paréntesis, simplificamos en el 2º y dividimos:
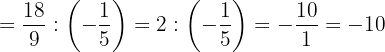
Efectúa:
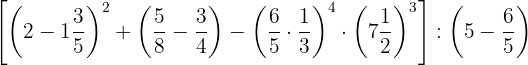
1Primero operamos con las productos y números mixtos de los paréntesis:
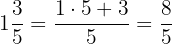
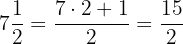
2Sustituimos los resultados:
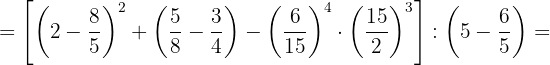
3Operamos en el primer paréntesis, quitamos el segundo, simplificamos en el tercero y operamos en el último:
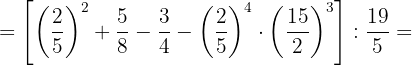
4Realizamos el producto y lo simplificamos, cambiamos el corchete por un paréntesis
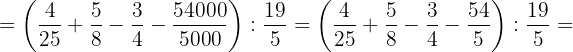
5Realizamos las operaciones del paréntesis
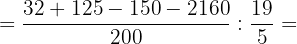
6Hacemos las operaciones del numerador, dividimos y simplificamos el resultado
Resumir con IA:














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Si van a poner ejercicio pónganlo bien si van a poner división póngame en el signo de división si van a poner multiplicación ponga bien el signo de multiplicación
Fracciónes y la unidad que representan problemas de la vida diaria usando las fracciones y las unidades que representan
La mitad y la mitad
En otro problema podemos ver qué está fracciones y litros ahí podemos ver los litros de agua y que tienes que saber cuántos litros de agua quedan
Por lo tanto quedan 90 litros de agua en el tanque
Hola, muchas gracias por tu aportación.
Hola lamentamos los errores cometidos, podrías hacernos el favor de mencionarnos donde están las fallas para poder corregirlas.
En el ejercicio dos no da esa respuesta
Hola el artículo que revise hay varios ejercicios 2, pero no encontré el error que mencionas, podrías dar mas detalles por favor, así se podrá corregir.