Capítulos
¡Bienvenidos al apasionante mundo de las fracciones! Si alguna vez has encontrado desafiantes los problemas matemáticos que involucran estas pequeñas partes de un todo, has llegado al lugar adecuado. En esta página dedicada a problemas sobre fracciones, exploraremos un sinfín de situaciones en las que estas numéricas piezas se convierten en la clave para resolver acertijos y situaciones del mundo real.
Nuestro equipo de entusiastas de las matemáticas te guiará a través de problemas prácticos y desafiantes, desmitificando el mundo de las fracciones y mostrándote cómo aplicar estas habilidades en tu vida cotidiana.
Así que, si estás listo para sumergirte en el emocionante universo de las fracciones y desbloquear su poder para resolver problemas, esta página es para ti. ¡Prepárate para explorar la magia detrás de los números fraccionarios y llevar tus habilidades matemáticas a un nivel superior! ¡Comencemos a resolver problemas con fracciones juntos!

Fracciones y las unidades que representan
Calcula qué fracción de la unidad representan:
a La mitad de la mitad.
b La mitad de la tercera parte.
c La tercera parte de la mitad.
d La mitad de la cuarta parte.
e La cuarta parte de la mitad.
a La mitad de la mitad.
La mitad de un número  se escribe como
se escribe como
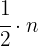
Como el número  es una mitad, entonces obtenemos
es una mitad, entonces obtenemos
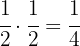
b La mitad de la tercera parte.
La mitad de un número  se escribe como
se escribe como
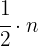
Como el número  es una tercera parte, entonces obtenemos
es una tercera parte, entonces obtenemos

c La tercera parte de la mitad.
La tercera parte de un número  se escribe como
se escribe como
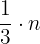
Como el número  es una mitad, entonces obtenemos
es una mitad, entonces obtenemos

d La mitad de la cuarta parte.
La mitad de un número  se escribe como
se escribe como

Como el número  es una cuarta parte, entonces obtenemos
es una cuarta parte, entonces obtenemos

e La cuarta parte de la mitad.
La cuarta parte de un número  se escribe como
se escribe como
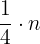
Como el número  es una mitad, entonces obtenemos
es una mitad, entonces obtenemos
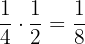
Problemas de la vida diaria usando fracciones
Para preparar un pastel, se necesita: 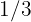 de un paquete de
de un paquete de 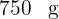 de azúcar,
de azúcar, 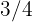 de un paquete de harina de kilo y
de un paquete de harina de kilo y 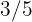 de una barra de mantequilla de
de una barra de mantequilla de  . Halla, en gramos, las cantidades que se necesitan para preparar el pastel.
. Halla, en gramos, las cantidades que se necesitan para preparar el pastel.
Escribimos en gramos cada una de las cantidades que se necesitan para preparar el pastel.
 de un paquete de
de un paquete de 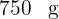 de azúcar
de azúcar
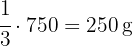
 de un paquete de harina de kilo
de un paquete de harina de kilo
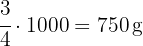
 de una barra de mantequilla de
de una barra de mantequilla de 
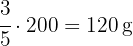
De una pieza de tela de  se cortan
se cortan 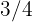 . ¿Cuántos metros mide el trozo restante?
. ¿Cuántos metros mide el trozo restante?
Calculamos a cuántos metros equivalen 
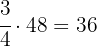 .
.
Se lo restamos a los  .
.
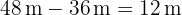 .
.
Una caja contiene  bombones. Eva se comió
bombones. Eva se comió 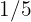 de los bombones y Ana
de los bombones y Ana  .
.
a¿Cuántos bombones comió Eva y cuántos Ana?
b¿Qué fracción de bombones se comieron entre las dos?
a¿Cuántos bombones comió Eva y cuántos Ana?
Multiplicamos  por la fracción correspondiente de Eva y Ana.
por la fracción correspondiente de Eva y Ana.
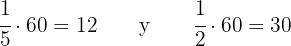
Eva ha comido  y Ana
y Ana  .
.
b¿Qué fracción de bombones se comieron entre las dos
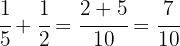
Hace unos años Pedro tenía  años, que representan los
años, que representan los  de su edad actual. ¿Qué edad tiene Pedro?
de su edad actual. ¿Qué edad tiene Pedro?
Representamos en forma gráfica
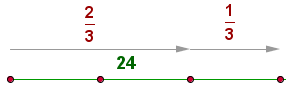
 equivale a dos de las tres partes de la edad, entonces calculamos cuánto vale una parte (24:2) y el resultado se multiplica por el número total de partes, o sea,
equivale a dos de las tres partes de la edad, entonces calculamos cuánto vale una parte (24:2) y el resultado se multiplica por el número total de partes, o sea,  .
.
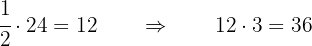
Por lo tanto, Pedro tiene  años de edad.
años de edad.
Los  de los ingresos de una comunidad de vecinos se emplean en combustible,
de los ingresos de una comunidad de vecinos se emplean en combustible, 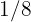 se emplea en electricidad,
se emplea en electricidad, 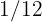 en la recogida de basuras,
en la recogida de basuras, 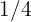 en mantenimiento del edificio y el resto se emplea en limpieza.
en mantenimiento del edificio y el resto se emplea en limpieza.
a ¿Qué fracción de los ingresos se emplea en limpieza?
b De acuerdo con la fracción de ingresos empleada, ordena las partidas enumeradas de menor a mayor.
a¿Qué fracción de los ingresos se emplea en limpieza?
Para resolver esto, debemos sumar las fracciones de cada una de las demás partidas este resultado restarlo a  . Así
. Así
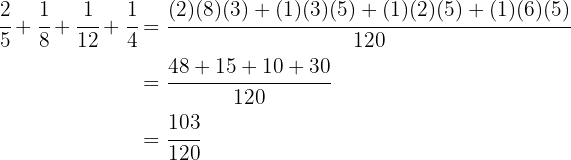
Restando nuestro resultado anterior a  obtenemos
obtenemos
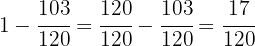
Por lo tanto, se emplearon 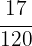 del ingreso a limpieza.
del ingreso a limpieza.
bDe acuerdo con la fracción de ingresos empleada, ordena las partidas enumeradas de menor a mayor
 \displaystyle \cfrac{1}{12} < \cfrac{1}{8} < \cfrac{17}{120} < \cfrac{1}{4} < \cfrac{2}{5} [/latex]
\displaystyle \cfrac{1}{12} < \cfrac{1}{8} < \cfrac{17}{120} < \cfrac{1}{4} < \cfrac{2}{5} [/latex]
Tomamos las fracciones con el mismo denominador
 \displaystyle \cfrac{10}{120} < \cfrac{15}{120} < \cfrac{17}{120} < \cfrac{30}{120} < \cfrac{48}{120}[/latex]
\displaystyle \cfrac{10}{120} < \cfrac{15}{120} < \cfrac{17}{120} < \cfrac{30}{120} < \cfrac{48}{120}[/latex]
En las elecciones locales celebradas en un pueblo, 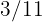 de los votos fueron para el partido
de los votos fueron para el partido  ,
, 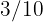 para el partido
para el partido  ,
, 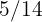 para
para  y el resto para el partido
y el resto para el partido  . El total de votos ha sido de
. El total de votos ha sido de  . Calcular:
. Calcular:
a El número de votos obtenidos por cada partido.
b El número de abstenciones sabiendo que el número de votantes representa 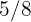 del censo electoral.
del censo electoral.
aEl número de votos obtenidos por cada partido.
Partido A:
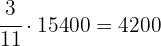
Partido B:
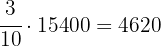
Partido C:
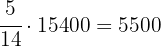
Partido D:
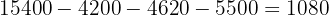
bEl número de abstenciones sabiendo que el número de votantes representa  del censo electoral.
del censo electoral.
Notemos que el total de votantes es  , es decir, que es
, es decir, que es  , por lo tanto, la fracción de abstenciones es
, por lo tanto, la fracción de abstenciones es
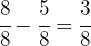
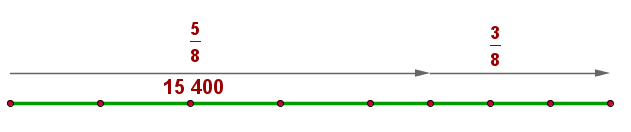
Así, la cantidad de abstenciones usando regla de tres está dada por
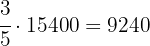
La recta está dividida en  partes iguales para saber la cantidad que representa cada parte tenemos en cuenta que las
partes iguales para saber la cantidad que representa cada parte tenemos en cuenta que las  primeras partes (la de los votos) suman
primeras partes (la de los votos) suman  por tanto una parte será
por tanto una parte será 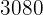 multiplicado por
multiplicado por  que es igual a
que es igual a  . Y las otras tres partes (la de las abtenciones) se obtendrán multiplicando
. Y las otras tres partes (la de las abtenciones) se obtendrán multiplicando  por
por 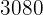 .
.
Jorge gana 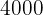 € al mes y destina las siguientes fracciones de su sueldo a los siguientes apartados.
€ al mes y destina las siguientes fracciones de su sueldo a los siguientes apartados. 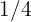 en alquiler,
en alquiler, 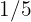 en comida,
en comida, 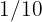 en gasolina,
en gasolina, 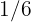 en servicios del hogar y ropa, y
en servicios del hogar y ropa, y 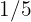 en gastos personales. Si Jorge ahorra lo restante
en gastos personales. Si Jorge ahorra lo restante
a ¿Qué fracción ahorra Jorge?
b ¿A cuánto corresponde esta fracción en dinero?
a¿Qué fracción ahorra Jorge?
Para resolver esto, debemos sumar cada fracción y el resultado restarlo a  . Así
. Así
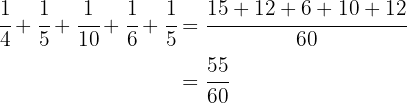
Restando nuestro resultado anterior a  obtenemos
obtenemos
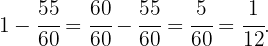
Por lo tanto, Jorge ahorra 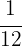 de su ingreso mensual.
de su ingreso mensual.
b¿A cuánto corresponde esta fracción en dinero?
Para saber a cuánto corresponde en dinero esta fracción, la multiplicamos por el total de ingresos
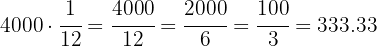
Así, Jorge ahorra aproximadamente 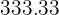 € al mes.
€ al mes.
La materia de historia se calificará de acuerdo a los siguientes rubros: 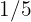 examen,
examen, 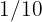 participación,
participación, 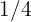 tareas,
tareas, 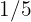 proyecto,
proyecto, 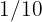 puntualidad y el resto en asistencia. ¿Qué fracción represanta la asistencia del total de la calificación?
puntualidad y el resto en asistencia. ¿Qué fracción represanta la asistencia del total de la calificación?
Para resolver esto, debemos sumar cada fracción y el resultado restarlo a  . Así
. Así
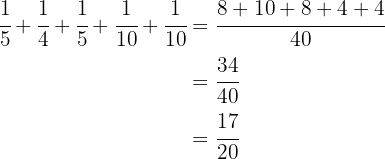
Restando nuestro resultado anterior a  obtenemos
obtenemos
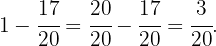
Por lo tanto, 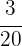 corresponde a la asistencia.
corresponde a la asistencia.
Un campesino siembra todos los años su terreno de  héctarea con las siguientes proporciones:
héctarea con las siguientes proporciones: 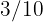 de trigo,
de trigo, 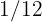 de frijol,
de frijol, 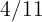 de cebada, y el resto con maíz. ¿Qué fracción de terreno deberá ser sembrada con maíz?
de cebada, y el resto con maíz. ¿Qué fracción de terreno deberá ser sembrada con maíz?
Para resolver esto, debemos sumar las fracciones y el resultado restarlo a  . Así
. Así

Restando nuestro resultado anterior a  obtenemos
obtenemos
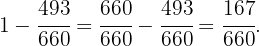
Por lo tanto, 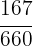 de terreno será sembrado con maíz.
de terreno será sembrado con maíz.
Fabiola planea leer un libro de 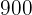 páginas que compró la semana pasada. Dado que tiene distintas actividades a la semana, ella planea leer un promedio de
páginas que compró la semana pasada. Dado que tiene distintas actividades a la semana, ella planea leer un promedio de  páginas todos los días de lunes a viernes, y el sábado y domingo,
páginas todos los días de lunes a viernes, y el sábado y domingo,  páginas cada día.
páginas cada día.
a ¿Qué fracción del total representa las páginas que Fabiola puede leer cada día de la semana?
b ¿En cuánto tiempo leerá el libro?
a¿Qué fracción del total representa las páginas que Fabiola puede leer cada día de la semana?
Sea  la fracción de páginas que Fabiola puede leer de lunes a viernes. Así, se tiene la siguiente relación:
la fracción de páginas que Fabiola puede leer de lunes a viernes. Así, se tiene la siguiente relación:
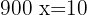
Resolvemos para 
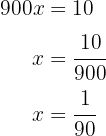
Por lo tanto, cada día de lunes a viernes, Fabiola lee 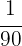 del total de páginas del libro.
del total de páginas del libro.
Similarmente para el sábado y domingo, se tiene la relación
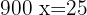
Resolviendo
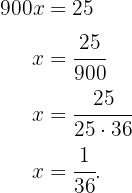
Así, tanto el sádado como el domingo, Fabiola lee 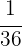 del total de páginas del libro.
del total de páginas del libro.
b¿En cuánto tiempo leerá el libro?
Ya que, cada día de lunes a viernes, Fabiola lee  páginas, entonces en estos
páginas, entonces en estos  días ella leerá
días ella leerá  páginas. De igual manera, el sábado y domingo, Fabiola lee
páginas. De igual manera, el sábado y domingo, Fabiola lee  páginas. Así, cada semana ella leerá
páginas. Así, cada semana ella leerá  páginas. Por lo tanto, ella tardará
páginas. Por lo tanto, ella tardará  semanas en leer el libro.
semanas en leer el libro.
Fracciones y litros
Un depósito contiene 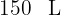 de agua. Se consumen los
de agua. Se consumen los  de su contenido. ¿Cuántos litros de agua quedan?
de su contenido. ¿Cuántos litros de agua quedan?
El contenido total de agua es 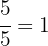 y consumimos
y consumimos  , por tanto queda:
, por tanto queda:
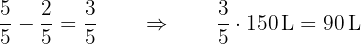
Una familia ha consumido en un día de verano: Dos botellas de litro y medio de agua, cuatro botes de 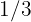 de litro de zumo y cinco limonadas de
de litro de zumo y cinco limonadas de 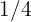 de litro. ¿Cuántos litros de líquido han bebido? Expresa el resultado con un número mixto.
de litro. ¿Cuántos litros de líquido han bebido? Expresa el resultado con un número mixto.
En primer lugar pasamos el litro y medio a fracción.

Multiplicamos cada número de elementos por su fracción correspondiente. Ponemos a común denominador y sumamos
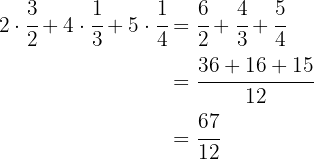
Se divide el numerador por el denominador  , el cociente
, el cociente  es el entero del número mixto, el resto
es el entero del número mixto, el resto  es el numerador de la fracción y el denominador es el mismo de la fracción impropia
es el numerador de la fracción y el denominador es el mismo de la fracción impropia  :
:
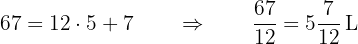
¿Cuántos tercios de litro hay en  ?
?
Dividimos el total de litros entre un tercio

También lo podemos resolver empleando gráficos
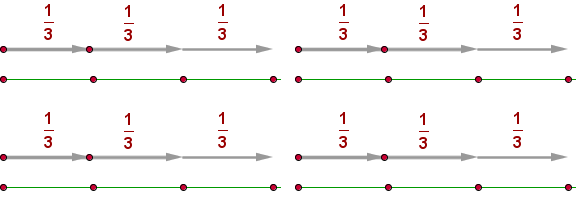
En  hay tres tercios, por lo que en
hay tres tercios, por lo que en  habrá:
habrá: 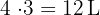
El litro de gasolina se vende en  pesos. Si el tanque de un automóvil se llena con
pesos. Si el tanque de un automóvil se llena con  pesos. ¿Cuántos litros representa esta cantidad?
pesos. ¿Cuántos litros representa esta cantidad?
Convertiremos los  pesos a litros con la equivalencia de
pesos a litros con la equivalencia de  litro cuesta
litro cuesta  pesos. Note que
pesos. Note que
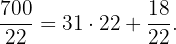
Así,
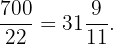
Es decir, por  pesos nos darían
pesos nos darían 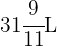 de gasolina.
de gasolina.
Una planta en una maceta es regada cada  días con
días con  litros de agua. La planta consume
litros de agua. La planta consume 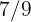 del agua que recibe y el resto es desechada por el desagüe de la maceta. Si la planta es regada durante
del agua que recibe y el resto es desechada por el desagüe de la maceta. Si la planta es regada durante  días. ¿Cuánta agua fue consumida y cuánta fue desechada por la planta?
días. ¿Cuánta agua fue consumida y cuánta fue desechada por la planta?
Para resolver esto, observamos que, en el periodo de  días, la planta fue regada
días, la planta fue regada  veces. Si cada vez la planta recibio
veces. Si cada vez la planta recibio  de agua, entonces en este periodo, la planta recibió
de agua, entonces en este periodo, la planta recibió 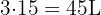 de agua.
de agua.
Multiplicamos esta cantidad por  para conocer la cantidad de agua que fue consumida por la planta. Así,
para conocer la cantidad de agua que fue consumida por la planta. Así,

Así, la planta consumió 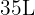 de agua.
de agua.
Similarmente, multiplicamos los  por
por  que es la cantidad de agua que la planta desecha. Entonces,
que es la cantidad de agua que la planta desecha. Entonces,
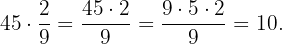
Es decir, la planta desechó  de agua en este periodo de tiempo.
de agua en este periodo de tiempo.
Fracciones y distancias
Un cable de  de longitud se corta en dos trozos. Uno tiene las
de longitud se corta en dos trozos. Uno tiene las 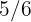 partes del cable. ¿Cuántos metros mide cada trozo?
partes del cable. ¿Cuántos metros mide cada trozo?
Calculamos a cuántos metros equivalen  y se lo restamos a
y se lo restamos a  .
.
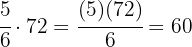
Restando a 
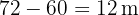
Ana ha recorrido 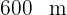 , que son los
, que son los 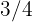 del camino de su casa al instituto. ¿Qué distancia hay de su casa al instituto?
del camino de su casa al instituto. ¿Qué distancia hay de su casa al instituto?
Representamos en forma gráfica
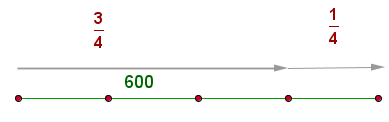
 equivale a las tres partes del camino, entonces calculamos cuánto vale una parte
equivale a las tres partes del camino, entonces calculamos cuánto vale una parte  y el resultado se multplica por el número total de partes
y el resultado se multplica por el número total de partes  :
:
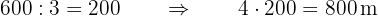
Dos automóviles  y
y  hacen un mismo trayecto de
hacen un mismo trayecto de  . El automóvil
. El automóvil  lleva recorrido los
lleva recorrido los 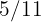 del trayecto cuando el
del trayecto cuando el  ha recorrido los
ha recorrido los 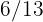 del mismo. ¿Cuál de los dos va primero? ¿Cuántos kilómetros llevan recorridos cada uno?
del mismo. ¿Cuál de los dos va primero? ¿Cuántos kilómetros llevan recorridos cada uno?
Reducimos a común denominador para poder comparar las fracciones
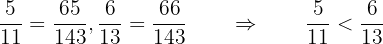
El automovil  va primero.
va primero.
Ahora analicemos ahora la distancia recorrida por cada uno:
Automovil 
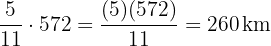
Automovil 
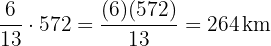
Un sastre tiene  metros y necesita
metros y necesita 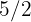 metros de tela para hacer un pantalón. ¿Qué cantidad de tela necesita comprar para hacer el pantalón?
metros de tela para hacer un pantalón. ¿Qué cantidad de tela necesita comprar para hacer el pantalón?
Para resolver este problema, necesitamos restarle a la fracción  , que es la tela que se necesita, la fracción
, que es la tela que se necesita, la fracción  , que es la tela que tiene el sastre. El resultado será la cantidad que se necesita. Así,
, que es la tela que tiene el sastre. El resultado será la cantidad que se necesita. Así,

Por lo tanto, el sastre necesita comprar 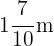 de tela.
de tela.
Un tractor trabaja  metros de tierra en
metros de tierra en  de hora. ¿Cuántos kilómetros de tierra trabajará en
de hora. ¿Cuántos kilómetros de tierra trabajará en 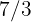 horas?
horas?
Calculamos cuantos  de hora hay en los
de hora hay en los  de hora. Para hacer esto, hacemos
de hora. Para hacer esto, hacemos
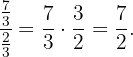
Finalmente, multiplicamos  por
por  y simplificamos
y simplificamos
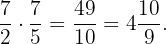
Por lo tanto, el tractor trabajará 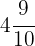 kilómetros en este tiempo.
kilómetros en este tiempo.
Fracciones y dinero
Elena va de compras con 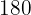 euros. Se gasta
euros. Se gasta 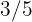 de esa cantidad. ¿Cuánto le queda?
de esa cantidad. ¿Cuánto le queda?
Calculamos a cuánto equivalen  y se lo restamos a
y se lo restamos a 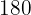 .
.
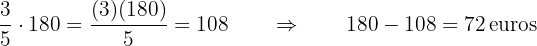 .
.
Un padre reparte entre sus hijos 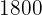 euros. Al mayor le da
euros. Al mayor le da 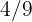 de esa cantidad, al mediano
de esa cantidad, al mediano 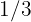 y al menor el resto. ¿Qué cantidad recibió cada uno? ¿Qué fracción del dinero recibió el tercero?
y al menor el resto. ¿Qué cantidad recibió cada uno? ¿Qué fracción del dinero recibió el tercero?
Mayor:
 .
.
Mediano:
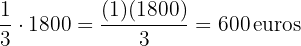 .
.
Menor:
Primero calculemos la fracción dinero correspondiente al menor
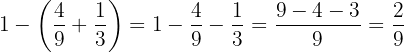 .
.
Ahora calculemos la cantidad
 .
.
Una persona tiene una deuda de  euros y pagó
euros y pagó  de ella. ¿Cuánto le falta por pagar?
de ella. ¿Cuánto le falta por pagar?
Para resolver este problema, calculamos primero la cantidad pagada y luego la restamos a  para conocer el monto que resta por pagar.
para conocer el monto que resta por pagar.
Lo pagado es
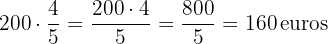 .
.
Lo que resta por pagar es
 .
.
Dos amigos, Luis y Juan, fueron de compras y entre los dos gastaron un total de  euros. Si Luis gastó
euros. Si Luis gastó  de lo que gastó Juan, ¿cuánto gastó cada quien?
de lo que gastó Juan, ¿cuánto gastó cada quien?
Sea  la cantidad gastada por Luis y
la cantidad gastada por Luis y 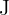 la cantidad gastada por Juan. Así, se tienen las siguientes relaciones
la cantidad gastada por Juan. Así, se tienen las siguientes relaciones
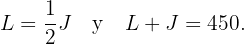 .
.
Sustituimos la primera condición en la segunda ecuación
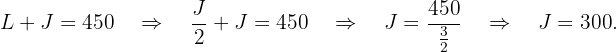 .
.
Por lo tanto, Juan pagó  euros y Luis pagó
euros y Luis pagó
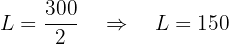
euros.
Alicia dispone de  euros para compras. El jueves gastó
euros para compras. El jueves gastó  de esa cantidad y el sábado los
de esa cantidad y el sábado los 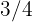 de lo que le quedaba. ¿Cuánto gastó cada día y cuánto le queda al final?
de lo que le quedaba. ¿Cuánto gastó cada día y cuánto le queda al final?
Jueves:

Sábado:
Primero calculemos lo que le quedó después del jueves
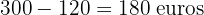
Ahora a esta cantidad hay que calcular la fracción que se gastó
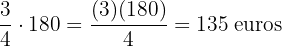
Restante:
Restemos a 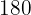 la cantidad que gastó el sábado, así
la cantidad que gastó el sábado, así

Te ayudamos a encontrar el curso matematicas que mejor se adapte a ti: ¿quieres un profesor de matematicas online? ¿o prefieres un profesor que se desplace a domicilio? En Superprof encontrarás a tu profe ideal.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Si van a poner ejercicio pónganlo bien si van a poner división póngame en el signo de división si van a poner multiplicación ponga bien el signo de multiplicación
Fracciónes y la unidad que representan problemas de la vida diaria usando las fracciones y las unidades que representan
La mitad y la mitad
En otro problema podemos ver qué está fracciones y litros ahí podemos ver los litros de agua y que tienes que saber cuántos litros de agua quedan
Por lo tanto quedan 90 litros de agua en el tanque
Hola, muchas gracias por tu aportación.
Hola lamentamos los errores cometidos, podrías hacernos el favor de mencionarnos donde están las fallas para poder corregirlas.
En el ejercicio dos no da esa respuesta
Hola el artículo que revise hay varios ejercicios 2, pero no encontré el error que mencionas, podrías dar mas detalles por favor, así se podrá corregir.