Capítulos
Las sucesiones y progresiones son herramientas fundamentales en el estudio de las matemáticas, especialmente en el análisis de patrones numéricos y el desarrollo del pensamiento lógico. Comprender cómo se comportan estas secuencias nos permite resolver problemas que involucran crecimiento, cambio constante y relaciones entre términos.
A continuación encontrarás una serie de ejercicios resueltos paso a paso, que abarcan tanto sucesiones aritméticas como geométricas, así como otros tipos de progresiones y patrones numéricos. Cada ejercicio ha sido seleccionado con el objetivo de reforzar los conceptos teóricos, mostrar métodos de resolución y ayudarte a desarrollar habilidades prácticas para enfrentar problemas similares por tu cuenta.

Término general y propiedades
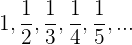
Numerador
Es constante igual a 
Denominador
Es una progresión aritmética de 
Comienza en 1 por lo que el denominador está dado por 

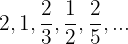
Numerador
Es constante igual a 
Denominador
Es una progresión aritmética de 
Comienza en 1 por lo que el denominador está dado por 
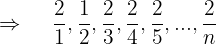

Numerador
Es una progresión aritmética con una 
Comienza en  por lo que el númerador está dado por
por lo que el númerador está dado por 
Denominador
Es una progresión aritmética de 
Comienza en  por lo que el númerador está dado por
por lo que el númerador está dado por 
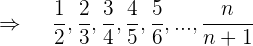

En esta sucesión se han simplificado algunas fracciones.
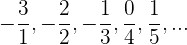
Numerador
Es una progresión aritmética con una 
Comienza en  por lo que el númerador está dado por
por lo que el númerador está dado por 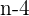
Denominador
Es una progresión aritmética de 
Comienza en  por lo que el númerador está dado por
por lo que el númerador está dado por 
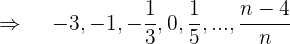

Si prescindimos del signo es una progresión aritmética con una 
Por ser los términos impares los negativos multiplicamos por 
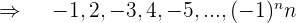
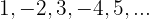
Si prescindimos del signo es una progresión aritmética con una 
Por ser los términos impares los positivos multiplicamos por 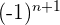
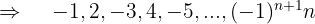

En esta sucesión se han simplificado algunas fracciones.
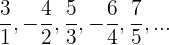
Numerador
Si prescindimos del signo, es una progresión aritmética con una 
Comienza en  por lo que el númerador está dado por
por lo que el númerador está dado por 
Denominador
Es una progresión aritmética de 
Comienza en 1 por lo que el númerador está dado por 
Por ser los términos pares los negativos multiplicamos por (–1)n+1
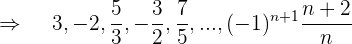
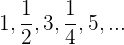

Es una sucesión oscilante
Los términos impares forman progresión aritmética con una  , si no tenemos en cuenta los términos pares
, si no tenemos en cuenta los términos pares
El denominador de los términos pares forman progresión aritmética con una 
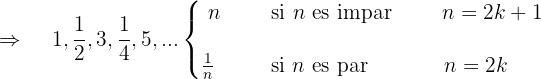
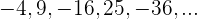
Notamos que podemos reescribir la sucesión como
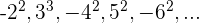
Si prescindimos del signo y del exponente tenemos una progresión aritmética con una 
Por estar los términos al cuadrado, tenemos que elevar el término general al cuadrado
Por ser los términos impares los negativos multiplicamos por 
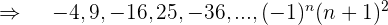
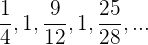
Notamos que podemos reescribir la sucesión de la siguiente manera,
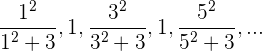
Es una sucesión oscilante
Numerador
El numerador de los términos impares forman progresión aritmética con una  , si no tenemos en cuenta los términos pares.
, si no tenemos en cuenta los términos pares.
Por estar los términos al cuadrado, tenemos que elevar el término general al cuadrado
Denominador
El primer sumando del denominador (prescindiendo del cuadrado) es una progresión aritmética de  (sin contar los términos pares)
(sin contar los términos pares)
El término general lo tenemos que elevar al cuadrado y sumarle 
Los términos pares forman una sucesión constante.
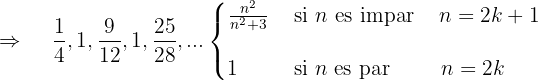
Monotonía
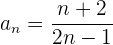
Calculamos los primero términos
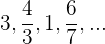
Es monótona estrictamente decreciente.
Además, si calculamos para valores muy grandes de  obtenemos
obtenemos
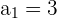
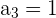

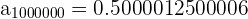
Por lo tanto, es una sucesión convergente y el límite es 0.5
Por ser decreciente, 3 es una cota superior, el máximo
0.5 es una cota inferior, el ínfimo o extremo inferior
Por tanto la sucesión está acotada
 $$0.5 < a_n \leq 3$$[/latex]
$$0.5 < a_n \leq 3$$[/latex]
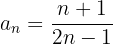
Calculamos los primero términos
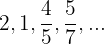
Es monótona estrictamente decreciente.
Además, si calculamos para valores muy grandes de  obtenemos
obtenemos
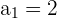
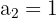
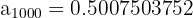
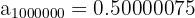
Por lo tanto, es una sucesión convergente y el límite es 0.5
Por ser decreciente, 2 es una cota superior, el máximo
0.5 es una cota inferior, el ínfimo o extremo inferior
Por tanto la sucesión está acotada
 $$0.5 < a_n \leq 2$$[/latex]
$$0.5 < a_n \leq 2$$[/latex]

Calculamos los primeros términos

No es monótona
No es convergente ni divergente
No está acotada
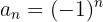
Calculamos los primeros términos
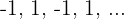
No es monótona
No es convergente ni divergente
Si está acotada
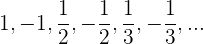
No es monótona
Es convergente porque el límite = 0
Está acotada superiormente, 1 es el máximo
Está acotada inferiormente, –1 es el mínimo
Está acotada
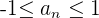
Encuentra la progresión
El cuarto término de una progresión aritmética es 10 , y el sexto es 16. Escribir la progresión.
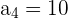

Usando la fórmula
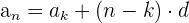
Podemos calcular

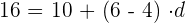
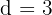
Usando la misma fórmula podemos calcular el primer término de la sucesión


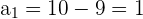
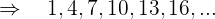
El quinto término de una progresión aritmética es 14 , y el sexto es 26. Escribir la progresión.
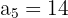
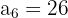
Usando la fórmula
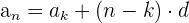
Podemos calcular

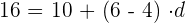
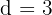
Usando la misma fórmula podemos calcular el primer término de la sucesión


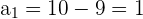
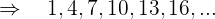
El segundo término de una progresión geométrica es 6 , y el quinto es 48. Escribir la progresión
Los términos que sabemos son
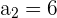
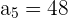
Usando la fórmula

Podemos calcular 
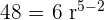
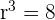

Usando la misma fórmula calculamos el primer término
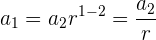
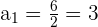

El tercer término de una progresión geométrica es 6 , y el quinto es 48. Escribir la progresión
Los términos que sabemos son
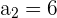
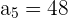
Usando la fórmula

Podemos calcular 
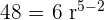
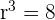

Usando la misma fórmula calculamos el primer término
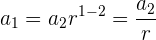
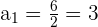

El cuarto término de una progresión geométrica es 6 , y el quinto es 48. Escribir la progresión
Los términos que sabemos son
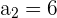
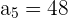
Usando la fórmula

Podemos calcular 
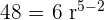
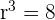

Usando la misma fórmula calculamos el primer término
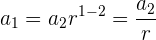
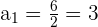

Encuentra la suma, diferencia o producto de términos
Hallar la suma de los quince primeros múltiplos de 5
Me interesa obtener la suma de los primeros quince términos de la sucesión
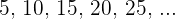
Los datos que tenemos son
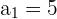
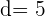
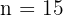
Obtenemos el término quince usando la siguiente fórmula


Usando la fórmula
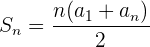
Podemos obtener la suma de los primeros  términos
términos
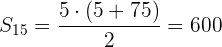
Hallar la suma de los quince primeros números acabados en 
Me interesa obtener la suma de los primeros quince términos de la sucesión

Los datos que tenemos son
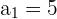

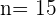
Obtenemos el término quince usando la siguiente fórmula


Con la fórmula
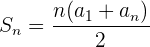
Podemos obtener la suma de los primeros
 términos
términos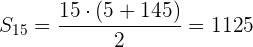
Hallar la suma de los quince primeros números pares mayores que 
Me interesa obtener la suma de los primeros quince términos de la sucesión
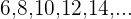
Los datos que tenemos son
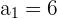

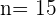
Obtenemos el término quince usando la siguiente fórmula

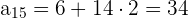
Con la fórmula
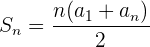
Podemos obtener la suma de los primeros
 términos
términos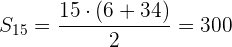
El primer término de una progresión aritmética es 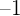 , y el décimoquinto es
, y el décimoquinto es  . Hallar la diferencia y la suma de los quince primeros términos.
. Hallar la diferencia y la suma de los quince primeros términos.
Los datos que tenemos son
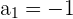
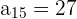
Usando la fórmula

Podemos obtener el valor de




Con la fórmula
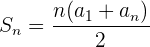
Podemos obtener la suma de los primeros
 términos
términos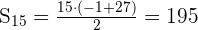
El primer término de una progresión geométrica es  , y el octavo es
, y el octavo es 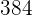 . Hallar la razón, y la suma y el producto de los
. Hallar la razón, y la suma y el producto de los  primeros términos
primeros términos
Los datos que tenemos son
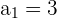

Usando la fórmula
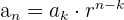
Podemos obtener el valor de

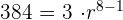
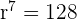
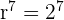
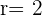
Con la fórmula
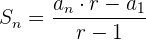
Podemos obtener la suma de los primeros 8 términos

Ahora consideramos la fórmula de producto
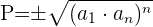
Para obtener el producto de los primeros
 términos
términos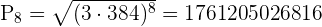
Medios aritméticos y geométricos
Escribir tres medios artméticos entre  y
y 
Tenemos los datos


Usando la fórmula
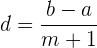
Podemos obtener el valor de

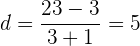
Finalmente

Escribir tres medios artméticos entre  y
y 
Tenemos los datos


Usando la fórmula
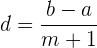
Podemos obtener el valor de

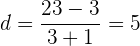
Finalmente

Escribir tres medios artméticos entre  y
y 
Tenemos los datos


Usando la fórmula
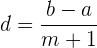
Podemos obtener el valor de

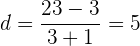
Finalmente

Interpolar tres medios geométricos entre  y
y 
Tenemos los datos

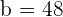
Usando la fórmula
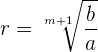
Podemos obtener el valor de


Finalmente
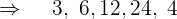
Interpolar tres medios geométricos entre  y
y 
Tenemos los datos

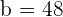
Usando la fórmula
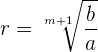
Podemos obtener el valor de


Finalmente
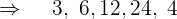
Encuentra la fracción generatriz
Encontrar la fracción generatriz de 
Reescribimos el número de la siguiente manera
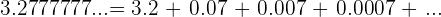
Tenemos una progresión geométrica decreciente ilimitada
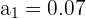
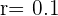
Entonces
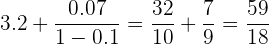
Encontrar la fracción generatriz de 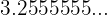
Reescribimos el número de la siguiente manera
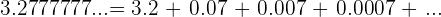
Tenemos una progresión geométrica decreciente ilimitada
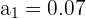
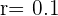
Entonces
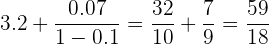
Encontrar la fracción generatriz de 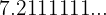
Reescribimos el número de la siguiente manera
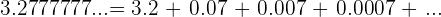
Tenemos una progresión geométrica decreciente ilimitada
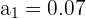
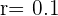
Entonces
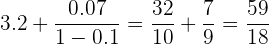
Encontrar la fracción generatriz de 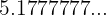
Reescribimos el número de la siguiente manera
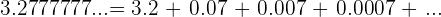
Tenemos una progresión geométrica decreciente ilimitada
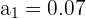
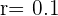
Entonces
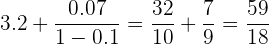
Encontrar la fracción generatriz de 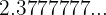
Reescribimos el número de la siguiente manera
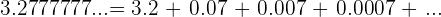
Tenemos una progresión geométrica decreciente ilimitada
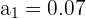
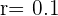
Entonces
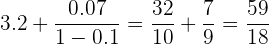
Geométricos
Hallar los ángulos de un cuadrilátero convexo, sabiendo que están en progresión aritmética, siendo 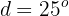
La suma de los ángulos interiores de un cuadrilátero es 360º
360 = [(a1 + a4) · 4]/2
a4 = a1 + 3 · 25
360= [( a1 + a1 + 3 · 25) · 4]/2
a1 = 105/2 = 52º 30'
a2 = 77º 30'
a3 = 102º 30'
a4 = 127º 30'
Hallar los ángulos de un cuadrilátero convexo, sabiendo que están en progresión aritmética, siendo 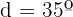
La suma de los ángulos interiores de un cuadrilátero es 360º
360 = [(a1 + a4) · 4]/2
a4 = a1 + 3 · 25
360= [( a1 + a1 + 3 · 25) · 4]/2
a1 = 105/2 = 52º 30'
a2 = 77º 30'
a3 = 102º 30'
a4 = 127º 30'
Hallar los ángulos de un hexágono convexo, sabiendo que están en progresión aritmética, siendo 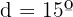
La suma de los ángulos interiores de un cuadrilátero es 360º
360 = [(a1 + a4) · 4]/2
a4 = a1 + 3 · 25
360= [( a1 + a1 + 3 · 25) · 4]/2
a1 = 105/2 = 52º 30'
a2 = 77º 30'
a3 = 102º 30'
a4 = 127º 30'
El cateto menor de un triángulo rectángulo mide 8 cm. Calcula los otros dos, sabiendo que los lados del triángulo forman una progresión aritmética
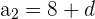
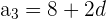
El teorema de Pitágoras nos dice que en un triángulo rectángulo la hipotenusa al cuadrado es igual a la suma de los catetos al cuadrado
(8 + 2d)² = (8 + d)² + 8^2

La solución negativa no es válida porque no existen lados negativos

El cateto menor de un triángulo rectángulo mide 5 cm. Calcula los otros dos, sabiendo que los lados del triángulo forman una progresión aritmética
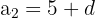
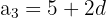
El teorema de Pitágoras nos dice que en un triángulo rectángulo la hipotenusa al cuadrado es igual a la suma de los catetos al cuadrado
(5 + 2d)² = (5 + d)² + 5^2

La solución negativa no es válida porque no existen lados negativos
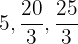
Resumir con IA:
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
el ejercicio 2 de sucesiones esta mal correjido ya que te dan el quinto y sexto termino, la diferencia es 12, y se ha copiado y pegado la respuesta del 1 en el 2
Hola podrías hacerme el favor de darme mas detalles pues no encontré el ejercicio que mencionas, nos ayudaría mucho.
en el ejercicio Nro. 5 hay una inconsistencia: para hallar a 1 seria 479 = a1 + 39(5) entonces 39*5 = 195 —- al despejar 479 -195 = a1 el resultado seria a1 = 284 ___ que seria el primer termino de la progresion …. entonces la progresion quedaria, así:
284 , 289 , 294 , 299 , 304 , 309 ,314 ,319, 324, 329, 334…
Hola agradecemos tus observaciones, pero no encontré el ejercicio que mencionas para poder corregirlo, podrías ser mas especifico seria de mucha ayuda.
hola podrias darme una idea de como podria hacer este ejercicio aplicando al formula CORRECTA Pedro ha decidido tomar un tour en sus vacaciones, para lo cual decide ahorrar de tal forma que el primer mes ahorra $ 300 y, luego, cada mes ahorra 3 veces lo ahorrado el mes anterior y así sucesivamente. ¿Cuánto ahorra al noveno mes?
Una disculpa, pero hubo una confusión con los artículos y se corrigió otro, te agradecemos tu paciencia y ahora si se corrigió, si no fuera así puedes mencionarlo otra vez y trabajaremos en ello.
50,45,39,32,