Capítulos
Sean bienvenidos a nuestra sección de Ejercicios de Progresiones Geométricas. Las progresiones geométricas son una fascinante área de las matemáticas que se encuentra en numerosos contextos, desde
crecimiento exponencial hasta cálculos financieros. A lo largo de esta sección, les proporcionaremos soluciones detalladas a una variedad de problemas que involucran progresiones geométricas, con el objetivo de fortalecer su comprensión y habilidades en este tema.
Cada ejercicio resuelto se presenta de manera clara y sistemática, guiándolos paso a paso a través del proceso de resolución. Exploraremos conceptos como el término general, la suma de términos y otras propiedades clave de las progresiones geométricas. Estos ejercicios no solo les permitirán comprender mejor la teoría, sino que también les brindarán herramientas prácticas para enfrentar problemas del mundo real que involucren este tipo de progresiones.
Les animamos a sumergirse en estos ejercicios resueltos, aprovechando esta oportunidad para consolidar sus conocimientos y aplicar las progresiones geométricas de manera efectiva en diversos escenarios matemáticos y prácticos.
Ejercicios
1El 2º término de una progresión geométrica es 
, y el 5º es 
. Escribir la progresión.
El 2º término de una progresión geométrica es , y el 5º es .
Escribir la progresión.
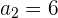
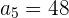
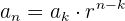
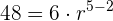
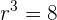
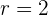
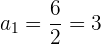
2El 1er término de una progresión geométrica es 
, y el 8º es 
. Hallar la razón, y la suma y el producto de los 8 primeros términos.
El 1er término de una progresión geométrica es , y el 8º es .
Hallar la razón, y la suma y el producto de los 8 primeros términos.
;
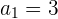
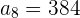Calculando la razón
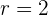
Suma de n- términos:
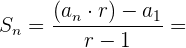
Producto de n-términos:
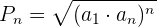
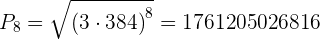
3Interpolar tres medios geométricos entre y .
Interpolar tres medios geométricos entre y .
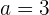
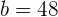
Calculando la razón:
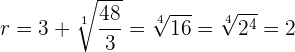
Escribir los términos:
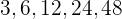
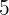términos de la progresión : Calcular la suma de los primeros 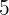términos de la progresión :
5Calcular la suma de los 5 términos de la progresión geométrica decreciente ilimitada: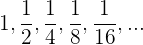 
Calcular la suma de los términos de la progresión geométrica
decreciente ilimitada:
Calculamos la razón :
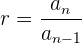
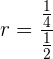
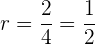
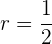
Usamos la formula para la suma de n términos.
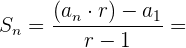
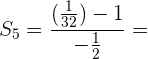
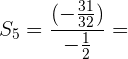
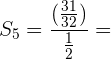
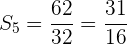
6Calcular el producto de los primeros 5 términos de la progresión:
Calcular el producto de los primeros 5 términos de la progresión:
Usamos la formula para el producto de n términos:
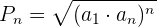
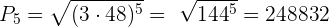
Juan ha comprado 20 libros. Por el 1º ha pagado 1€ por el 2º 2 €, por el 3º 4 €, por el 4º 8 € y así sucesivamente. ¿Cuánto ha pagado por los libros?
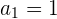
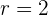
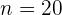
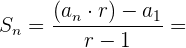
Calculamos el termino numero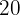 
:
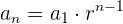
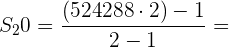
, se obtiene otro, en el que volvemos a hacer la misma operación, y así se continua indefinidamente. Calcular la suma de las áreas de los infinitos cuadrados. Uniendo los puntos medios de los lados de un cuadrado de lado , se obtiene otro, en el que volvemos a hacer la misma operación, y así se continua indefinidamente.
Calcular la suma de las áreas de los infinitos cuadrados.
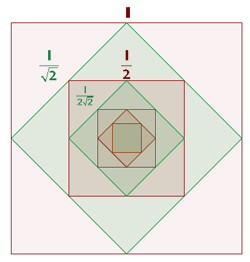
Por el teorema de Pitagoras es que podemos calcular el segundo termino de la sucesión, el cual es:
Teniendo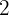 
términos, podemos calcular la razón:
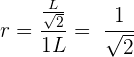
La sucesión es :
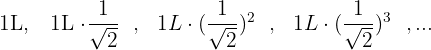
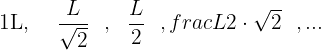
Elevamos cada termino al cuadrado para poder visualizar la progresión de una forma mas simple:
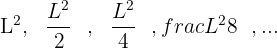
Aplicamos la formula para la suma de n términos, usando el concepto de limite, recordamos que cuando n tiende a infinito en el denominador, el valor de la fracción tiende a cero.
9Hallar la fracción generatriz de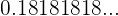 
Hallar la fracción generatriz de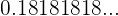
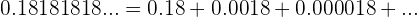
Es una progresión geométrica decreciente ilimitada.
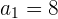
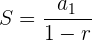
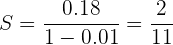
10Encontrar la fracción generatriz de 
Encontrar la fracción generatriz de
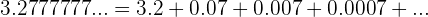
Tenemos una progresión geométrica decreciente ilimitada
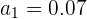
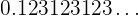
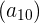se calcula usando la fórmula de la progresión geométrica: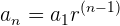 
donde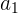 
es la inversión inicial, 
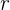es la razón de crecimiento (1 + tasa de interés), y 
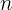es el número de meses. Entonces,
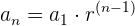
donde 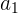es el monto del préstamo, 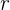es la razón de crecimiento (1 + tasa de interés), y 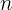es el número de meses. Entonces, terminamos pagando un total de
Es decir, hemos pagado un total de 17,103€ - 10,000€ = 7,103€ como interés.
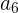se calcula utilizando la fórmula de progresión geométrica: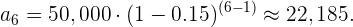 
. Entonces, buscamos un 
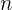tal que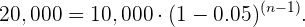 
Resolvemos para :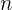
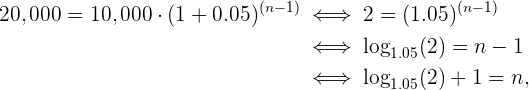
donde 
, es decir, requerimos 16 años para duplicar nuestra inversión.
El 2º término de una progresión geométrica es , y el 5º es . Escribir la progresión.
El 2º término de una progresión geométrica es , y el 5º es .
Escribir la progresión.
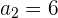
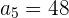
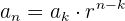
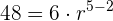
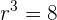
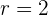
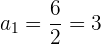
El 1er término de una progresión geométrica es , y el 8º es . Hallar la razón, y la suma y el producto de los 8 primeros términos.
El 1er término de una progresión geométrica es , y el 8º es .
Hallar la razón, y la suma y el producto de los 8 primeros términos.
;
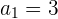
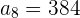Calculando la razón
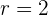
Suma de n- términos:
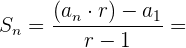
Producto de n-términos:
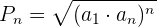
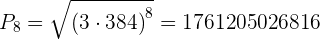
Interpolar tres medios geométricos entre y .
Interpolar tres medios geométricos entre y .
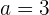
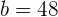
Calculando la razón:
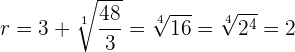
Escribir los términos:
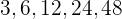
Calcular la suma de los primeros 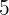términos de la progresión :
Calcular la suma de los primeros 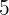términos de la progresión :
Calcular la suma de los 5 términos de la progresión geométrica decreciente ilimitada: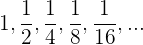
Calcular la suma de los términos de la progresión geométrica
decreciente ilimitada:
Calculamos la razón :
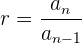
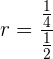
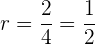
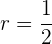
Usamos la formula para la suma de n términos.
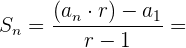
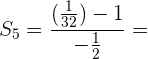
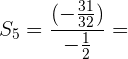
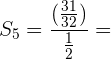
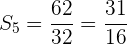
Calcular el producto de los primeros 5 términos de la progresión:
Calcular el producto de los primeros 5 términos de la progresión:
Usamos la formula para el producto de n términos:
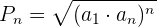
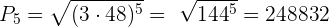
Juan ha comprado 20 libros. Por el 1º ha pagado 1€ por el 2º 2 €, por el 3º 4 €, por el 4º 8 € y así sucesivamente. ¿Cuánto ha pagado por los libros?
Juan ha comprado 20 libros. Por el 1º ha pagado 1€ por el 2º 2 €, por el 3º 4 €, por el 4º 8 € y así sucesivamente. ¿Cuánto ha pagado por los libros?
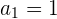
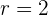
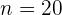
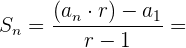
Calculamos el termino numero :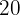
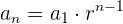
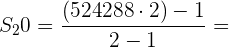
Uniendo los puntos medios de los lados de un cuadrado de lado , se obtiene otro, en el que volvemos a hacer la misma operación, y así se continua indefinidamente. Calcular la suma de las áreas de los infinitos cuadrados.
Uniendo los puntos medios de los lados de un cuadrado de lado , se obtiene otro, en el que volvemos a hacer la misma operación, y así se continua indefinidamente.
Calcular la suma de las áreas de los infinitos cuadrados.
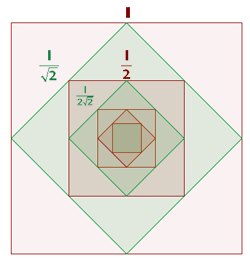
Por el teorema de Pitagoras es que podemos calcular el segundo termino de la sucesión, el cual es:
Teniendo 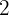términos, podemos calcular la razón:
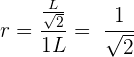
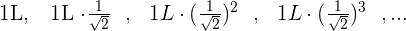
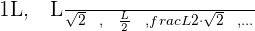
Elevamos cada termino al cuadrado para poder visualizar la progresión de una forma mas simple:
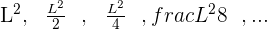
Aplicamos la formula para la suma de n términos, usando el concepto de limite, recordamos que cuando n tiende a infinito en el denominador, el valor de la fracción tiende a cero.
Hallar la fracción generatriz de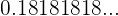
Hallar la fracción generatriz de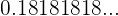
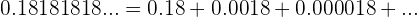
Es una progresión geométrica decreciente ilimitada.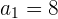
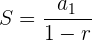
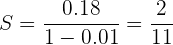
Encontrar la fracción generatriz de
Encontrar la fracción generatriz de
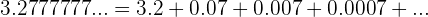
Tenemos una progresión geométrica decreciente ilimitada
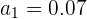
Encuentra la fracción generatriz del número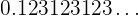
El número se puede representar de la forma
Supongamos que se realiza una inversión inicial de 5,000€ con una tasa de interés fija del 8% mensual. ¿Cuánto valdrá la inversión después de 10 meses si los rendimientos son reinvertidos en una progresión geométrica?
Para una inversión inicial de 5,000€ con una tasa de interés fija del 8% mensual, después de 10 meses, el valor de la inversión 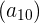se calcula usando la fórmula de la progresión geométrica:
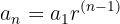
donde 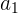es la inversión inicial, 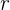es la razón de crecimiento (1 + tasa de interés), y 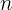es el número de meses. Entonces,
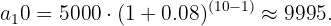
Un préstamo de 10,000€ a devolver en 12 meses con una tasa de interés del 5% mensual se amortiza mensualmente mediante una progresión geométrica. ¿Cuánto se habrá pagado al final de los 12 meses solamente en intereses?
La cuota mensual de amortización para un préstamo de 10,000 euros a devolver en 12 meses con una tasa de interés del 5% mensual se puede calcular utilizando la fórmula de la progresión geométrica:
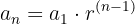
donde 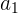es el monto del préstamo, 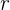es la razón de crecimiento (1 + tasa de interés), y 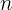es el número de meses. Entonces, terminamos pagando un total de
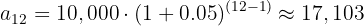
Es decir, hemos pagado un total de 17,103€ - 10,000€ = 7,103€ como interés.
El valor de un activo disminuye en un 15% mensual. Si el valor inicial es de 50,000 euros, ¿cuánto valdrá el activo después de 6 meses en una progresión geométrica de depreciación?
Si el valor de un activo disminuye en un 15% mensual, después de 6 meses, el valor del activo 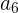se calcula utilizando la fórmula de progresión geométrica:
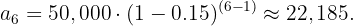
Supongamos que se realiza una inversión inicial de 10,000€ con una tasa de interés fija del 5% anual. ¿Cuántos años debemos esperar para duplicar nuestra inversión?
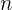Queremos encontrar la cantidad de años que le toma a la inversión llegar a 20,000€. Recordemos que la progresión geométrica es dada por . Entonces, buscamos un tal que
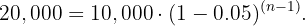
Resolvemos para :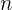
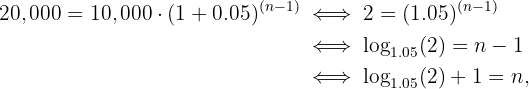
donde , es decir, requerimos 16 años para duplicar nuestra inversión.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en el ejercicio Nro. 5 hay una inconsistencia: para hallar a 1 seria 479 = a1 + 39(5) entonces 39*5 = 195 —- al despejar 479 -195 = a1 el resultado seria a1 = 284 ___ que seria el primer termino de la progresion …. entonces la progresion quedaria, así:
284 , 289 , 294 , 299 , 304 , 309 ,314 ,319, 324, 329, 334…
Hola agradecemos tus observaciones, pero no encontré el ejercicio que mencionas para poder corregirlo, podrías ser mas especifico seria de mucha ayuda.
Calcula los tres términos que siguen en estas sucesiones a partir de los datos que se dan.
a) a_1 = 3 a n + 1 =3+a n
b) a_1 = – 1 a n + 1 =n-2a n
hola podrias darme una idea de como podria hacer este ejercicio aplicando al formula CORRECTA Pedro ha decidido tomar un tour en sus vacaciones, para lo cual decide ahorrar de tal forma que el primer mes ahorra $ 300 y, luego, cada mes ahorra 3 veces lo ahorrado el mes anterior y así sucesivamente. ¿Cuánto ahorra al noveno mes?
Una disculpa, pero hubo una confusión con los artículos y se corrigió otro, te agradecemos tu paciencia y ahora si se corrigió, si no fuera así puedes mencionarlo otra vez y trabajaremos en ello.
50,45,39,32,
No se corrigió nada