Ejercicios propuestos
Hallar el término general de las siguientes sucesiones:
1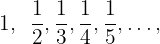 : El numerador es constante y el denominador es una progresión aritmética de
: El numerador es constante y el denominador es una progresión aritmética de 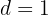 por lo tanto el n-esimo termino seria
por lo tanto el n-esimo termino seria 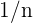 :
: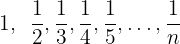
2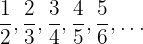 : El numerador es una progresión aritmética con una
: El numerador es una progresión aritmética con una 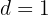 y el denominador también es una progresión aritmética con una
y el denominador también es una progresión aritmética con una 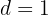 .
.
Y por tanto el n-esimo termino seria 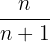
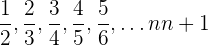
3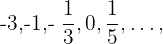 : En esta sucesión se han simplificado algunas fracciones,
: En esta sucesión se han simplificado algunas fracciones,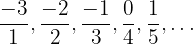
Con la progresión de esta manera observamos que el numerador es una progresión aritmética con una  que comienza en
que comienza en  y el denominador es una progresión aritmética de
y el denominador es una progresión aritmética de 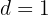 , entonces
, entonces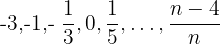
4 : Si prescindimos del signo es una progresión aritmética con una
: Si prescindimos del signo es una progresión aritmética con una 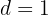 que inicia en
que inicia en  .
.
Por ser los términos impares los negativos multiplicamos por  y obtenemos
y obtenemos
5 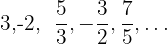 : Reescribimos la sucesión como
: Reescribimos la sucesión como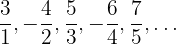
Si prescindimos del signo, el numerador es una progresión aritmética con una 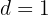 que inicia en
que inicia en  y el denominador es una progresión aritmética de
y el denominador es una progresión aritmética de 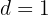 .
.
Por ser los términos pares los negativos multiplicamos por 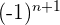 y obtenemos:
y obtenemos: 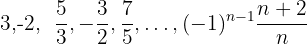
6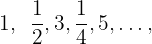 : Notemos que es una sucesión oscilante. Los términos impares forman progresión aritmética con
: Notemos que es una sucesión oscilante. Los términos impares forman progresión aritmética con 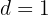 , si no tenemos en cuenta los términos pares.
, si no tenemos en cuenta los términos pares.
El denominador de los términos pares forman progresión aritmética con una 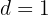 . Entonces
. Entonces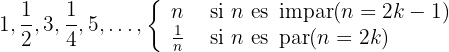
7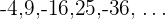 : Reescribimos como
: Reescribimos como 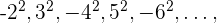 Si prescindimos del signo y del exponente tenemos una progresión aritmética con una
Si prescindimos del signo y del exponente tenemos una progresión aritmética con una 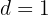 .
.
Por estar los términos al cuadrado, tenemos que elevar el término general al cuadrado.
Por ser los términos impares los negativos multiplicamos por  y obtenemos
y obtenemos
8 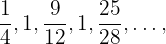 : Reescribimos como
: Reescribimos como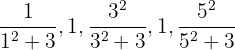 Notemos que es una sucesión oscilante.
Notemos que es una sucesión oscilante.
El numerador de los términos impares forman progresión aritmética con una 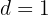 , si no tenemos en cuenta los términos pares. Por estar los términos al cuadrado, tenemos que elevar el término general al cuadrado.
, si no tenemos en cuenta los términos pares. Por estar los términos al cuadrado, tenemos que elevar el término general al cuadrado.
El primer sumando del denominador (prescindiendo del cuadrado) es una progresión aritmética de 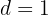 (sin contar los términos pares).
(sin contar los términos pares).
El término general lo tenemos que elevar al cuadrado y sumarle 3 .
Y los términos pares forman una sucesión constante, por tanto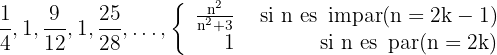
Estudia la monotonía, la convergencia o divergencia y las cotas (si existen) de las siguientes sucesiones:
1 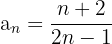 : Escribamos primero los primeros términos
: Escribamos primero los primeros términos 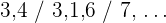 Notemos que la sucesión va decreciendo, entonces
Notemos que la sucesión va decreciendo, entonces 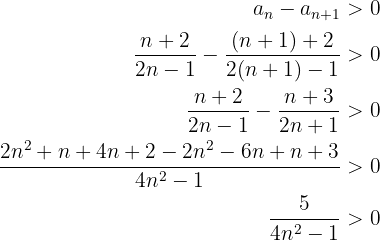
Puesto que la desigualdad se cumple para cualquier valor de  , la sucesión es monótona estrictamente decreciente.
, la sucesión es monótona estrictamente decreciente.
Ademas, notemos lo siguiente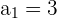
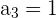
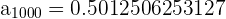
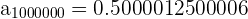 Notemos que el límite es
Notemos que el límite es  y por tanto es una sucesión convergente.
y por tanto es una sucesión convergente.
Por ser decreciente,  es una cota superior. Y
es una cota superior. Y  es una cota inferior, el ínfimo o extremo inferior. Por tanto la sucesión está acotada
es una cota inferior, el ínfimo o extremo inferior. Por tanto la sucesión está acotada 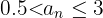
2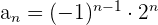 : Observando los primeros términos
: Observando los primeros términos 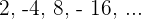 concluimos que: No es monótona, no es convergente ni divergente y no está acotada.
concluimos que: No es monótona, no es convergente ni divergente y no está acotada.
3 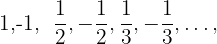 : Puesto que oscila entre positivos y negativos no es monótona, es convergente porque el límite
: Puesto que oscila entre positivos y negativos no es monótona, es convergente porque el límite  .Ademas ya que esta acotada superiormente por
.Ademas ya que esta acotada superiormente por  y acotada interiormente por
y acotada interiormente por  , esta acotada
, esta acotada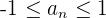
Escribe una sucesión:
- Monótona no acotada
- Acotada, no monótona
- No acotada, no monótona
- No acotada, convergente
- Acotada, divergente
- Acotada, no convergente
- No monótona, convergente
- No monótona, divergente
¿Buscas clases de algebra basica? ¡Están en Superprof!
1Monótona no acotada: 
2 Acotada, no monótona: 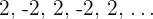
3No acotada, no monótona: 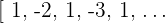
4No acotada, convergente: Es imposible
5 Acotada, divergente: Es imposible
6 Acotada, no convergente: 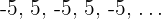
7 No monótona, convergente: 
8 No monótona, divergente: 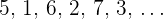
Hallar los ángulos de un cuadrilátero convexo, sabiendo que están en progresión aritmética, siendo 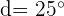
Sabemos que la suma de los ángulos interiores de un cuadrilátero es 360º por lo que sustituyendo en la fórmula de la suma de los primeros términos obtenemos:
También, sabemos que entre el primer y cuarto término existe la siguiente relación: 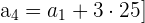
Sustituyendo la segunda expresión en la primera obtenemos:
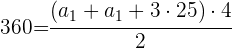
Entonces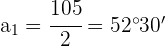
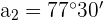
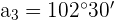

El cateto menor de un triángulo rectángulo mide  cm. Calcula los otros dos, sabiendo que los lados del triángulo forman una progresión aritmética.
cm. Calcula los otros dos, sabiendo que los lados del triángulo forman una progresión aritmética.
Tenemos que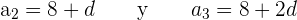
Aplicamos el teorema de Pitágoras: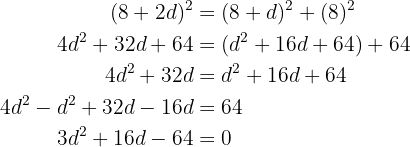
Resolvemos mediante la formula general para ecuaciones de segundo grado: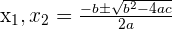
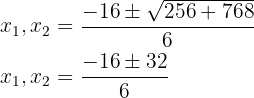
entonces
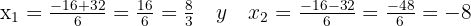
Cómo el resultado no puede ser negativo, obtenemos que  y entonces los lados del triangulo miden
y entonces los lados del triangulo miden  .
.
Uniendo los puntos medios de los lados de un cuadrado de lado  , se obtiene otro cuadrado, en el que volvemos a hacer la misma operación, y así se continua indefinidamente. Calcular la suma de las áreas de los infintos cuadrados.
, se obtiene otro cuadrado, en el que volvemos a hacer la misma operación, y así se continua indefinidamente. Calcular la suma de las áreas de los infintos cuadrados.
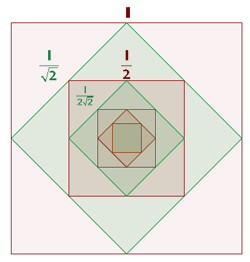
Por el teorema de Pitagoras es que podemos calcular el segundo termino de la sucesión, el cual es:  Teniendo
Teniendo 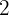 términos, podemos calcular la razón:
términos, podemos calcular la razón: 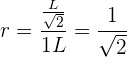
La sucesión es : 
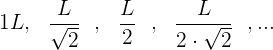
Elevamos cada termino al cuadrado para poder visualizar la progresión de una forma mas simple: 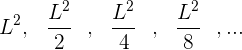
Aplicamos la formula para la suma de n términos, usando el concepto de limite, recordamos que cuando n tiende a infinito en el denominador, el valor de la fracción tiende a cero. 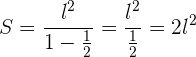
Demuestra que la sucesión 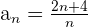 tiene límite 2. Averigua los términos cuya distancia a 2 es menor que 0.1.
tiene límite 2. Averigua los términos cuya distancia a 2 es menor que 0.1.
Para averiguar los términos de la sucesión 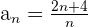 cuya distancia a
cuya distancia a  es menos a
es menos a 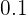 , tenemos que resolver la siguiente desigualdad:
, tenemos que resolver la siguiente desigualdad: 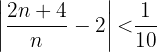 operando, obtenemos que
operando, obtenemos que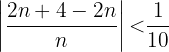 entonces
entonces 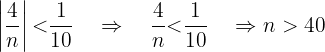
A partir de 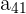 la distancia a
la distancia a  será menor que una decima.
será menor que una decima.
Probar que la sucesión  tiene por limite 4 y averiguar cuántos términos de la sucesión están fuera del entorno
tiene por limite 4 y averiguar cuántos términos de la sucesión están fuera del entorno 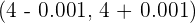 .
.
Para averiguar los términos de la sucesión  cuya distancia a
cuya distancia a  quedan fuera del entorno
quedan fuera del entorno 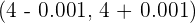 , resolvemos la siguiente desigualdad:
, resolvemos la siguiente desigualdad: 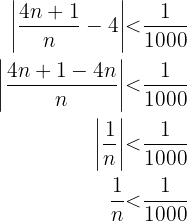 entonces
entonces 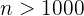 y por tanto quedan fuera del entorno los mil primeros términos de la sucesión.
y por tanto quedan fuera del entorno los mil primeros términos de la sucesión.
Demuestra que la sucesión 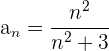 tiene por limite 1 y averiguar cuántos términos de la sucesión están fuera del entorno
tiene por limite 1 y averiguar cuántos términos de la sucesión están fuera del entorno  .
.
Para averiguar los términos de la sucesión que quedan fuera del entorno  , resolvemos la siguiente desigualdad
, resolvemos la siguiente desigualdad 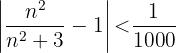 entonces
entonces 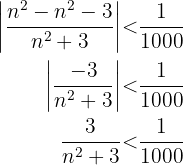 por tanto
por tanto 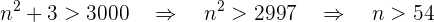
Los primeros  términos quedan fuera del entorno.
términos quedan fuera del entorno.
Demuestra que la sucesión 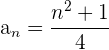 tiene por limite
tiene por limite 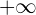 . Y calcula cuántos términos de la sucesión son menores que un millón.
. Y calcula cuántos términos de la sucesión son menores que un millón.
Para averiguar cuántos son los términos de la sucesión 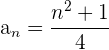 que tienen por límite
que tienen por límite 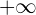 , tenemos que resolver lo siguiente:
, tenemos que resolver lo siguiente: 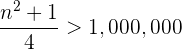 Operando
Operando 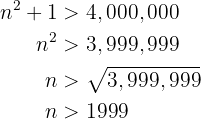
No llegan al millón los 1999 primeros términos de la sucesión.
¿Y si pruebas con un profe mates de Superprof? Nota: Infinito no es un número, las operaciones que realizamos con ∞ son simplemente un recurso para ayudarnos a resolver límites.
Calcula los siguientes límites:
1 Tenemos que  Factorizando
Factorizando 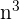 :
: 
2 En principio tenemos que 
Operando 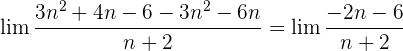
Dividimos cada factor tanto del numerador como del denominador por 
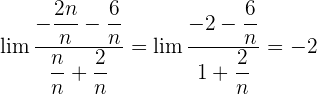
3 En principio obtenemos que  Pero si operamos
Pero si operamos 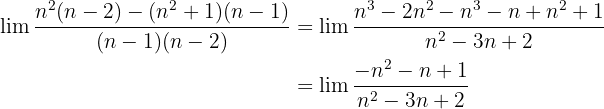
Dividimos cada factor tanto del numerador como del denominador por 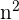 obteniendo
obteniendo

Calcula los siguientes límites:
1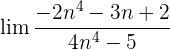 :
:
En principio 
Dividimos cada factor tanto del numerador como del denominador por 

2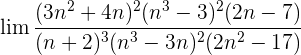 :
: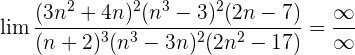
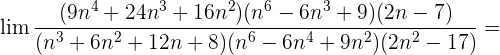
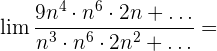
Dividimos cada factor tanto del numerador como del denominador por 

3 :
: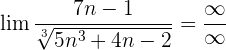
Dividimos cada factor tanto del numerador como del denominador por  , recuerda que cuando la
, recuerda que cuando la  dentro de la raíz cubica pasa como
dentro de la raíz cubica pasa como 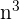
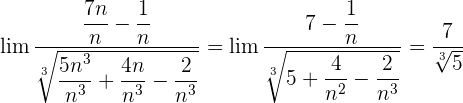
4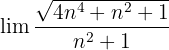 :
:
Dividimos cada factor tanto del numerador como del denominador por 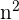 , recuerda que cuando la
, recuerda que cuando la 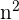 dentro de la raíz pasa como
dentro de la raíz pasa como 

5  :
: 
Separando 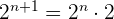 y lo mismo para
y lo mismo para 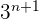 , posteriormente dividiendo por
, posteriormente dividiendo por 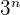
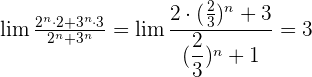
Calcula los siguientes límites:
1  :
:
Dividimos cada factor tanto del numerador como del denominador por 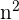

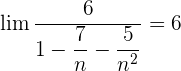
2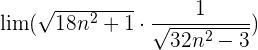 :
: 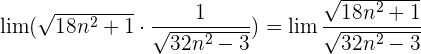
Dividimos cada factor tanto del numerador como del denominador dentro de la raíz por 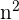
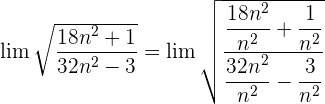

Calcula los siguientes límites:
1  :
:
Evaluando directamente tanto el límite de la potencia como el límite de la base: 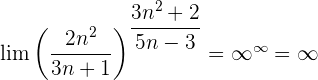
2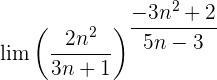 :
:
Evaluando directamente tanto el límite de la potencia como el límite de la base: 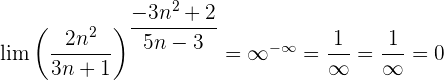
3 :
:
Evaluando directamente tanto el límite de la potencia como el límite de la base: 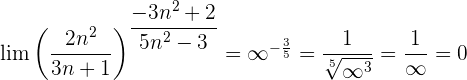
4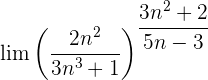 :
:
Evaluando directamente tanto el límite de la potencia como el límite de la base: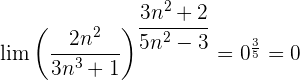
5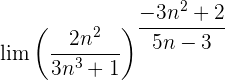 :
:
Evaluando directamente tanto el límite de la potencia como el límite de la base: 
Calcula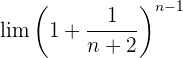
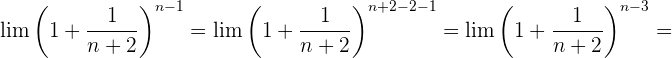

Calcula el siguiente límite: 
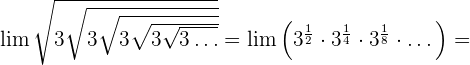
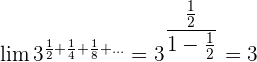
En este ejercicio aplicamos en el penúltimo paso, la formula de la progresión geométrica infinita.
Resumir con IA:
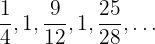
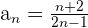
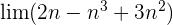

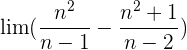


Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
el ejercicio 2 de sucesiones esta mal correjido ya que te dan el quinto y sexto termino, la diferencia es 12, y se ha copiado y pegado la respuesta del 1 en el 2
Hola podrías hacerme el favor de darme mas detalles pues no encontré el ejercicio que mencionas, nos ayudaría mucho.
en el ejercicio Nro. 5 hay una inconsistencia: para hallar a 1 seria 479 = a1 + 39(5) entonces 39*5 = 195 —- al despejar 479 -195 = a1 el resultado seria a1 = 284 ___ que seria el primer termino de la progresion …. entonces la progresion quedaria, así:
284 , 289 , 294 , 299 , 304 , 309 ,314 ,319, 324, 329, 334…
Hola agradecemos tus observaciones, pero no encontré el ejercicio que mencionas para poder corregirlo, podrías ser mas especifico seria de mucha ayuda.
hola podrias darme una idea de como podria hacer este ejercicio aplicando al formula CORRECTA Pedro ha decidido tomar un tour en sus vacaciones, para lo cual decide ahorrar de tal forma que el primer mes ahorra $ 300 y, luego, cada mes ahorra 3 veces lo ahorrado el mes anterior y así sucesivamente. ¿Cuánto ahorra al noveno mes?
Una disculpa, pero hubo una confusión con los artículos y se corrigió otro, te agradecemos tu paciencia y ahora si se corrigió, si no fuera así puedes mencionarlo otra vez y trabajaremos en ello.
50,45,39,32,