Capítulos
- Término general de una progresión geométrica.
- Interpolación de n términos en una progresión geométrica
- Suma de n términos consecutivos de una progresión geométrica
- Suma de los términos de una progresión geométrica decreciente
- Producto de dos términos equidistantes
- Producto de n términos consecutivos de una progresión geométrica
Las progresiones geométricas tienen distintas aplicaciones en la vida diaria como el cálculo de intereses de algún préstamo, cuando compras algún articulo o para medir crecimientos de población de alguna especie; te invito a conocer un poco de sus propiedades.
Una progresión geométrica es una sucesión en la que cada término se obtiene multiplicando al anterior por una cantidad fija r, llamada razón.
Ejemplo:
Si se tiene a un primer término a1=3 y a una razón r=4 se puede construir la siguiente progresión geométrica:
3, 12, 48, 192, ...
ya que al operar el primer término a1=3 con la razón r=4 se obtiene que:
3
3(4)=12
12(4)=48
48(4)=192, ...
Como observas, el 12 se obtiene multiplicando 3 por 4, que es la razón, y así sucesivamente hasta llegar al término deseado n.
Por otro lado, si se conocen dos términos consecutivos an y an+1 de la progresión geométrica y no se conoce la razón r, se puede calcular la razón r dividiendo dichos términos como lo indica la siguiente ecuación:
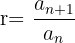
Ejemplo:
Se tiene la progresión geométrica: 3, 6, 12, 24, 48, ... observa que cualesquiera dos términos consecutivos tienen la razón r=2, ya que al aplicar la ecuación anterior se obtiene que:
r=6/3=2
r=12/6=2
r=24/12=2
r=48/24=2

Término general de una progresión geométrica.
El término general de una sucesión es la expresión an que permite conocer cualquier término en función de su posición n.
Al momento de querer conocer el valor del término general an, te puedes enfrentar a dos situaciones:
1Si conoces al primer término a1 y a la razón r . En este caso es posible conocer a cualquier otro término de la progresión con el uso de la siguiente fórmula:
an = a1 · rn-1
Ejemplo:
Tienes la siguiente progresión, y te piden calcular el valor del término de la posición 20:
3, 6, 12, 24, 48, ...
Identifica que a1=3, la razón r =2 y como te piden conocer el valor del término 20, entonces n=20; al sustituir estos valores en la fórmula obtienes que:
a20 = 3· 220-1 = 3· 219 = 1, 572, 864
Por lo tanto, el valor del término 20 es 1, 572, 864.
2Cuando no conoces el primer término a1 de la progresión geométrica, pero conoces cualquier otro término ak y a la razón r. En este caso es posible calcular cualquier termino an usando la siguiente ecuación:
an = ak · rn-k
Donde k es el número de la posición del término que conoces y n es la posición del término que deseas conocer.
Ejemplo:
Supón que ak es igual a 24, donde k=4 y la razón r=2, al sustituir los valores en la fórmula tienes que:
an = a4 · 2n-4
Ahora, si quieres conocer el valor de a1, se calcula de la siguiente manera:
a1 = 24· 21-4= (24)· 2-3 = (24)(1/8) =3
Ahora, en el caso de querer conocer el valor de a10 se calcula de la misma manera que el ejemplo anterior:
a10 = 24· 210-4= (24)· 26 = 1536
No olvides que n es la posición del término que deseas conocer.
Como te darás cuenta no importa qué termino an se quiere conocer, pues se calcula con la fórmula adecuada dependiendo la situación. Ya sea conociendo al primer término a1 o a cualquier otro ak de la progresión geométrica, junto con la razón r.
Interpolación de n términos en una progresión geométrica
Interpolar medios geométricos o proporcionales entre dos números a y b, es construir una progresión geométrica que tenga por extremos los elementos a y b, y a una cantidad determinada de valores intermedios. Para lograr esto, es necesario saber cuántos elementos m se quieren interpolar, y con esta información calcular la razón r adecuada. Ya que con r y el valor de a, se construye la progresión geométrica.
La fórmula para conocer a la razón r adecuada para interpolar a m medios geométricos entre a y b es la siguiente:
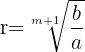
Ejemplo:
Interpolar 3 medios geométricos entre a=-2 y b=-4802. Primero se busca a la razón r adecuada.
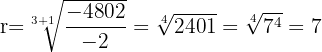
Ya que se sabe que r=7, se usa para construir la progresión geométrica tomando como primer valor al a=-2 y se va multiplicando por la razón r=7 sucesivamente, obteniendo:
-2, -14, -98, -686, -4802.
Observa que se han interpolado 3 números entre -2 y -4802, formando la progresión.
Ejemplo:
Interpolar tres medios geométricos entre a=3 y b=48. Primero se busca la razón r adecuada.
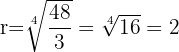
Observa que se usa la razón encontrada para construir la progresión geométrica, obteniendo:
3, 6, 12, 24 , 48.
De igual manera que el ejemplo anterior se han interpolado 3 números pero ahora entre 3 y 48, formando a la progresión deseada.
En conclusión, se pueden interpolar la cantidad de términos m que se necesiten, o deseen, entre a y b, sólo es cuestión de calcular la razón r adecuada haciendo uso de la fórmula.
Suma de n términos consecutivos de una progresión geométrica
Para lograr sumar a n términos consecutivos de una progresión geométrica, primero se necesita conocer la razón r, al primer término a1 , y al número de valores n que se desea sumar de la sucesión.
Ya que se conocen estos datos se hace uso de la fórmula:
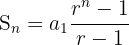
donde Sn es la suma de n términos consecutivos de una progresión geométrica.
Ejemplo:
Calcular la suma de los primeros 5 términos de la siguiente progresión: 3, 6, 12, 24, 48, ...
Se calcula a la razón r, dividiendo a dos valores consecutivos, como se vio en un principio
r=6/3 =2
ahora con r=2, n=5 y a1 =3 se sustituyen los valores en la fórmula, obteniendo que:
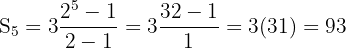
y con esto se conoce el resultado de sumar a los n términos solicitados, dando como resultado:
3 + 6 + 12 + 24 + 48 = 93
Observa que una ventaja de realizar la suma de n términos con este procedimiento es que se ahorra mucho trabajo, a diferencia de hacer la suma de manera directa, ya que existe la posibilidad de que la cantidad de términos n a sumar sea muy grande.
Suma de los términos de una progresión geométrica decreciente
Hay ocasiones donde se necesita sumar a todos los términos de una progresión geométrica decreciente ilimitada. Para que tenga sentido la suma es necesario que el valor de la razón esté comprendido entre -1 y 1, de lo contrario no es posible realizar la suma, ya que no tendría resultado numérico.
La fórmula que te ayuda a conocer el resultado de sumar a todos los términos
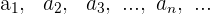
con -1 < r < 1 es:
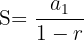
Con esta fórmula se calcula la suma de todos los términos de la progresión, es decir:

Ejemplo:
Calcular la suma de los términos de la progresión geométrica decreciente ilimitada, formada por a1=2 y r=0.5.
Recordemos que se debe tener al valor de r entre -1 y 1, y en nuestro caso r=0.5 , cumpliendo con la condición, significa que podemos seguir con el proceso.
Ahora se construye a la progresión:
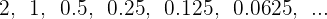
y así sucesivamente (los puntos suspensivos indican que el proceso sigue sin terminar).
Entonces ya con esto, se conoce el resultado de la suma de todos los términos, sustituyendo en la fórmula:
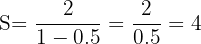
significa que
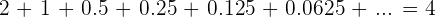
llegando así al resultado buscado.
¿Necesitas un profesor de matematicas?
La suma que trabajamos ahora es distinta a la anterior, ya que aquí se han sumado una cantidad ilimitada de términos (anteriormente la suma era de una cantidad finita de términos) por tal razón, fue necesario ocupar la fórmula mencionada.
Producto de dos términos equidistantes
Cuando se tiene una progresión geométrica, donde a1 es el primer término y an es el último, se entiende que dos valores son equidistantes, si se encuentran a la misma distancia tanto de un extremo como del otro de la progresión respectivamente, por ejemplo:
a2 equidista de an-1
a3 equidista de an-2
a4 equidista de an-3
y así sucesivamente.
Una propiedad indica que la multiplicación entre dos valores equidistantes, es igual al producto de los extremos de dicha progresión, es decir:
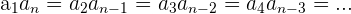
Ejemplo:
Si tenemos a la siguiente progresión geométrica:
5, 10, 20, 40, 80, 160
podemos ver que el producto de los extremos
5 (160) = 800
es igual al producto de cualquier pareja de términos equidistantes, por ejemplo:
10 (80) = 800
20 (40) = 800
esta propiedad tiene la ventaja de multiplicar solamente a los extremos, para que así se conozca el resultado de multiplicar a cualquier pareja de términos equidistantes, y además se puede necesitar para futuros resultados.
Producto de n términos consecutivos de una progresión geométrica
Si se busca multiplicar a una cantidad n de términos consecutivos de una progresión geométrica, es suficiente saber los valores de los extremos a1 y an , es decir, para conocer al producto de los términos
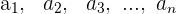
Se usa la fórmula:
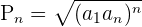
en otras palabras, la fórmula permite saber de manera efectiva, el resultado del producto siguiente:
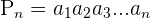
Ejemplo:
Calcular el producto de los 5 primeros términos de la progresión
3, 6, 12, 24, 48, ...
Aquí podemos ver que a1 =3 a5 =48 con n=5 entonces la sustitución queda:
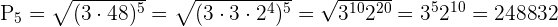
en otras palabras el resultado que se obtuvo es el siguiente:
(3) (6) (12) (24) (48) = 248, 832
y así como en la suma de n términos consecutivos, aquí también es más conveniente y práctico, conocer el resultado del producto con el uso de la fórmula pues se puede llegar a tener una gran cantidad de factores.
Te recordamos que en Superprof puedes encontrar a tu profe ideal, tanto si buscas un profesor de matematicas online o uno presencial.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
el ejercicio 2 de sucesiones esta mal correjido ya que te dan el quinto y sexto termino, la diferencia es 12, y se ha copiado y pegado la respuesta del 1 en el 2
Hola podrías hacerme el favor de darme mas detalles pues no encontré el ejercicio que mencionas, nos ayudaría mucho.
en el ejercicio Nro. 5 hay una inconsistencia: para hallar a 1 seria 479 = a1 + 39(5) entonces 39*5 = 195 —- al despejar 479 -195 = a1 el resultado seria a1 = 284 ___ que seria el primer termino de la progresion …. entonces la progresion quedaria, así:
284 , 289 , 294 , 299 , 304 , 309 ,314 ,319, 324, 329, 334…
Hola agradecemos tus observaciones, pero no encontré el ejercicio que mencionas para poder corregirlo, podrías ser mas especifico seria de mucha ayuda.
hola podrias darme una idea de como podria hacer este ejercicio aplicando al formula CORRECTA Pedro ha decidido tomar un tour en sus vacaciones, para lo cual decide ahorrar de tal forma que el primer mes ahorra $ 300 y, luego, cada mes ahorra 3 veces lo ahorrado el mes anterior y así sucesivamente. ¿Cuánto ahorra al noveno mes?
Una disculpa, pero hubo una confusión con los artículos y se corrigió otro, te agradecemos tu paciencia y ahora si se corrigió, si no fuera así puedes mencionarlo otra vez y trabajaremos en ello.
50,45,39,32,