
Los/las mejores profesores/as de Matemáticas que están disponibles
Sucesión entera
Se saca factor común de la potencia de mayor exponente.

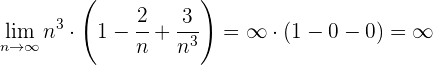
Regla práctica
El límite es  , dependiendo del signo del coeficiente de mayor grado.
, dependiendo del signo del coeficiente de mayor grado.


Sucesiones racionales
Ponemos a común denominador, y si obtenemos  resolvemos la indeterminación.
resolvemos la indeterminación.
Sucesiones irracionales
Multiplicamos y dividimos por el conjugado.
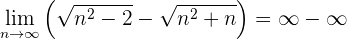

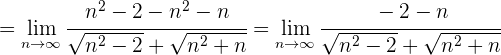

Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
el ejercicio 2 de sucesiones esta mal correjido ya que te dan el quinto y sexto termino, la diferencia es 12, y se ha copiado y pegado la respuesta del 1 en el 2
Hola podrías hacerme el favor de darme mas detalles pues no encontré el ejercicio que mencionas, nos ayudaría mucho.
en el ejercicio Nro. 5 hay una inconsistencia: para hallar a 1 seria 479 = a1 + 39(5) entonces 39*5 = 195 —- al despejar 479 -195 = a1 el resultado seria a1 = 284 ___ que seria el primer termino de la progresion …. entonces la progresion quedaria, así:
284 , 289 , 294 , 299 , 304 , 309 ,314 ,319, 324, 329, 334…
Hola agradecemos tus observaciones, pero no encontré el ejercicio que mencionas para poder corregirlo, podrías ser mas especifico seria de mucha ayuda.
hola podrias darme una idea de como podria hacer este ejercicio aplicando al formula CORRECTA Pedro ha decidido tomar un tour en sus vacaciones, para lo cual decide ahorrar de tal forma que el primer mes ahorra $ 300 y, luego, cada mes ahorra 3 veces lo ahorrado el mes anterior y así sucesivamente. ¿Cuánto ahorra al noveno mes?
Una disculpa, pero hubo una confusión con los artículos y se corrigió otro, te agradecemos tu paciencia y ahora si se corrigió, si no fuera así puedes mencionarlo otra vez y trabajaremos en ello.
50,45,39,32,