La estadística es una herramienta fundamental para el análisis y la interpretación de datos en diversas disciplinas, desde las ciencias sociales hasta las ingenierías. Comprender los conceptos estadísticos y saber aplicarlos correctamente es crucial para tomar decisiones informadas basadas en datos.
Esta sección de ejercicios resueltos está diseñada para ayudar a consolidar los conocimientos teóricos adquiridos en los temas de estadística. A través de la práctica con problemas reales, se busca desarrollar habilidades analíticas y fortalecer la capacidad para resolver situaciones estadísticas comunes y complejas.
Indica cuáles variables son cualitativas y cuáles cuantitativas
a Comida Favorita.
b Profesión que te gusta.
c Número de goles marcados por tu equipo favorito en la última temporada.
d Número de alumnos de tu Instituto.
e El color de los ojos de tus compañeros de clase.
f Coeficiente intelectual de tus compañeros de clase.
a Comida Favorita.
Cualitativa
b Profesión que te gusta.
Cualitativa
c Número de goles marcados por tu equipo favorito en la última temporada.
Cuantitativa
d Número de alumnos de tu Instituto.
Cuantitativa
e El color de los ojos de tus compañeros de clase.
Cualitativa
f Coeficiente intelectual de tus compañeros de clase.
Cuantitativa
De las siguientes variables indica cuáles son discretas y cuales continuas:
a Número de acciones vendidas cada día en la Bolsa.
b Temperaturas registradas cada hora en un observatorio.
c Período de duración de un automóvil.
d El diámetro de las ruedas de varios coches.
e Número de hijos de  familias.
familias.
f Censo anual de los españoles.
a Número de acciones vendidas cada día en la Bolsa.
Discreta
b Temperaturas registradas cada hora en un observatorio.
Continua
c Período de duración de un automóvil.
Continua
d El diámetro de las ruedas de varios coches.
Continua
e Número de hijos de  familias.
familias.
Discreta
f Censo anual de los españoles.
Discreta
Clasificar las siguientes variables en cualitativas o cuantitativas, y en discretas o continuas:
a La nacionalidad de una persona.
b Número de litros de agua contenidos en un depósito.
c Número de libros en un estante de librería.
d Suma de puntos tenidos en el lanzamiento de un par de dados.
e La profesión de una persona.
f El área de las distintas baldosas de un edificio.
a La nacionalidad de una persona.
Cualitativa
b Número de litros de agua contenidos en un depósito.
Cuantitativa y continua
c Número de libro en un estante de librería.
Cuantitativa y discreta
d Suma de puntos tenidos en el lanzamiento de un par de dados.
Cuantitativa y discreta
e La profesión de una persona.
Cualitativa
f El área de las distintas baldosas de un edificio.
Cuantitativa y continua
Las puntuaciones obtenidas por un grupo en una prueba han sido:

Construir la tabla de distribución de frecuencias y dibujar el polígono de frecuencias.
 | Recuento |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  | 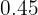 |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 | 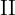 |  |  |  |  |
 |  |  |  |  |  |
 |
En la cuarta columna disponemos la frecuencia acumulada  .
.
En la primera casilla colocamos la primera frecuencia absoluta.
En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que ser igual a  .
.
En la quinta columna disponemos las frecuencias relativas,  , que
, que
son el resultado de dividir cada frecuencia absoluta por  .
.
En la sexta columna disponemos la frecuencia relativa acumulada  .
.
En la primera casilla colocamos la primera frecuencia relativa.
En la segunda casilla sumamos el valor de la frecuencia relativa acumulada anterior más la frecuencia relativa acumulada correspondiente y así sucesivamente hasta la última, que tiene que ser igual a  .
.
Polígono de frecuencias
En eje de abscisas van los datos y en el de ordenadas las frecuencias absolutas

El número de estrellas de los hoteles de una ciudad viene dado por la siguiente serie:

Construir la tabla de distribución de frecuencias y dibuja el diagrama de barras.
Pasos para construir la tabla de distribución de frecuencias y dibujar el diagrama de barras.
 | Recuento |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |
En la cuarta columna disponemos la frecuencia acumulada  .
.
En la primera casilla colocamos la primera frecuencia absoluta.
En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a  .
.
En la quinta columna disponemos las frecuencias relativas ( ) que
) que
son el resultado de dividir cada frecuencia absoluta por  .
.
En la sexta columna disponemos la frecuencia relativa acumulada  .
.
En la primera casilla colocamos la primera frecuencia relativa.
En la segunda casilla sumamos el valor de la frecuencia relativa acumulada anterior más la frecuencia relativa acumulada correspondiente y así sucesivamente hasta la última, que tiene que ser igual a  .
.
Diagrama de barras
En eje de abscisas van los datos y en el de ordenadas las frecuencias absolutas.

Las calificaciones de  alumnos han sido las siguientes:
alumnos han sido las siguientes:

Construir la tabla de distribución de frecuencias y dibuja el diagrama de barras.
Pasos para construir la tabla de distribución de frecuencias y dibujar el
diagrama de barras.
 |  |  |  |  |
 |  |  |  |  |
 1 1 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |
En la cuarta columna disponemos la frecuencia acumulada  .
.
En la primera casilla colocamos la primera frecuencia absoluta.
En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a  .
.
En la quinta columna disponemos las frecuencias relativas ( ) que son el resultado de dividir cada frecuencia absoluta por
) que son el resultado de dividir cada frecuencia absoluta por  .
.
En la sexta columna disponemos la frecuencia relativa acumulada  .
.
En la primera casilla colocamos la primera frecuencia relativa.
En la segunda casilla sumamos el valor de la frecuencia relativa acumulada anterior más la frecuencia relativa acumulada correspondiente y así sucesivamente hasta la última, que tiene que ser igual a 
Diagrama de barras
En eje de abscisas van los datos y en el de ordenadas las frecuencias absolutas.

Los pesos de los  empleados de una fábrica vienen dados por la siguiente tabla:
empleados de una fábrica vienen dados por la siguiente tabla:
| Peso |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
a Construir la tabla de frecuencias.
b Representar el histograma y el polígono de frecuencias.
aConstruir la tabla de frecuencias.
 |  |  |  |  | |
 |  |  |  |  |  |
 |  |  |  |  | 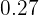 |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |
En la cuarta columna disponemos la frecuencia acumulada  .
.
En la primera casilla colocamos la primera frecuencia absoluta.
En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a  .
.
En la quinta columna disponemos las frecuencias relativas ( ) que son el resultado de dividir cada frecuencia absoluta por
) que son el resultado de dividir cada frecuencia absoluta por  .
.
En la sexta columna disponemos la frecuencia relativa acumulada  .
.
En la primera casilla colocamos la primera frecuencia relativa.
En la segunda casilla sumamos el valor de la frecuencia relativa acumulada anterior más la frecuencia relativa acumulada correspondiente y así sucesivamente hasta la última, que tiene que ser igual a  .
.
bRepresentar el histograma y el polígono de frecuencias.
Histograma
El polígono de frecuencias lo construimos uniendo los puntos medios de cada rectángulo

Los  alumnos de una clase han obtenido las siguientes puntuaciones sobre
alumnos de una clase han obtenido las siguientes puntuaciones sobre  , en un examen de Física:
, en un examen de Física:

aConstruir la tabla de frecuencias.
b Dibujar el histograma y el polígono de frecuencias.
a Construir la tabla de frecuencias.
 |  |  |  |  | |
 |  |  |  |  |  |
 |  |  |  |  | 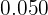 |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  | 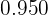 |
 |  |  |  | 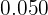 |  |
 |  |
En la cuarta columna disponemos la frecuencia acumulada  .
.
En la primera casilla colocamos la primera frecuencia absoluta.
En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a  .
.
En la quinta columna disponemos las frecuencias relativas ( ) que son el resultado de dividir cada frecuencia absoluta por
) que son el resultado de dividir cada frecuencia absoluta por  .
.
En la sexta columna disponemos la frecuencia relativa acumulada  .
.
En la primera casilla colocamos la primera frecuencia relativa.
En la segunda casilla sumamos el valor de la frecuencia relativa acumulada anterior más la frecuencia relativa acumulada correspondiente y así sucesivamente hasta la última, que tiene que ser igual a  .
.
b Dibujar el histograma y el polígono de frecuencias.
Histograma
El polígono de frecuencias lo construimos uniendo los puntos medios de cada rectángulo

Sea una distribución estadística que viene dada por la siguiente tabla:
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Calcular:
a La moda, mediana y media.
b El rango, desviación media, varianza y desviación típica.
Completamos la tabla con:
La frecuencia acumulada ( ) para calcular la mediana
) para calcular la mediana
El producto de la variable por su frecuencia absoluta ( ) para calcular la media
) para calcular la media
La desviación respecto a la media  y su producto por la frecuencia absoluta
y su producto por la frecuencia absoluta  para calcular la desviación media
para calcular la desviación media
El producto de la variable al cuadrado por su frecuencia absoluta (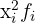 ) para calcular la varianza y la desviación típica
) para calcular la varianza y la desviación típica
 |  |  |  |  |  | 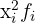 |
 |  |  |  |  |  |  |
 |  |  |  |  |  | 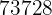 |
 |  |  |  | 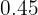 |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |
Moda
La moda es el valor que tiene mayor frecuencia absoluta.
Miramos en la columna de las  y la frecuencia absoluta mayor,
y la frecuencia absoluta mayor,  ,corresponde a
,corresponde a  .
.
 .
.
Mediana
Para calcular la mediana dividimos  entre
entre  y vemos que la casilla de las
y vemos que la casilla de las  donde se encuentra que la
donde se encuentra que la  mas cercana a
mas cercana a  es
es  y corresponde a
y corresponde a  .
.


Media
Calculamos la sumatoria de la variable por su frecuencia absoluta ( ) que es
) que es  y la dividimos por
y la dividimos por  .
.

Desviación media
Calculamos la sumatoria de de los productos de desviaciones respecto a la media por sus frecuencias absolutas correspondientes  que es
que es  y dividimos por
y dividimos por  .
.

Rango
Realizamos la la diferencia entre el mayor y el menor de los valores
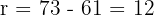 .
.
Varianza
Calculamos la sumatoria de  , la dividimos por
, la dividimos por  y al resultado le restaremos la media aritmética al cuadrado
y al resultado le restaremos la media aritmética al cuadrado 
 .
.
Desviación típica
Hacemos la raíz cuadrada de la varianza

Calcular la media, la mediana y la moda de la siguiente serie de números:

Creamos una tabla con las siguientes columnas:
Los valores de la variable ( ).
).
Las frecuencias absolutas ( ).
).
Las frecuencias acumuladas ( ) para calcular la mediana.
) para calcular la mediana.
El producto de la variable por su frecuencia absoluta ( ) para calcular la media.
) para calcular la media.
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |
Moda
La moda es el valor que tiene mayor frecuencia absoluta.
Miramos en la columna de las  y la frecuencia absoluta mayor,
y la frecuencia absoluta mayor,  , corresponde a
, corresponde a  .
.
 .
.
Mediana
Para calcular la mediana dividimos  entre
entre  y vemos que la casilla de las
y vemos que la casilla de las  donde se encuentra
donde se encuentra  corresponde a
corresponde a  .
.
 .
.
Media
Calculamos la sumatoria de la variable por su frecuencia absoluta ( ) que es
) que es  y la dividimos por
y la dividimos por  .
.
 .
.
Hallar la varianza y la desviación típica de la siguiente serie de datos:

Calculamos la media aritmética:
 .
.
Aplicamos la fórmula de la varianza:
 .
.
Realizamos la raíz cuadrada de la varianza:
 .
.
Hallar la media, mediana y moda de la siguiente serie de números:

Moda
La moda es  porque es el valor que más se repite.
porque es el valor que más se repite.
 .
.
Mediana
La serie tiene un número par de puntuaciones, la mediana será la media entre las dos puntuaciones centrales.
 .
.
Media
Aplicamos la fórmula de la media.
 .
.
Hallar la desviación media, la varianza y la desviación típica de la series de números siguientes:
1 
2 
1 
Media

Desviación media

Varianza
 .
.
Desviación típica
 .
.
2 
Media
 .
.
Desviación media
 .
.
Varianza

Desviación típica
 .
.
Se ha aplicado un test a los empleados de una fábrica, obteniéndose la siguiente tabla:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
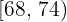 |  |
 |  |
Dibujar el histograma y el polígono de frecuencias acumuladas.
Agregamos una nueva columna donde disponemos las frecuencias acumuladas ( ):
):
En la primera casilla colocamos la primera frecuencia absoluta.
En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que ser igual a  .
.
 |  | |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
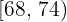 |  |  |
 |  |  |
 |

Dadas las series estadísticas:
a 
b 
Calcular:
La moda, la mediana y la media.
La desviación media, la varianza y la desviación típica
Los cuartiles  y
y  .
.
Los deciles  y
y  .
.
Los percentiles  y
y  .
.
a 
Moda
No existe moda porque todas las puntuaciones tienen la misma frecuencia.
Mediana
Ordenando los datos tenemos:

Por lo tanto la mediana es
 .
.
Media

Varianza

Desviación típica

Desviación media

Rango

Cuartiles

Deciles
Tenemos que la fórmula para la posición de los deciles está dada por

Por lo tanto, los deciles que buscamos están en las posiciones:

Percentiles
Tenemos que la fórmula para la posición de los percentiles está dada por

Por lo tanto, los percentiles que buscamos están en las posiciones:

b 
Moda
No existe moda porque todas las puntuaciones tienen la misma frecuencia.
Mediana
Ordenando los datos tenemos:

Por lo tanto la mediana es
 .
.
Media

Varianza

Desviación típica

Desviación media

Rango

Cuartiles

Deciles
Tenemos que la fórmula para la posición de los deciles está dada por

Por lo tanto, los deciles que buscamos están en las posiciones:

Percentiles
Tenemos que la fórmula para la posición de los percentiles está dada por

Por lo tanto, los percentiles que buscamos están en las posiciones:

Una distribución estadística viene dada por la siguiente tabla:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
Hallar:
a La moda, mediana y media.
b El rango, desviación media y varianza.
c Los cuartiles  y
y  .
.
d Los deciles  y
y  .
.
e Los percentiles  y
y  .
.
Completamos la tabla con:
La frecuencia acumulada ( ) para calcular la mediana.
) para calcular la mediana.
El producto de la variable por su frecuencia absoluta ( ) para calcular la media.
) para calcular la media.
La desviación respecto a la media  y su producto por la frecuencia absoluta
y su producto por la frecuencia absoluta  para calcular la desviación media
para calcular la desviación media
El producto de la variable al cuadrado por su frecuencia absoluta (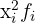 ) para calcular la varianza y la desviación típica
) para calcular la varianza y la desviación típica
 |  |  |  |  | 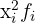 | |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |
Moda
En primer lugar buscamos el intervalo donde se encuentra la moda, que será el intervalo que tenga la mayor frecuencia absoluta ( )
)
La clase modal es: 
Aplicaremos la fórmula para el cálculo de la moda para datos agrupados, extrayendo los siguientes datos:
 .
.
 .
.
 .
.



Mediana
Buscamos el intervalo donde se encuentra la mediana, para ello dividimos la  por
por  porque la mediana es el valor central,
porque la mediana es el valor central,
 .
.
Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
Clase de la mediana:  .
.
Aplicaremos la fórmula para el cálculo de la mediana para datos agrupados, extrayendo los siguientes datos:
 .
.
 .
.
 .
.
 .
.
 .
.
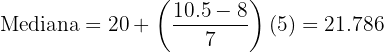 .
.
Media
Calculamos la sumatoria de la variable por su frecuencia absoluta ( ) que es
) que es  y la dividimos por
y la dividimos por 

Desviación media
Calculamos la sumatoria de de los productos de desviaciones respecto a la media por sus frecuencias absolutas correspondientes  que es
que es  y dividimos por
y dividimos por 

Varianza
Calculamos la sumatoria de  , la dividimos por
, la dividimos por  y al resultado le restaremos la media aritmética al cuadrado,
y al resultado le restaremos la media aritmética al cuadrado,  .
.

Desviación típica
Hacemos la raíz cuadrada de la varianza

Cuartiles
Cálculo del primer cuartil
Buscamos el intervalo donde se encuentra el primer cuartil, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos:





Cálculo del tercer cuartil
Buscamos el intervalo donde se encuentra el tercer cuartil, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos:





Deciles
Cálculo del tercer decil
Buscamos el intervalo donde se encuentra el tercer decil, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:





Cálculo del sexto decil
Buscamos el intervalo donde se encuentra el sexto decil, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:





Percentiles
El percentil  es igual al decil
es igual al decil 

Cálculo del percentil 70
Buscamos el intervalo donde se encuentra el percentil  , multiplicando
, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de percentiles para datos agrupados, extrayendo los siguientes datos:





Dada la distribución estadística:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Hallar:
a La mediana y moda.
b Cuartil  y
y  .
.
c Media.
Ampliamos la tabla con otra columna donde disponemos la frecuencia acumulada ( ):
):
En la primera casilla colocamos la primera frecuencia absoluta.
En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente y así sucesivamente hasta la última, que tiene que se igual a  .
.
 |  |  | |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  | |
 |
Moda
En primer lugar buscamos el intervalo donde se encuentra la moda, que será el intervalo que tenga la mayor frecuencia absoluta ( )
)
La clase modal es: 
Aplicaremos la fórmula para el cálculo de la moda para datos agrupados, extrayendo los siguientes datos:
Límite inferior: 





Mediana
Buscamos el intervalo donde se encuentra la mediana, para ello dividimos la  por
por  porque la mediana es el valor central
porque la mediana es el valor central

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
Clase de la mediana: 
Aplicaremos la fórmula para el cálculo de la mediana para datos agrupados, extrayendo los siguientes datos:





Cuartiles
Cálculo del primer cuartil
Buscamos el intervalo donde se encuentra el primer cuartil, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas ( ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos:





Cálculo del tercer cuartil
Buscamos el intervalo donde se encuentra el tercer cuartil, multiplicando  por
por  y dividiendo por
y dividiendo por 

Buscamos en la columna de las frecuencias acumuladas  ) el intervalo que contiene a
) el intervalo que contiene a 
La clase de  es:
es: 
Aplicaremos la fórmula para el cálculo de cuartiles para datos agrupados, extrayendo los siguientes datos:





Media
No se puede calcular la media, porque no se puede hallar la marca de clase del último intervalo.
Si quieres que tus hijos refuercen esta asignatura, no lo dudes y entra Superprof para encontrar clases de matematicas primaria o, si lo prefieres, un profesor de matematicas online.
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en la realización de esta actividad vimos de manera clara toda la distribución de datos. en actividad de las diagramas de barra identificamos las categorías y los intervalos de mayor a menor frecuencia, ya que en la actividad de los polígonos llevamos acabo las tendencias y variables de todo el conjunto de datos. esto son las herramientas que mas utilizamos para hacer la interpretación de datos con la ayuda de ka estadística y hace la comparación de diversos grupos y variables.
Hola excelente resumen de lo que se analiza en el artículo, te felicitamos.
4. La tabla registra el ahorro mensual de s/. 100 mensuales. Completa la tabla y contesta.
a) ¿Cuál es la suma de la tercera y cuarta frecuencia absoluta acumulada?
b) ¿Cuántos estudiantes tienen ahorros mayores o iguales que S/. 20, pero menores que S/. 40?
c) ¿Qué porcentaje de estudiantes tienen ahorros menores que S/. 30?
d) ¿A qué intervalo pertenecen los ahorros de la mayoría de los estudiantes?
Lo unico que no me parecio del ejercicio es que al momento de redondear por ejemplo cuando el resultados es .155 asi fue como lo escribi pero me lo marcaba incorrecto, ya que pedia redondear a 16%
Entonces eso complico un poco a la hora de los resultados.
Hola entendemos tu frustración, pero como a veces sucede que algunos libros o maestros piden redondear y otros no, entonces se tomo este criterio que es mas generalizado.
Hay varios tipos de gráficos