Capítulos
Un diagrama de sectores se puede utilizar para todo tipo de variables, pero se usa frecuentemente para las variables cualitativas.
Los datos se representan en un círculo, de modo que el ángulo de cada sector es proporcional a la frecuencia absoluta correspondiente.
El diagrama circular se construye con la ayuda de un transportador de ángulos.
Ejemplo
En una clase de 30 alumnos, 12 juegan a baloncesto, 3 practican la natación, 9 juegan al fútbol y el resto no practica ningún deporte.
| Alumnos | Ángulo | |
|---|---|---|
| Baloncesto | 12 | 144° |
| Natación | 3 | 36° |
| Fútbol | 9 | 108° |
| Sin deporte | 6 | 72° |
| Total | 30 | 360° |
Diagrama de barras
Un diagrama de barras se utiliza para de presentar datos cualitativos o datos cuantitativos de tipo discreto.
Se representan sobre unos ejes de coordenadas, en el eje de abscisas se colocan los valores de la variable, y sobre el eje de ordenadas las frecuencias absolutas o relativas o acumuladas.
Los datos se representan mediante barras de una altura proporcional a la frecuencia.
Ejemplo
Un estudio hecho al conjunto de los 20 alumnos de una clase para determinar su grupo sanguíneo ha dado el siguiente resultado:
| Grupo sanguíneo | fi |
|---|---|
| A | 6 |
| B | 4 |
| AB | 1 |
| 0 | 9 |
| 20 |
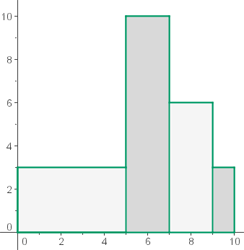
Histograma
Un histograma es una representación gráfica de una variable en forma de barras.
Se utilizan para variables continuas o para variables discretas, con un gran número de datos, y que se han agrupado en clases.
En el eje abscisas se construyen unos rectángulos que tienen por base la amplitud del intervalo, y por altura, la frecuencia absoluta de cada intervalo.
La superficie de cada barra es proporcional a la frecuencia de los valores representados.
Ejemplo
El peso de 65 personas adultas viene dado por la siguiente tabla:
| ci | fi | Fi | |
|---|---|---|---|
| [50, 60) | 55 | 8 | 8 |
| [60, 70) | 65 | 10 | 18 |
| [70, 80) | 75 | 16 | 34 |
| [80, 90) | 85 | 14 | 48 |
| [90, 100) | 95 | 10 | 58 |
| [100, 110) | 110 | 5 | 63 |
| [110, 120) | 115 | 2 | 65 |
| 65 |
Histograma de frecuencias acumuladas
Si se representan las frecuencias acumuladas de una tabla de datos agrupados se obtiene el histograma de frecuencias acumuladas.
Histogramas con intervalos de amplitud diferente
Para costruir un histogramas con intervalo de amplitud diferente tenemos que calcular las alturas de los rectángulos del histograma.
hi es la altura del intervalo
fi es la frecuencia del intervalo
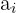ai es la amplitud del intervalo
Ejemplo
En la siguiente tabla se muestra las calificaciones (suspenso, aprobado, notable y sobresaliente) obtenidas pr un grupo de 50 alumnos.
| fi | hi | |
|---|---|---|
| [0, 5) | 15 | 3 |
| [5, 7) | 20 | 10 |
| [7, 9) | 12 | 6 |
| [9, 10) | 3 | 3 |
| 50 |
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en la realización de esta actividad vimos de manera clara toda la distribución de datos. en actividad de las diagramas de barra identificamos las categorías y los intervalos de mayor a menor frecuencia, ya que en la actividad de los polígonos llevamos acabo las tendencias y variables de todo el conjunto de datos. esto son las herramientas que mas utilizamos para hacer la interpretación de datos con la ayuda de ka estadística y hace la comparación de diversos grupos y variables.
Hola excelente resumen de lo que se analiza en el artículo, te felicitamos.
4. La tabla registra el ahorro mensual de s/. 100 mensuales. Completa la tabla y contesta.
a) ¿Cuál es la suma de la tercera y cuarta frecuencia absoluta acumulada?
b) ¿Cuántos estudiantes tienen ahorros mayores o iguales que S/. 20, pero menores que S/. 40?
c) ¿Qué porcentaje de estudiantes tienen ahorros menores que S/. 30?
d) ¿A qué intervalo pertenecen los ahorros de la mayoría de los estudiantes?
Lo unico que no me parecio del ejercicio es que al momento de redondear por ejemplo cuando el resultados es .155 asi fue como lo escribi pero me lo marcaba incorrecto, ya que pedia redondear a 16%
Entonces eso complico un poco a la hora de los resultados.
Hola entendemos tu frustración, pero como a veces sucede que algunos libros o maestros piden redondear y otros no, entonces se tomo este criterio que es mas generalizado.
Hay varios tipos de gráficos