
¿Qué es la media aritmética?
En matemáticas, la media aritmética de una lista de números reales es la suma de los valores divididos por el número de valores. Por ejemplo, si queremos saber la nota media que han sacado los alumnos de una clase, primero sumaremos las calificaciones de todos ellos y después dividiremos entre el número de alumnos de la clase.
Ejercicios resueltos de la media aritmética
Considere los siguientes datos:  .
.
a)Calcula su media.
b)Si todos los datos anteriores los multiplicamos por  . ¿Cuál será la nueva media?
. ¿Cuál será la nueva media?
a)Calcula su media.
La media  de un conjunto de datos está dada por la suma de los datos entre el número total de datos. Así
de un conjunto de datos está dada por la suma de los datos entre el número total de datos. Así

b)Si todos los datos anteriores los multiplicamos por 3. ¿Cuál será la nueva media?

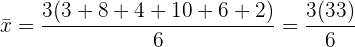
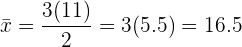
Observamos que, si todos los datos son multiplicados por  , entonces la media aritmética queda multiplicada por
, entonces la media aritmética queda multiplicada por  . Por lo tanto, es posible representar esta observación en la siguiente propiedad que satisface la media aritmética:
. Por lo tanto, es posible representar esta observación en la siguiente propiedad que satisface la media aritmética:
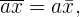
con  una constante.
una constante.
A un conjunto de 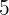 números cuya media es
números cuya media es 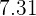 se le añaden los números
se le añaden los números y
y 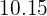 . ¿Cuál es la media del nuevo conjunto de números?
. ¿Cuál es la media del nuevo conjunto de números?
Sabemos de inicio que
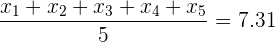
Ahora bien, calculemos la media del conjunto de siete números y desarrollemos de la siguiente manera

Así, la media sigue siendo la misma.
Calcular la media de una distribución estadística que viene dada por la siguiente tabla:
| xi | 61 | 64 | 67 | 70 | 73 |
| fi | 5 | 18 | 42 | 27 | 8 |
La tabla indica a la variable  y al número de veces que se repite en el conjunto de datos
y al número de veces que se repite en el conjunto de datos  , y por esa razón debemos completar la tabla con el producto de la variable por su frecuencia absoluta
, y por esa razón debemos completar la tabla con el producto de la variable por su frecuencia absoluta 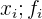 con la finalidad de tener la suma de todos los valores
con la finalidad de tener la suma de todos los valores  que se repiten
que se repiten  veces, y así poder sumar finalmente a todos ellos y dividirlos entre la cantidad de datos que se generó, observe la fórmula
veces, y así poder sumar finalmente a todos ellos y dividirlos entre la cantidad de datos que se generó, observe la fórmula
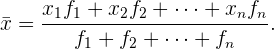
Aquí el desarrollo numérico
| xi | fi | xi · fi |
| 61 | 5 | 305 |
| 64 | 18 | 1152 |
| 67 | 42 | 2814 |
| 71 | 27 | 1890 |
| 73 | 8 | 584 |
| 100 | 6745 |
Entonces solo basta realizar la división

Llegando al resultado deseado.
Hallar la media de la distribución estadística que viene dada por la siguiente tabla:
| fi | |
| [10, 15) | 3 |
| [15, 20) | 5 |
| [20, 25) | 7 |
| [25, 30) | 4 |
| [30, 35) | 2 |
Primero que todo, observemos que ahora los datos no vienen representados de la misma manera que antes, tenemos intervalos de valores. En este caso lo que se realiza es calcular algo llamado marca de clase  . Esto consiste en sacar la media entre los dos valores que definen el intervalo, por ejemplo:
. Esto consiste en sacar la media entre los dos valores que definen el intervalo, por ejemplo:
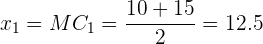
y así sucesivamente con los demás intervalos.
Una vez hecho el cálculo, completamos la tabla con el producto de la variable por su frecuencia absoluta 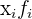 para calcular la media
para calcular la media
| xi | fi | xi · fi | |
| [10, 15) | 12.5 | 3 | 37.5 |
| [15, 20) | 17.5 | 5 | 87.5 |
| [20, 25) | 22.5 | 7 | 157.5 |
| [25, 30) | 27.5 | 4 | 110 |
| [30, 35) | 32.5 | 2 | 65 |
| 21 | 457.5 |
Calculamos la sumatoria de la variable por su frecuencia absoluta 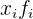 que es
que es 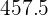 y la dividimos entre el total de datos
y la dividimos entre el total de datos 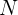 que es
que es 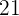 . Así
. Así
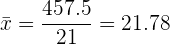
Los resultados al lanzar un dado 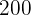 veces vienen dados por la siguiente tabla
veces vienen dados por la siguiente tabla
| 1 | 2 | 3 | 4 | 5 | 6 | |
| fi | a | 32 | 35 | 33 | b | 35 |
Determinar  y
y  sabiendo que la puntuación media es
sabiendo que la puntuación media es  .
.
De los datos dados podemos construir la siguiente tabla
| xi | fi | xi · fi |
| 1 | a | a |
| 2 | 32 | 64 |
| 3 | 35 | 125 |
| 4 | 33 | 132 |
| 5 | b | 5b |
| 6 | 35 | 210 |
| 135 + a + b | 511 + a + 5b |
La suma de los datos de la columna  nos da
nos da

Lo anterior lo igualamos a 200 que es una de las hipótesis del problema. Así
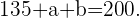
Simplificando obtenemos nuestra primer ecuación
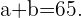
Ahora calculamos la media de la distribución y la igualamos a 3.6 que es el valor que nos indica el problema
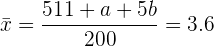
Nuevamente simplificando obtenemos nuestra segunda ecuación

Por lo tanto tenemos el siguiente sistema de ecuaciones

Lo resolvemos por el método de reducción
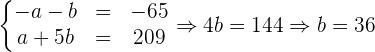 .
.
Por lo tanto
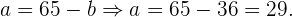
Así concluimos que
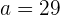 y
y 
Calcular la media de la distribución estadística:
| fi | |
| [0, 5) | 3 |
| [5, 10) | 5 |
| [10, 15) | 7 |
| [15, 20) | 8 |
| [20, 25) | 2 |
| [25, ∞) | 6 |
Comenzamos calculando la 
| xi | fi | |
| [0, 5) | 2.5 | 3 |
| [5, 10) | 7.5 | 5 |
| [10, 15) | 12.5 | 7 |
| [15, 20) | 17.5 | 8 |
| [20, 25) | 22.5 | 2 |
| [25, ∞) | --- | 6 |
| 31 |
Y aquí observamos que NO se puede calcular la media porque no se puede hallar la marca de clase del último intervalo.
Considere los siguientes datos: 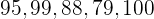 .
.
a)Calcula su media.
b)Si a todos los datos anteriores le sumanos 6. ¿Cuál será la nueva media?
a)Calcula su media.
La media  de un conjunto de datos está dada por la suma de los datos entre el número total de datos. Así
de un conjunto de datos está dada por la suma de los datos entre el número total de datos. Así

b)Si a todos los datos anteriores le sumamos  . ¿Cuál será la nueva media?
. ¿Cuál será la nueva media?

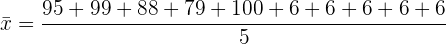

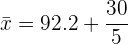
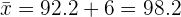
Observamos que, si a todos los datos le sumamos  , entonces la media aritmética queda sumada por
, entonces la media aritmética queda sumada por  . Por lo tanto, es posible representar esta observación en la siguiente propiedad que satisface la media aritmética:
. Por lo tanto, es posible representar esta observación en la siguiente propiedad que satisface la media aritmética:
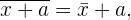
con  una constante.
una constante.
Las alturas en cm de los  jugadores que iniciaron un partido de vóleibol, separados por equipo, son las siguientes:
jugadores que iniciaron un partido de vóleibol, separados por equipo, son las siguientes:
Equipo 1: 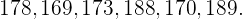
Equipo 2: 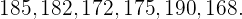
a)Calcula la media de cada equipo.
b)Calcula la media del partido.
a)Calcula la media de cada equipo.
Equipo 1:

Equipo 2:
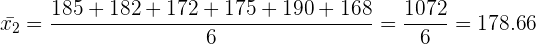
b)Calcula la media del partido.
Para calcular la media del partido,  , calculamos la media de las medias
, calculamos la media de las medias  y
y 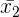 . Así,
. Así,
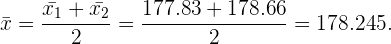
La mediana de un conjunto de  datos es de
datos es de 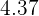 . Si se añaden
. Si se añaden  datos, uno de los cuales es
datos, uno de los cuales es 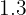 , ¿qué valor debe tener el segundo dato para que la media se mantenga?
, ¿qué valor debe tener el segundo dato para que la media se mantenga?
Para que la media del conjunto de datos se mantenga, los dos datos añadidos deben satisfacer que su media sea igual a 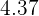 . Tenemos el conocimiento de que uno de ellos es
. Tenemos el conocimiento de que uno de ellos es 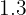 . Llamemos al segundo dato "
. Llamemos al segundo dato " ". Por lo tanto, lo que se busca es que
". Por lo tanto, lo que se busca es que

Resolvemos esta ecuación de primer grado:
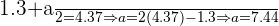
Así, el segundo dato debe de ser  . Como podemos comprobar sencillamente, la media sigue siendo
. Como podemos comprobar sencillamente, la media sigue siendo 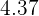 :
:

Calcula la media de los primeros  múltiplos de
múltiplos de  . Generaliza el resultado anterior para calcular la media de los primeros
. Generaliza el resultado anterior para calcular la media de los primeros  múltiplos de
múltiplos de  .
.
Los primeros  múltiplos de
múltiplos de  son:
son:
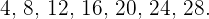
Así, su media es
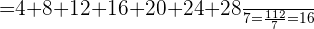
Para generalizar el resultado anterior, nótese que, el n-ésimo múltiplo de  es
es 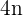 . Así, la media es
. Así, la media es

Tomando el valor  en la expresión de arriba, obtenemos el resultado al primer apartado del ejercicio.
en la expresión de arriba, obtenemos el resultado al primer apartado del ejercicio.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me gusto la dinámica solo que no pude completar lo ultimo
Hola nos alegra que te halla gustado la dinámica, si tienes una duda con confianza coméntalo y te responderemos.
en la realización de esta actividad vimos de manera clara toda la distribución de datos. en actividad de las diagramas de barra identificamos las categorías y los intervalos de mayor a menor frecuencia, ya que en la actividad de los polígonos llevamos acabo las tendencias y variables de todo el conjunto de datos. esto son las herramientas que mas utilizamos para hacer la interpretación de datos con la ayuda de ka estadística y hace la comparación de diversos grupos y variables.
Hola excelente resumen de lo que se analiza en el artículo, te felicitamos.
4. La tabla registra el ahorro mensual de s/. 100 mensuales. Completa la tabla y contesta.
a) ¿Cuál es la suma de la tercera y cuarta frecuencia absoluta acumulada?
b) ¿Cuántos estudiantes tienen ahorros mayores o iguales que S/. 20, pero menores que S/. 40?
c) ¿Qué porcentaje de estudiantes tienen ahorros menores que S/. 30?
d) ¿A qué intervalo pertenecen los ahorros de la mayoría de los estudiantes?
Lo unico que no me parecio del ejercicio es que al momento de redondear por ejemplo cuando el resultados es .155 asi fue como lo escribi pero me lo marcaba incorrecto, ya que pedia redondear a 16%
Entonces eso complico un poco a la hora de los resultados.
Hola entendemos tu frustración, pero como a veces sucede que algunos libros o maestros piden redondear y otros no, entonces se tomo este criterio que es mas generalizado.