¡Bienvenido a nuestra página dedicada a ejercicios resueltos de la mediana! Si estás buscando mejorar tus habilidades en estadísticas y comprender mejor uno de los conceptos fundamentales, has llegado al lugar adecuado.
La mediana es una medida estadística fundamental que nos proporciona información valiosa sobre el valor central de un conjunto de datos, independientemente de los valores extremos.
En este artículo, resolveremos ejercicios sobre el cálculo de la mediana. Estos ejercicios están diseñados especialmente para ti. Ya sea que estés estudiando matemáticas, preparándote para un examen o simplemente buscando ampliar tus conocimientos, nuestros ejercicios te brindarán la práctica necesaria para convertirte en un experto en el cálculo y la interpretación de la mediana. ¡Prepárate para sumergirte en números y datos!
Hallar la mediana de las siguientes series de números:
a)
b)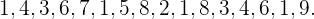
a) Primero, ordenamos los números de menos a mayor:
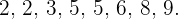
Como la serie de números tiene un número par de estos, entonces su mediana es la media (o promedio) entre las dos puntuaciones centrales. Así,
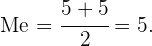
b) Primero, ordenamos los números de menos a mayor:
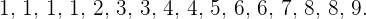
Como la serie de números tiene un número par de estos, entonces su mediana es la media (o promedio) entre las dos puntuaciones centrales. Así,
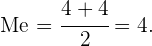
Hallar la mediana de las siguientes series de números:
a)
b)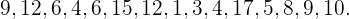
a) Primero, ordenamos los números de menos a mayor:
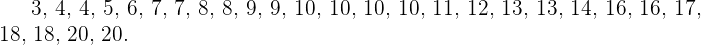
Como la serie de números tiene un número impar de estos, entonces su mediana es la puntuación central. Así,

b) Primero, ordenamos los números de menos a mayor:
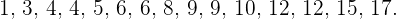
Como la serie de números tiene un número par de estos, entonces su mediana es la puntuación central. Así,
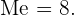
Tabular y calcular mediana de la siguiente serie de números:
 .
.
Comenzamos creando nuestra tabla:
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |
Para calcular la media, dividimos el total de elementos en nuestra serie,  entre
entre  . Esto resulta
. Esto resulta
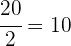
Ahora, ubicamos la casilla de las  donde se encuentra el número
donde se encuentra el número  . Esto corresponde a
. Esto corresponde a  . Así
. Así

Hallar la mediana de la distribución estadística que viene dada por la siguiente tabla:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
Comenzamos añadiendo otra columna en la tabla la cual corresonderá a la frecuencia acumulada,  .
.
Para crearla, comenzamos colocando en la primera casilla la primera frecuencia absoluta. En la segunda casilla, sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente. Continuamos con este proceso hasta la última casilla que debe ser llenada con el número total de datos, 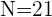 . Así, la tabla queda de la siguiente forma:
. Así, la tabla queda de la siguiente forma:
 |  | |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
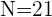 |
Ahora, buscamos el intervalo en donde se encuentra la mediana. Para ello, dividimos a  entre
entre  ya que la mediana corresponde al valor central. Así, obtenemos que
ya que la mediana corresponde al valor central. Así, obtenemos que

Ubicamos el intervalo que contiene a  en la columna de las frecuencias acumuladas,
en la columna de las frecuencias acumuladas,  . Este intervalo es
. Este intervalo es 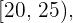 el cual es llamado la clase de la mediana
el cual es llamado la clase de la mediana
Ahora, aplicaremos la fórmula para el cálculo de la mediana para datos agrupados,
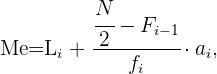
identificando que

Aquí, 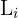 y
y 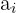 corrresponden a el límite inferior de la clase donde se encuentra la mediana y a la amplitud de la clase, respectivamente. Así
corrresponden a el límite inferior de la clase donde se encuentra la mediana y a la amplitud de la clase, respectivamente. Así
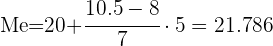
Calcular la mediana de las alturas de los jugadores de un equipo de baloncesto que vienen dadas por la tabla:
| Altura | Nº de jugadores |
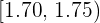 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Comenzamos añadiendo otra columna en la tabla la cual corresonderá a la frecuencia acumulada,  .
.
Para crearla, comenzamos colocando en la primera casilla la primera frecuencia absoluta. En la segunda casilla, sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente. Continuamos con este proceso hasta la última casilla que debe ser llenada con el número total de datos, 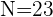 . Así, la tabla queda de la siguiente forma:
. Así, la tabla queda de la siguiente forma:
 |  | |
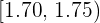 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |
Ahora, buscamos el intervalo en donde se encuentra la mediana. Para ello, dividimos a  entre
entre  ya que la mediana corresponde al valor central. Así, obtenemos que
ya que la mediana corresponde al valor central. Así, obtenemos que
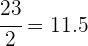
Ubicamos el intervalo que contiene a  en la columna de las frecuencias acumuladas,
en la columna de las frecuencias acumuladas,  . Este intervalo es
. Este intervalo es 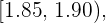 el cual es llamado la clase de la mediana
el cual es llamado la clase de la mediana
Ahora, aplicaremos la fórmula para el cálculo de la mediana para datos agrupados,
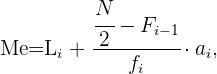
identificando que
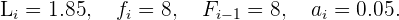
Aquí, 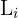 y
y 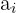 corrresponden a el límite inferior de la clase donde se encuentra la mediana y a la amplitud de la clase, respectivamente. Así
corrresponden a el límite inferior de la clase donde se encuentra la mediana y a la amplitud de la clase, respectivamente. Así

Un dado fue tirado  veces y los resultados fueron los siguientes:
veces y los resultados fueron los siguientes:

a)Hallar su mediana
b)Si multiplicamos cada dato por  , ¿cuál es su mediana?
, ¿cuál es su mediana?
a) Primero, ordenamos los números de menos a mayor:
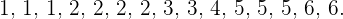
Como la serie de números tiene un número impar de estos, entonces su mediana es la puntuación central. Así,
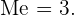
b) Utilizamos la serie de números ya ordenada de arriba y la multiplicamos por  :
:
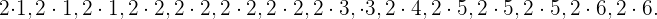
Así, la nueva serie de números es:
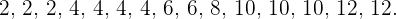
Ahora, como la serie de números tiene igualmente un número impar de estos, entonces su mediana es la puntuación central. Así,

Notemos que, si  , representa la mediana del conjunto de datos original del apartado a), y
, representa la mediana del conjunto de datos original del apartado a), y  , representa la mediana del conjunto de datos que hemos multiplicado por
, representa la mediana del conjunto de datos que hemos multiplicado por  , entonces
, entonces
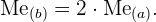
Esto es cierto en general, es decir, si  es un conjunto finito de datos,
es un conjunto finito de datos,  es cualquier número real, y si
es cualquier número real, y si 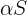 representa multiplicar cada dato del conjunto por
representa multiplicar cada dato del conjunto por  , entonces se tiene que
, entonces se tiene que

Las calificaciones finales de  estudiantes que tomaron la clase de historia fueron las siguientes:
estudiantes que tomaron la clase de historia fueron las siguientes:
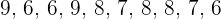
a)Hallar la mediana del conjunto de calificaciones.
b)Si el profesor decidió otorgarles  punto extra a cada estudiante, ¿cuál es ahora la mediana del conjunto de calificaciones?
punto extra a cada estudiante, ¿cuál es ahora la mediana del conjunto de calificaciones?
a) Primero, ordenamos los números de menos a mayor:

Como la serie de números tiene un número par de estos, entonces su mediana es la media (o promedio) entre las dos puntuaciones centrales. Así,
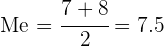
b) Utilizamos la serie de números ya ordenada de arriba y le sumamos  a cada dato:
a cada dato:
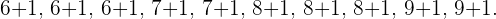
Así, la nueva serie de números es:
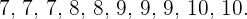
Ahora, como la serie de números tiene igualmente un número par de estos, entonces su mediana, nuevamente, es la media (o promedio) de las dos puntuaciones centrales. Así,

Notemos que, si  , representa la mediana del conjunto de datos original del apartado a), y
, representa la mediana del conjunto de datos original del apartado a), y  , representa la mediana del conjunto de datos al que le hemos sumado
, representa la mediana del conjunto de datos al que le hemos sumado  , entonces
, entonces
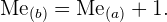
Esto es cierto en general, es decir, si  es un conjunto finito de datos,
es un conjunto finito de datos,  es cualquier número real, y si
es cualquier número real, y si 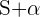 representa sumar
representa sumar  a cada dato del conjunto, entonces se tiene que
a cada dato del conjunto, entonces se tiene que
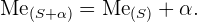
Calcular la mediana de las edades de mujeres que dieron a luz en el mes de Julio en una hospital, las cuales vienen dadas por la siguiente tabla:
| Edad | Nº de mujeres |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Comenzamos añadiendo otra columna en la tabla la cual corresonderá a la frecuencia acumulada,  .
.
Para crearla, comenzamos colocando en la primera casilla la primera frecuencia absoluta. En la segunda casilla, sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente. Continuamos con este proceso hasta la última casilla que debe ser llenada con el número total de datos, 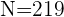 . Así, la tabla queda de la siguiente forma:
. Así, la tabla queda de la siguiente forma:
 |  | |
 |  |  |
 |  | 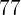 |
 |  |  |
 |  | 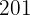 |
 |  |  |
 |  |  |
 |
Ahora, buscamos el intervalo en donde se encuentra la mediana. Para ello, dividimos a  entre
entre  ya que la mediana corresponde al valor central. Así, obtenemos que
ya que la mediana corresponde al valor central. Así, obtenemos que
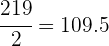
Ubicamos el intervalo que contiene a 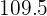 en la columna de las frecuencias acumuladas,
en la columna de las frecuencias acumuladas,  . Este intervalo es
. Este intervalo es 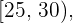 el cual es llamado la clase de la mediana
el cual es llamado la clase de la mediana
Ahora, aplicaremos la fórmula para el cálculo de la mediana para datos agrupados,
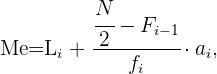
identificando que
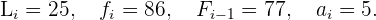
Aquí, 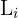 y
y 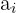 corrresponden a el límite inferior de la clase donde se encuentra la mediana y a la amplitud de la clase, respectivamente. Así
corrresponden a el límite inferior de la clase donde se encuentra la mediana y a la amplitud de la clase, respectivamente. Así

Calcular la mediana de las temperaturas que se registraron en una ciudad del año pasado, las cuales vienen dadas por la siguiente tabla:
| Temperatura en C° | Nº de días |
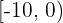 |  |
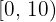 |  |
 |  |
 | 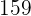 |
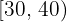 |  |
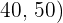 |  |
Comenzamos añadiendo otra columna en la tabla la cual corresonderá a la frecuencia acumulada,  .
.
Para crearla, comenzamos colocando en la primera casilla la primera frecuencia absoluta. En la segunda casilla, sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente. Continuamos con este proceso hasta la última casilla que debe ser llenada con el número total de datos,  . Así, la tabla queda de la siguiente forma:
. Así, la tabla queda de la siguiente forma:
 |  | |
 |  |  |
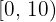 |  |  |
 |  | 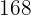 |
 | 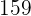 | 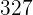 |
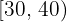 |  | 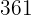 |
 |  |  |
 |
Ahora, buscamos el intervalo en donde se encuentra la mediana. Para ello, dividimos a  entre
entre  ya que la mediana corresponde al valor central. Así, obtenemos que
ya que la mediana corresponde al valor central. Así, obtenemos que
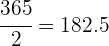
Ubicamos el intervalo que contiene a  en la columna de las frecuencias acumuladas,
en la columna de las frecuencias acumuladas,  . Este intervalo es
. Este intervalo es 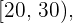 el cual es llamado la clase de la mediana
el cual es llamado la clase de la mediana
Ahora, aplicaremos la fórmula para el cálculo de la mediana para datos agrupados,
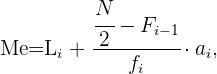
identificando que

Aquí, 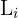 y
y 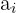 corrresponden a el límite inferior de la clase donde se encuentra la mediana y a la amplitud de la clase, respectivamente. Así
corrresponden a el límite inferior de la clase donde se encuentra la mediana y a la amplitud de la clase, respectivamente. Así
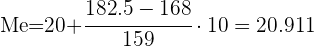
Tabular y calcular mediana de la siguiente serie de números:
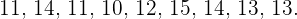 .
.
Comenzamos creando nuestra tabla:
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |
Para calcular la media, dividimos el total de elementos en nuestra serie, 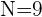 entre
entre  . Esto resulta
. Esto resulta
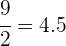
Ahora, ubicamos la casilla de las  donde se encuentra el número
donde se encuentra el número  . Esto corresponde a
. Esto corresponde a  . Así
. Así
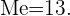
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en la realización de esta actividad vimos de manera clara toda la distribución de datos. en actividad de las diagramas de barra identificamos las categorías y los intervalos de mayor a menor frecuencia, ya que en la actividad de los polígonos llevamos acabo las tendencias y variables de todo el conjunto de datos. esto son las herramientas que mas utilizamos para hacer la interpretación de datos con la ayuda de ka estadística y hace la comparación de diversos grupos y variables.
Hola excelente resumen de lo que se analiza en el artículo, te felicitamos.
4. La tabla registra el ahorro mensual de s/. 100 mensuales. Completa la tabla y contesta.
a) ¿Cuál es la suma de la tercera y cuarta frecuencia absoluta acumulada?
b) ¿Cuántos estudiantes tienen ahorros mayores o iguales que S/. 20, pero menores que S/. 40?
c) ¿Qué porcentaje de estudiantes tienen ahorros menores que S/. 30?
d) ¿A qué intervalo pertenecen los ahorros de la mayoría de los estudiantes?
Lo unico que no me parecio del ejercicio es que al momento de redondear por ejemplo cuando el resultados es .155 asi fue como lo escribi pero me lo marcaba incorrecto, ya que pedia redondear a 16%
Entonces eso complico un poco a la hora de los resultados.
Hola entendemos tu frustración, pero como a veces sucede que algunos libros o maestros piden redondear y otros no, entonces se tomo este criterio que es mas generalizado.
Hay varios tipos de gráficos