Capítulos

Definición de distribución de frecuencias
La distribución de frecuencias o tabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente.
Tipos de frecuencias
Frecuencia absoluta
La frecuencia absoluta es el número de veces que aparece un determinado valor en un estudio estadístico.
Al tirar una moneda  veces salen
veces salen  caras
caras
Se representa por  , aunque otros autores la representan como
, aunque otros autores la representan como  .
.
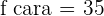

La suma de las frecuencias absolutas es igual al número total de datos, que se representa por  .
.
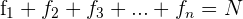

Para indicar resumidamente estas sumas se utiliza la letra griega 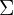 (sigma mayúscula) que se lee suma o sumatoria.
(sigma mayúscula) que se lee suma o sumatoria.
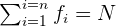
Frecuencia relativa
La frecuencia relativa es el cociente entre la frecuencia absoluta de un determinado valor y el número total de datos.
Se puede expresar en tanto por ciento y se representa por  .
.
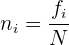
La frecuencia relativa es un número comprendido entre  y
y  .
.
La suma de las frecuencias relativas es igual a  .
.
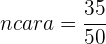
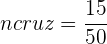
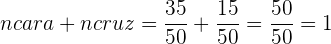
Frecuencia acumulada
La frecuencia acumulada es la suma de las frecuencias absolutas de todos los valores inferiores o iguales al valor considerado.
Se representa por  .
.
Frecuencia relativa acumulada
La frecuencia relativa acumulada es el cociente entre la frecuencia acumulada de un determinado valor y el número total de datos.
Se puede expresar en tantos por ciento.
Ejemplo:
Durante el mes de julio, en una ciudad se han registrado las siguientes temperaturas máximas:
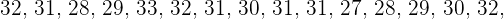
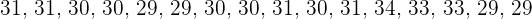 .
.
En la primera columna de la tabla colocamos la variable ordenada de menor a mayor
En la segunda hacemos el recuento
En la tercera anotamos la frecuencia absoluta
En la cuarta anotamos la frecuencia acumulada:
En la primera casilla colocamos la primera frecuencia absoluta:
En la segunda casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente:
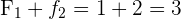
En la tercera casilla sumamos el valor de la frecuencia acumulada anterior más la frecuencia absoluta correspondiente:

La última tiene que ser igual a  (sumatoria de
(sumatoria de  ).
).
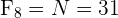
En la quinta columna disponemos las frecuencias relativas 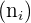 que son el resultado de dividir cada frecuencia absoluta por
que son el resultado de dividir cada frecuencia absoluta por 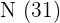
En la sexta anotamos la frecuencia relativa acumulada  .
.
En la primera casilla colocamos la primera frecuencia relativa acumulada.
En la segunda casilla sumamos el valor de la frecuencia relativa acumulada anterior más la frecuencia relativa correspondiente y así sucesivamente hasta la última, que tiene que ser igual a  .
.
 | Recuento |  |  |  |  |
|---|---|---|---|---|---|
 | I |  |  |  |  |
 | II |  |  | 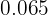 |  |
 |  |  |  |  | |
 |  |  |  |  | |
 |  |  |  |  | |
 | III |  |  |  |  |
 | III |  |  |  |  |
 | I |  |  |  |  |
 |  |
Este tipo de tablas de frecuencias se utiliza con variables discretas.
Distribución de frecuencias agrupadas
La distribución de frecuencias agrupadas o tabla con datos agrupados se emplea si las variables toman un número grande de valores o la variable es continua.
Se agrupan los valores en intervalos que tengan la misma amplitud denominados clases. A cada clase se le asigna su frecuencia correspondiente.
Límites de la clase
Cada clase está delimitada por el límite inferior de la clase y el límite superior de la clase.
Amplitud de la clase
La amplitud de la clase es la diferencia entre el límite superior e inferior de la clase.
Marca de clase
La marca de clase es el punto medio de cada intervalo y es el valor que representa a todo el intervalo para el cálculo de algunos parámetros.
La marca de clase se representa por 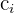
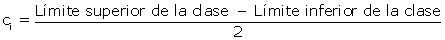
Construcción de una tabla de datos agrupados
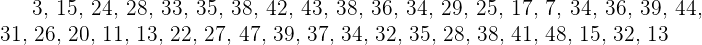 .
.
1º Se localizan los valores menor y mayor de la distribución. En este caso son  y
y  .
.
2º Se restan y se busca un número entero un poco mayor que la diferencia y que sea
divisible por el número de intervalos queramos establecer.
Es conveniente que el número de intervalos oscile entre  y
y  .
.
En este caso, 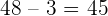 , incrementamos el número hasta
, incrementamos el número hasta  ,
, 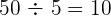 intervalos.
intervalos.
Se forman los intervalos teniendo presente que el límite inferior de una clase pertenece al intervalo, pero el límite superior no pertenece intervalo, se cuenta en el siguiente intervalo.
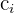 es la marca de clase que es el punto medio de cada intervalo.
es la marca de clase que es el punto medio de cada intervalo.
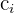 |  |  |  |  | |
|---|---|---|---|---|---|
 |  |  |  |  |  |
 |  |  |  |  | 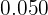 |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  | 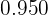 |
 |  |  |  | 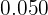 |  |
 | 1 |
Si siguen teniendo dudas con la construcción de tablas de frecuencias, busca un profesor particular matematicas en Superprof. ¡Estaremos encantados de ayudarte!
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en la realización de esta actividad vimos de manera clara toda la distribución de datos. en actividad de las diagramas de barra identificamos las categorías y los intervalos de mayor a menor frecuencia, ya que en la actividad de los polígonos llevamos acabo las tendencias y variables de todo el conjunto de datos. esto son las herramientas que mas utilizamos para hacer la interpretación de datos con la ayuda de ka estadística y hace la comparación de diversos grupos y variables.
Hola excelente resumen de lo que se analiza en el artículo, te felicitamos.
4. La tabla registra el ahorro mensual de s/. 100 mensuales. Completa la tabla y contesta.
a) ¿Cuál es la suma de la tercera y cuarta frecuencia absoluta acumulada?
b) ¿Cuántos estudiantes tienen ahorros mayores o iguales que S/. 20, pero menores que S/. 40?
c) ¿Qué porcentaje de estudiantes tienen ahorros menores que S/. 30?
d) ¿A qué intervalo pertenecen los ahorros de la mayoría de los estudiantes?
Lo unico que no me parecio del ejercicio es que al momento de redondear por ejemplo cuando el resultados es .155 asi fue como lo escribi pero me lo marcaba incorrecto, ya que pedia redondear a 16%
Entonces eso complico un poco a la hora de los resultados.
Hola entendemos tu frustración, pero como a veces sucede que algunos libros o maestros piden redondear y otros no, entonces se tomo este criterio que es mas generalizado.
Hay varios tipos de gráficos