Los deciles son medidas estadísticas que dividen un conjunto de datos ordenados en diez partes iguales, lo que permite analizar la distribución de los valores dentro de una muestra o población. En total existen nueve deciles que marcan los valores por debajo de los cuales se encuentra el 10 %, 20 %, ..., hasta el 90 % de los datos.
Los deciles se utilizan con frecuencia en áreas como la economía, la educación y la investigación social, ya que permiten interpretar con mayor detalle la dispersión y la posición de los datos, especialmente en estudios de rendimiento o ingresos.
En este artículo te presentamos ejercicios resueltos paso a paso que te permitirán aprender a calcular deciles correctamente, interpretar su significado y aplicarlos en distintos contextos estadísticos.
Resuelve los siguientes ejercicios:
Dadas las series estadísticas:
Calcular los deciles 2 y 7.
Realizamos el cálculo para la primera serie, para ello primero ordenamos los datos de menor a mayor: 
Aplicamos la fórmula para obtener la posición del decil 2
El decil 2 es aquel que se encuentra en la posición 2. Así 
Aplicamos la fórmula para obtener la posición del decil 7
El decil 7 es aquel que se encuentra en la posición 5. Así 
Realizamos el cálculo para la segunda serie, para ello primero ordenamos los datos de menor a mayor: 
Aplicamos la fórmula para obtener la posición del decil 2
El decil 2 es aquel que se encuentra en la posición 2. Así 
Aplicamos la fórmula para obtener la posición del decil 7
El decil 7 es aquel que se encuentra en la posición 6. Así
Calcular los deciles de la distribución de la tabla:
 |  | |
|---|---|---|
 |  | |
 |  |  |
 |  |  |
 |  |  |
 | |  |
 |  |  |
 |  |  |
|
Cálculo del primer decil
Buscamos el intervalo donde se encuentra el primer decil, multiplicando 
por 
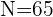y dividiendo por 
Buscamos en la columna de las frecuencias acumuladas 
el intervalo que contiene a 
La clase de 
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:
Cálculo del segundo decil
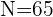Buscamos el intervalo donde se encuentra el segundo decil, multiplicando por y dividiendo por
Buscamos en la columna de las frecuencias acumuladas el intervalo que contiene a 
La clase de 
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:
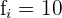
Cálculo del tercer decil
Cálculo del cuarto decil
Cálculo del quinto decil
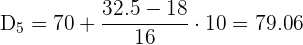
Cálculo del sexto decil
Cálculo del séptimo decil
Cálculo del octavo decil
Cálculo del noveno decil
Una distribución estadística viene dada por la siguiente tabla:
 | |
 |  |
 | |
 |  |
 |  |
 | |
Hallar los deciles 3 y 6 .
Completamos la tabla con a frecuencia acumulada:
 | | | |
|  | | |
|  | | |
|  | |  |
|  | |  |
|  | |  |
|
Cálculo del tercer decil
Buscamos el intervalo donde se encuentra el tercer decil, multiplicando por 
y dividiendo por
Buscamos en la columna de las frecuencias acumuladas el intervalo que contiene a 
La clase de 
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:
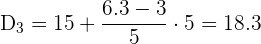
Cálculo del sexto decil
Buscamos el intervalo donde se encuentra el sexto decil, multiplicando 
por y dividiendo por
Buscamos en la columna de las frecuencias acumuladas el intervalo que contiene a 
La clase de 
es: 
Aplicaremos la fórmula para el cálculo de deciles para datos agrupados, extrayendo los siguientes datos:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en la realización de esta actividad vimos de manera clara toda la distribución de datos. en actividad de las diagramas de barra identificamos las categorías y los intervalos de mayor a menor frecuencia, ya que en la actividad de los polígonos llevamos acabo las tendencias y variables de todo el conjunto de datos. esto son las herramientas que mas utilizamos para hacer la interpretación de datos con la ayuda de ka estadística y hace la comparación de diversos grupos y variables.
Hola excelente resumen de lo que se analiza en el artículo, te felicitamos.
4. La tabla registra el ahorro mensual de s/. 100 mensuales. Completa la tabla y contesta.
a) ¿Cuál es la suma de la tercera y cuarta frecuencia absoluta acumulada?
b) ¿Cuántos estudiantes tienen ahorros mayores o iguales que S/. 20, pero menores que S/. 40?
c) ¿Qué porcentaje de estudiantes tienen ahorros menores que S/. 30?
d) ¿A qué intervalo pertenecen los ahorros de la mayoría de los estudiantes?
Lo unico que no me parecio del ejercicio es que al momento de redondear por ejemplo cuando el resultados es .155 asi fue como lo escribi pero me lo marcaba incorrecto, ya que pedia redondear a 16%
Entonces eso complico un poco a la hora de los resultados.
Hola entendemos tu frustración, pero como a veces sucede que algunos libros o maestros piden redondear y otros no, entonces se tomo este criterio que es mas generalizado.
Hay varios tipos de gráficos