Capítulos
Bienvenidos a nuestra sección dedicada a Ejercicios de Desviación Media. La desviación media es una medida estadística que nos proporciona una comprensión cuantitativa de la dispersión o variabilidad de un conjunto de datos con respecto a su media aritmética. En esta serie de ejercicios, exploraremos diversos escenarios y conjuntos de datos para calcular y comprender la desviación media.
A lo largo de estos problemas, te enfrentarás a situaciones prácticas y datos concretos, permitiéndote aplicar de manera efectiva el concepto de desviación media. Este concepto es crucial en estadística, ya que nos brinda información sobre la dispersión promedio de los datos con respecto a la media, lo que es esencial para comprender la variabilidad en conjuntos de información del mundo real.
A medida que abordes estos ejercicios, desarrollarás habilidades para calcular la desviación media, interpretar sus resultados y aplicar este conocimiento en diversos contextos. Prepárate para explorar la variabilidad en conjuntos de datos y mejorar tus habilidades analíticas en estadística.
Desviación media de series de números
Hallar la desviación media de la serie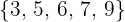 
Pimero calculamos la media
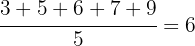
Ahora calculamos la desviación media
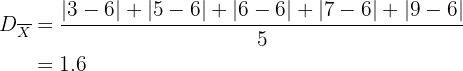
Hallar la desviación media de la serie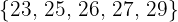 
Pimero calculamos la media
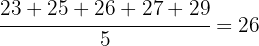
Ahora calculamos la desviación media
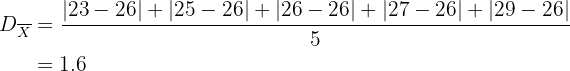
Hallar la desviación media de las series de números siguientes:
a 
.
b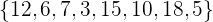 
.
c 
.
a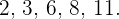 
Media:
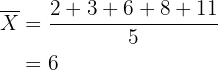
Desviación media:
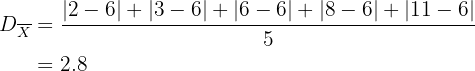
b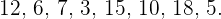 
Media:
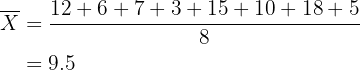
Desviación media:
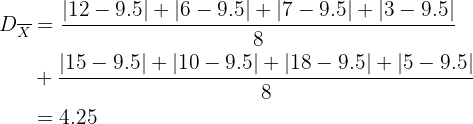
c .
Media:
.
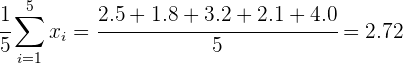Desviación Media:
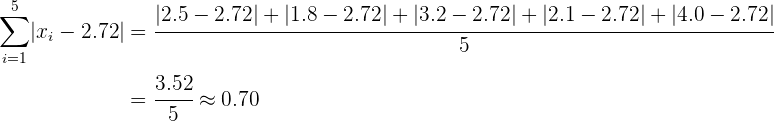
Cambiando un valor en el conjunto
Encuentra la media y desviación media del conjunto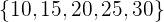 
. Después, reemplaza el valor de 15 por el valor de 30, para obtener el conjunto 
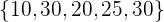. Calcula la media y desviación media, y compara con la previamente obtenida.
Primero calculamos la media y desviación media del primer conjunto
Media:
.
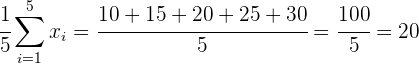Desviación Media:
.
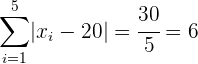Ahora, lo hacemos con el segundo conjunto:
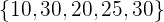
Media:
.
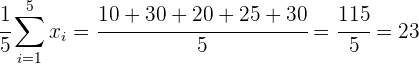Desviación Media:
.
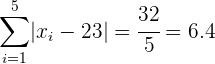Entonces, a pesar de que reemplazar el 15 por el 30 parece que estabilizamos el conjunto, en realidad estamos aumentando la desviación media por el hecho de aún tener ese 10.
Encuentra la media y desviación media del conjunto 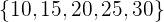. Después, reemplaza el valor de 15 por el valor de 20, para obtener el conjunto 
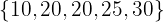. Calcula la media y desviación media, y compara con la previamente obtenida.
Primero calculamos la media y desviación media del primer conjunto
Media:
.
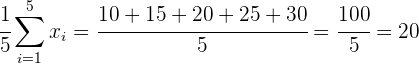Desviación Media:
.
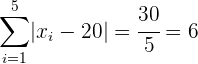Ahora, lo hacemos con el segundo conjunto:
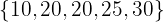
Media:
.
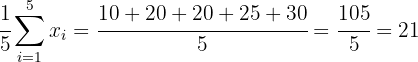Desviación Media:
.
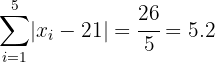Entonces, a pesar de que reemplazar el 15 por el 20 parece que estabilizamos el conjunto, en realidad estamos disminuyendo la desviación media por el hecho de aún tener ese 10.
Encuentra la media y desviación media del conjunto 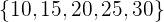. Después, reemplaza el valor de 10 y 15 por el valor de 30, para obtener el conjunto 
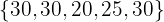. Calcula la media y desviación media, y compara con la previamente obtenida.
Primero calculamos la media y desviación media del primer conjunto
Media:
.
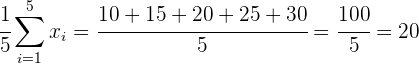Desviación Media:
.
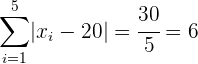Ahora, lo hacemos con el segundo conjunto:
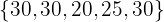
Media:
.
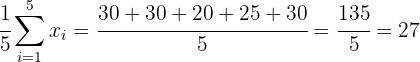Desviación Media:
.
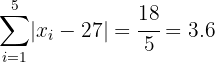Entonces, a pesar de que reemplazar el 10 y 15 por el 30 parece que estabilizamos el conjunto, en realidad estamos disminuyendo la desviación media.
Efectos de transformar el conjunto
Sea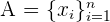 
un conjunto de número. ¿Qué ocurre con la desviación media de A si a cada uno de sus elementos le sumamos 
?
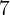Sea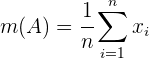 
la media de 
. Entonces, su desviación media es 
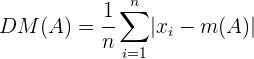
Ahora, notemos que al hacer la modificación del conjunto , obtenemos el conjunto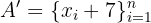 
cuya media es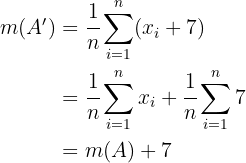
Ahora, la nueva desviación media es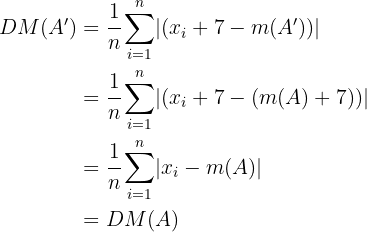 
Es decir, la desviación media es invariante bajo traslaciones del conjunto.
Sea 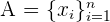un conjunto de número. ¿Qué ocurre con la desviación media de A si a cada uno de sus elementos le sumamos un número fijo 
?
Sea
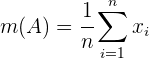
la media de . Entonces, su desviación media es
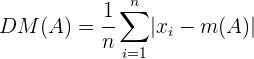
Ahora, notemos que al hacer la modificación del conjunto , obtenemos el conjunto
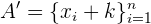
cuya media es
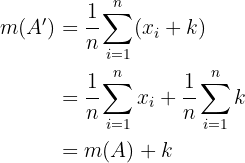
Ahora, la nueva desviación media es
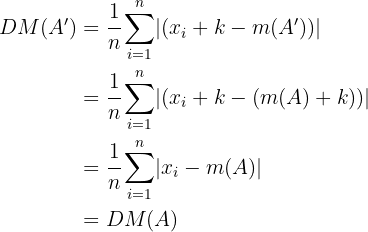
Es decir, la desviación media es invariante bajo traslaciones del conjunto.
Sea 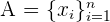un conjunto de número. ¿Qué ocurre con la desviación media de A si a cada uno de sus elementos le multiplicamos un número fijo ?
Sea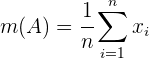
la media de . Entonces, su desviación media es
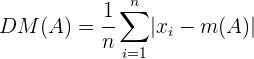
Ahora, notemos que al hacer la modificación del conjunto , obtenemos el conjunto 
cuya media es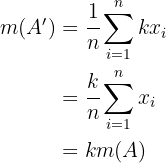
Ahora, la nueva desviación media es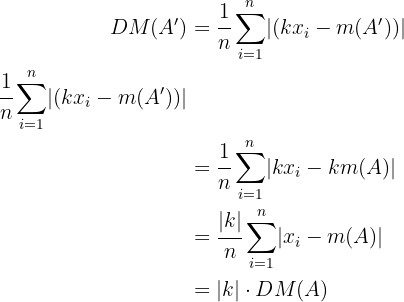 
Es decir, la desviación media de una dilatación de conjunto tiene el efecto de multiplicar por el valor absoluto del coeficiente de dilatación.
Desviación media dada una distribución
Calcular la desviación media de una distribución estadística que viene dada por la siguiente tabla:
 | |
 |  |
 |  |
 |  |
 |  |
 |  |
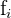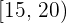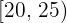Incorporamos otra columna con los productos de las marcas de clase por sus frecuencias absolutas correspondientes y hacemos la sumatoria (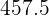
)
Agregamos otra columna con los productos de desviaciones respecto a la media por sus frecuencias absolutas correspondientes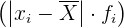 
y calculamos su sumatoria (
)
 |  |  | |
|  |  |  |
|  |  |  |
|  |  |  |
|  |  |  |
|  |  | |
|  |
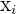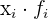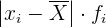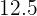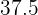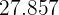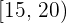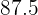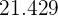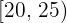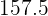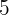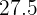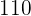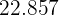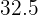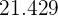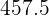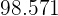Media:
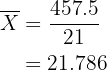
Desviación media:
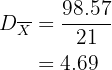
Calcular la desviación media de una distribución estadística que viene dada por la siguiente tabla:
| |
 | |
 |  |
 | |
 |  |
 | |
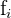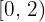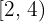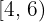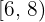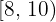Incorporamos otra columna con los productos de las marcas de clase por sus frecuencias absolutas correspondientes y hacemos la sumatoria (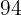
)
Agregamos otra columna con los productos de desviaciones respecto a la media por sus frecuencias absolutas correspondientes 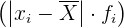y calculamos su sumatoria (
)
| | | |
|  |  |  |
| | |  |
| |  |  |
|  |  |  |
|  |  |  |
|  |
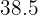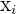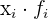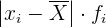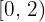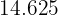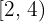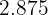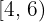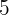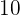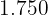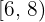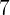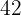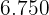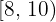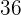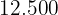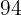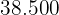Media:
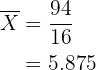
Desviación media:
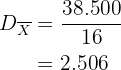
Calcular la desviación media de una distribución estadística que viene dada por la siguiente tabla:
| |
 | |
 | |
 |  |
 | |
 | |
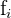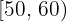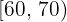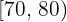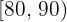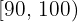Incorporamos otra columna con los productos de las marcas de clase por sus frecuencias absolutas correspondientes y hacemos la sumatoria (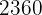
)
Agregamos otra columna con los productos de desviaciones respecto a la media por sus frecuencias absolutas correspondientes 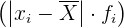y calculamos su sumatoria (
)
| | | |
|  |  |  |
| |  |  |
|  |  |  |
|  |  |  |
|  |  |  |
| |
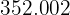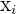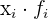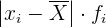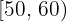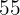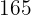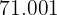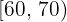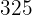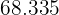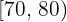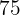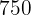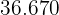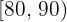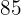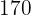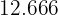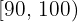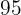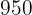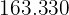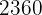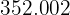Media:
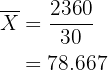
Desviación media:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
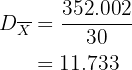
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
4. La tabla registra el ahorro mensual de s/. 100 mensuales. Completa la tabla y contesta.
a) ¿Cuál es la suma de la tercera y cuarta frecuencia absoluta acumulada?
b) ¿Cuántos estudiantes tienen ahorros mayores o iguales que S/. 20, pero menores que S/. 40?
c) ¿Qué porcentaje de estudiantes tienen ahorros menores que S/. 30?
d) ¿A qué intervalo pertenecen los ahorros de la mayoría de los estudiantes?
Lo unico que no me parecio del ejercicio es que al momento de redondear por ejemplo cuando el resultados es .155 asi fue como lo escribi pero me lo marcaba incorrecto, ya que pedia redondear a 16%
Entonces eso complico un poco a la hora de los resultados.
Hola entendemos tu frustración, pero como a veces sucede que algunos libros o maestros piden redondear y otros no, entonces se tomo este criterio que es mas generalizado.
Hola en el ejercicio 1 , punto 2 en la parte de la desviación media creo que hay un 4 de más porque el resultado es parecido me dió 1,52 porque si hacemos el calculo quedan 7,6/5 . Creo que es así. Gracias y buen día.
Hola gracias por visitar nuestra pagina, disculpa pero el artículo que me aparece no los datos que me das, podrías mencionar el titulo del artículo.
deven aver ejersicios de variables estadisticas
Hola te agradecemos la visita a nuestras paginas, vamos a considerar tu recomendación y esperemos pronto tengamos un artículo con el tema que mencionas, para el enriquecimiento de la pagina.