Capítulos
Propiedades fundamentales de los exponentes enteros
1 Cualquier número 
elevado elevado al exponente 1 es el mismo número :
2 Cualquier número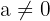 
elevado a la potencia 0 es 1:
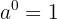
Nota: La expresión 
es una forma indeterminada. Es decir, no está definida.
3 El resultado de elevar cualquier número en una potencia 
par, es positivo. Es decir,
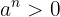
si 
para algún 
.
Nota: esto se puede recordar más fácil viendo la siguiente expresión:
que significa que cualquier número (positivo o negativo) elevado a potencia par da como resultado un número positivo.
4 El resultado de elevar cualquier número en una potencia impar, tiene el mismo signo que . Es decir,
y
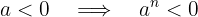
si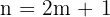 
para algún .
Nota: esta propiedad se puede recordar con la siguiente expresión:
5 Los exponentes negativos cumplen la siguiente propiedad (para ):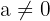
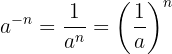
es decir, es igual al recíproco de la base elevado a la potencia positiva.
Ejemplos
Consideremos los siguientes ejemplos:
1 
, 
, 
2 
, 
3 
ya que 6 es un número natural par. Asimismo,
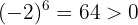
4 
ya que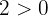 
y 3 es un número impar. Similarmente,
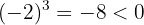
ya que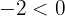 
5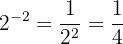 
Exponentes racionales
Definimos las raíces de los números reales de la siguiente manera:
Definición: dado un número 
, la raíces n-ésima de 
es aquél número tal que
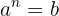
y solemos escribir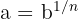 
o 
.
Es por medio de los radicales que se introducen las potencias racionales. Se tienen las siguientes propiedades:
1 Por definición, se tiene que
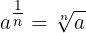
2 También por definición, se tiene que
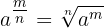
3 Además, se tiene que
Nota: la raíz par de un número negativo no está definida en los números reales. Si estamos trabajando con números reales, entonces podemos decir que esta raíz no existe.
Ejemplos
1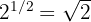 
2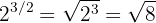 
3 
Leyes de los exponentes con misma base
Las siguientes leyes se cumplen para cualesquiera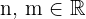 
y cualquiera 
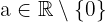. Notemos que, en algunos casos, utilizar 
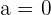nos pueda conducir a indeterminaciones.
1 El producto de dos potencias con la misma base es igual a la base elevada a la suma de los exponentes:
2 La división de dos potencias con la misma base es igual a la base elevada a la resta de los exponentes:
3 Elevar una potencia a otra potencia es igual a elevar la base al producto de los exponentes:
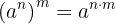
Nota: presta atención a los paréntesis de la expresión anterior. Primero se realiza la operación 
y luego se eleva a la potencia 
. Esto es diferente a la siguiente operación:
y casi nunca son iguales, es decir,
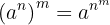
Ejemplos
Considera los siguientes ejemplos:
1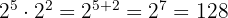 
2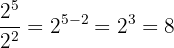 
3 
Operaciones con potencias con el mismo exponente
Las siguientes leyes se cumplen para cualesquiera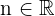 
y cualquiera 
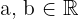y 
.
1 El producto de dos potencias con el mismo exponente es igual al producto de las bases elevados al exponente. Es decir,
2 La división de dos potencias con mismo exponente es igual a la división de las bases elevadas al exponente:
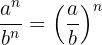
Ejemplos
Considera los siguientes ejemplos:
1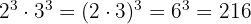 
2 
Ejercicios
Realiza las siguientes potencias:
a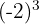
b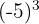
c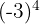
a Notemos que la base es negativa y la potencia es impar. Por lo tanto, el resultado es negativo
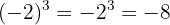
b Notemos que la base es negativa y la potencia es par. Por lo tanto, el resultado es positivo
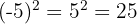
c Tenemos que la base es negativa y la potencia es par. Por lo tanto, el resultado es positivo
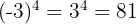
Escribe las siguientes expresiones con potencias positivas:
a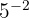
b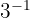
c
Notemos que la potencia es negativa, por lo que la expresión es igual a su recíproco con potencia positiva
a
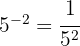
b
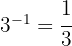
c
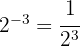
Escribe las siguientes expresiones con radicales:
a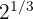
b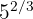
c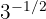
a Notemos que la potencia es fraccionaria. Por lo tanto, empleamos la fórmula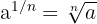 
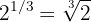
b Notemos que la potencia es fraccionaria. Por lo tanto, empleamos la fórmula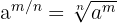 
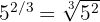
c Notemos que la potencia es fraccionaria y negativa. Por lo tanto, empleamos la fórmula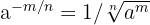 
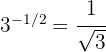
Escribe las siguientes radicales como potencias fraccionarias:
a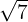
b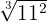
c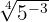
Notemos que para escribir un radical como potencia fraccionaria, empleamos la fórmula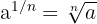
a
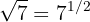
b
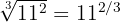
c
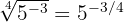
Escribe las siguientes operaciones como una única potencia. Es decir, de la forma 
:
a 
b 
c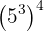 
d 
a Notemos que tenemos multiplicaciones de puros exponentes con la misma base. Por lo tanto, los exponentes se suman:
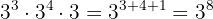
b Ahora tenemos una división entre dos potencias con la misma base. Por tanto, los exponentes se restan:
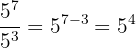
c Tenemos, ahora, una potencia elevada a otra potencia. Por lo tanto, los exponentes se multiplican:
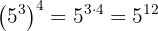
d Notemos que, en este caso, tenemos tres potencias con el mismo exponente. Por tanto, podemos multiplicar las bases:
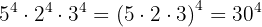
Escribe las siguientes operaciones como una única potencia. Es decir, de la forma :
a 
b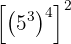 
c 
d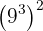 
a El primer caso se trata de una potencia elevada a otra potencia. Así, los exponentes se multiplican:
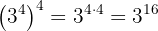
b Este caso es similar al anterior. Tenemos una potencia elevada a otra potencia, y esta elevada a su vez a otra potencia. De este modo, los exponentes se multiplican:
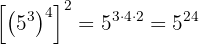
c Tenemos, de nuevo, una potencia elevada a otra potencia:
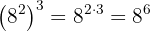
Sin embargo, notemos que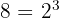 
. Así, podemos simplificar todavía un poco más:
d Tenemos, de nuevo, una potencia elevada a otra potencia. Además, observemos que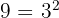 
. Por tanto,
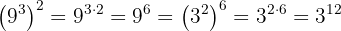
Escribe las siguientes operaciones como una única potencia. Es decir, de la forma :
a 
b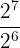 
c 
d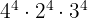 
a Tenemos una multiplicación de potencias con la misma base. Por tanto, se suman los exponentes,
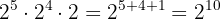
b Ahora tenemos una división entre potencias con la misma base, por lo que los exponentes se restarán:
c Observemos que tenemos una potencia elevada a otra potencia. De este modo, los exponentes se suman,
d Tenemos, ahora, multiplicación de potencias con el mismo exponente. Por tanto, podemos multiplicar las bases,
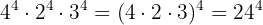
Escribe las siguientes operaciones como una única potencia. Es decir, de la forma :
a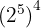 
b 
c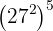 
d 
a Tenemos una potencia elevada a otra potencia. Por tanto, los exponentes se multiplican
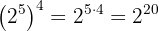
b Observemos que tenemos una potencia elevada al exponente 0. Como
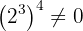
entonces podemos concluir que
c Tenemos una potencia elevada a otra potencia. Asimismo,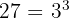 
d De nuevo tenemos una potencia elevada a otra potencia. Además,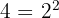 
:
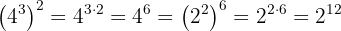
Realiza por completo las siguientes operaciones con potencias:
a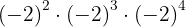 
b 
c 
d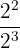 
a Observemos que tenemos multiplicación de potencias con la misma base. Por tanto, los exponentes se suman:
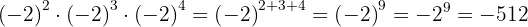
donde sacamos el signo ya que estamos elevando a una potencia impar.
b Al igual que en el caso anterior, tenemos multiplicación de potencias con la misma base,
De nuevo sacamos el signo ya que estamos elevando a una potencia impar.
c Una vez más, tenemos multiplicación de potencias con la misma base:
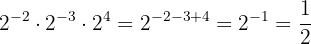
d Ahora tenemos una división de potencias con la misma base. Así, los exponentes se restan:
Realiza por completo las siguientes operaciones con potencias:
a 
b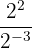 
c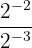 
a Tenemos división de potencias con la misma base:
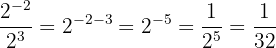
b De nuevo, tenemos división de potencias con la misma base:
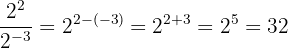
c Una vez más, se trata de una división de potencias con la misma base:
Calcula las siguientes potencias:
a 
b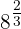 
c 
d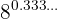 
Recordemos que los exponentes fraccionales implican raíces.
a Esta expresión se puede escribir como
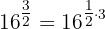
Luego, utilizando la propiedad de la multiplicación de exponentes,
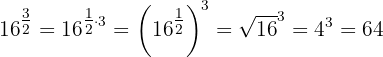
b Podemos escribir la expresión como
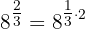
Si utilizamos la propieda de multiplicación de exponentes:
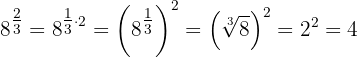
c Notemos que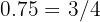 
. Por tanto,
Luego,
d Ahora el exponente es 
. Así
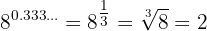
Simplifica la siguiente expresión
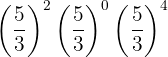
Debemos simplificar la siguiente expresión, la cual denotaremos como 
:
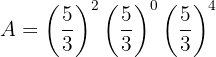
Empezamos notando que cualquier número elevado al exponente 0 es 1. Además, podemos utilizar la propiedad de multiplicación de exponentes:
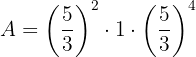
Después sumamos los exponentes que tengan la misma base:
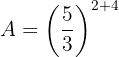
es decir,
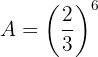
Simplifica la siguiente expresión
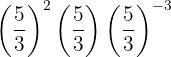
Debemos simplificar la siguiente expresión, la cual denotaremos como :
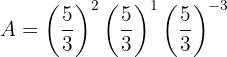
Podemos utilizar la propiedad de multiplicación de exponentes:
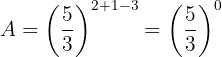
Aplicamos la propiedad de que cualquier número elevado al exponente cero es uno:
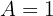
Simplifica la siguiente expresión
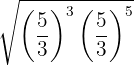
Debemos simplificar la siguiente expresión, la cual denotaremos como :
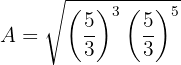
Podemos utilizar la propiedad de multiplicación de exponentes:
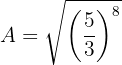
Escribimos en forma de potencia fraccionaria:
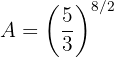
es decir,
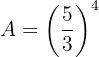
Simplifica la siguiente expresión
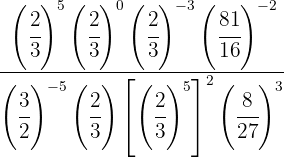
Debemos simplificar la siguiente expresión, la cual denotaremos como :
Empezamos notando que cualquier número elevado al exponente 0 es 1 (en el numerador). Además, en el denominador podemos utilizar la propiedad de multiplicación de exponentes:
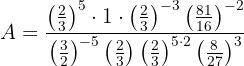
Después sumamos los exponentes que tengan la misma base:
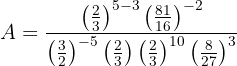
es decir,
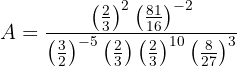
Convertimos aquellos exponentes que estén elevados a exponente negativo, utilizando el recíproco de la base:
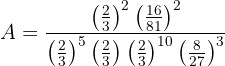
De nuevo, sumamos/restamos los índices de aquellas potencias con la misma base:
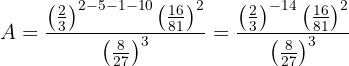
Ahora notemos que
y que
Por lo tanto, la expresión se convierte en
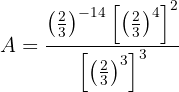
Utilizamos de nuevo la propiedad de multiplicación de exponentes:
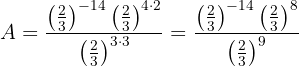
Sumamos/restamos los exponentes:
Por lo tanto, tenemos que
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Este tipo de ejercicios no solo fortalecen el razonamiento algebraico, sino que también entrenan tu capacidad para explicar procesos paso a paso, algo que tú haces muy bien en tus presentaciones. Además, el uso de Ruffini y el teorema del resto te permite abordar polinomios complejos con elegancia y lógica, algo muy útil en programación y algoritmos también.
Utilizar el teorema del resto, la regla de ruffini y la formula general para ecuaciones de segundo grado
Escribo y elijo bien las respuestas y me aparece el setenta porciento, no entiendo porque si todas me quedan bien.
Hola te agradecemos por visitar nuestra pagina, en cuanto a lo que pasa con los resultados del cuestionario, se supone que la pagina te da las respuestas de los ejercicios y allí puedes ver cual ejercicio tiene el error, podrías por favor indicárnoslo para rectificarlo.
– 2 no es raíz del último polunomio
Hola gracias por tus observaciones, podrías hacernos el favor de mencionar el número del ejercicio para poder rectificarlo, seria de gran ayuda.
(14m³×+21m²)÷(-7)