Ejemplos paso a paso de la regla de Ruffini
Ejemplo: Dividir: 
1 Si el polinomio no es completo, lo completamos añadiendo los términos que faltan con ceros
2Colocamos los coeficientes del dividendo en una línea
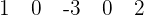
3Abajo a la izquierda colocamos el opuesto del término independendiente del divisor: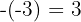 
4Trazamos una raya y bajamos el primer coeficiente 
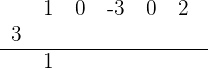
5Multiplicamos ese coeficiente por el divisor 
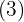y lo colocamos debajo del siguiente término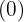 
6Sumamos los dos coeficientes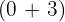 
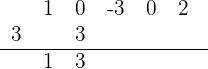
7Repetimos el proceso anterior 
Volvemos a repetir el proceso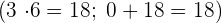 
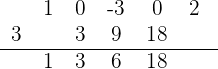
Volvemos a repetir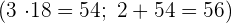 
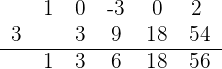
8El último número obtenido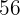 
, es el resto
9El cociente es un polinomio de grado inferior en una unidad al dividendo y cuyos coeficientes son los que hemos obtenido
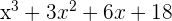
Ejemplo: Dividir por la regla de Ruffini: 
1 Si el polinomio no es completo, lo completamos añadiendo los términos que faltan con ceros
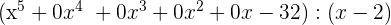
2Colocamos los coeficientes del dividendo en una línea
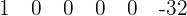
3Abajo a la izquierda colocamos el opuesto del término independendiente del divisor: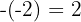 
4Trazamos una raya y bajamos el primer coeficiente
5Multiplicamos ese coeficiente por el divisor 
y lo colocamos debajo del siguiente término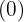
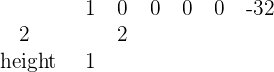
6Sumamos los dos coeficientes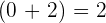 
7 Repetimos el proceso anterior 
Volvemos a repetir el proceso 
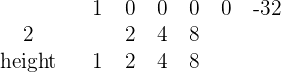
Volvemos a repetir 
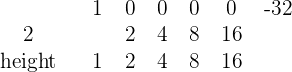
Volvemos a repetir 
8El último número obtenido 
, es el resto
9El cociente es un polinomio de grado inferior en una unidad al dividendo y cuyos coeficientes son los que hemos obtenido
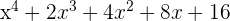
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el cálculo con polinomios creo que la 4 estaba mal
Hola revise el ejercicio y no encontré el error, pero al principio me confundí pues la solución esta arriba del número, no se si te paso a ti, si no fue así, podrías señalármelo por favor.
HAY MUCHOS ERRORES
Miren sus soluciones a los problemas, los errores en la resolucion de sus propios problemas son DEMACIADOS.
Un ejemplo en calculos con polinomios
(x²+2)² (a+b)²=a²+2ab+b²
(x²)²+2(x²)(2)+2²
resultado real= x⁴+4x²+4
el suyo es= x⁴+2x²+4
Los invito a realizar su chequeo ya que confunde y desmotiva el uso de la pagina a la gran mayoria que estamos aprendiendo.
Hola te agradecemos tus comentarios, el error que mencionas ya se corrigió, si encuentras algún otro con gusto te atenderemos.
Este tipo de ejercicios no solo fortalecen el razonamiento algebraico, sino que también entrenan tu capacidad para explicar procesos paso a paso, algo que tú haces muy bien en tus presentaciones. Además, el uso de Ruffini y el teorema del resto te permite abordar polinomios complejos con elegancia y lógica, algo muy útil en programación y algoritmos también.
Utilizar el teorema del resto, la regla de ruffini y la formula general para ecuaciones de segundo grado